深層学習ニューラル ネットワークのトレーニングに一般的に使用される 5 つの損失関数

トレーニング中のニューラル ネットワークの最適化では、まずモデルの現在の状態の誤差を推定します。次に、次の評価の誤差を減らすために、誤差を表現できる関数を使用する必要があります。重みを更新するこの関数を損失関数と呼びます。

#損失関数の選択は、ニューラル ネットワーク モデルが例から学習する特定の予測モデリング問題 (分類や回帰など) に関連します。この記事では、次のような一般的に使用される損失関数をいくつか紹介します。

• 回帰モデルの平均二乗誤差損失
• 二項分類モデルのクロス エントロピーとヒンジ損失

回帰モデルの損失関数

回帰予測モデルは主に連続値を予測するために使用されます。そこで、scikit-learn の make_regression() 関数を使用してシミュレートされたデータを生成し、このデータを使用して回帰モデルを構築します。

20 個の入力特徴を生成します。そのうち 10 個は意味がありますが、10 個は問題とは無関係です。

そして、1,000 個の例をランダムに生成します。また、ランダム シードを指定すると、コードを実行するたびに同じ 1,000 個のサンプルが生成されます。

実数値の入力変数と出力変数を適切な範囲にスケーリングすると、多くの場合、ニューラル ネットワークのパフォーマンスが向上します。したがって、データを標準化する必要があります。

StandardScaler can also be found in the scikit-learn library. 問題を単純化するために、トレーニング セットとテスト セットに分割する前にすべてのデータをスケーリングします。

次に、トレーニング セットと検証セットを均等に分割します。

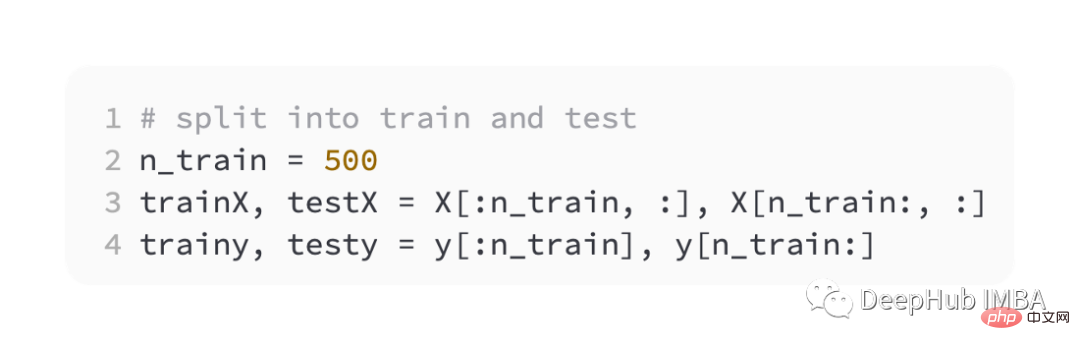
さまざまな損失関数を導入するために、小さなマルチを開発します。 - レイヤーパーセプトロン (MLP) モデル。

問題定義によれば、モデルを通過する入力として 20 個の特徴があります。予測には実際の値が必要なため、出力層にはノードが含まれます。

最適化には SGD を使用し、学習率は 0.01、運動量は 0.9 で、どちらも妥当なデフォルト値です。トレーニングは 100 エポックで実行され、各段階の終了時にテスト セットが評価され、学習曲線がプロットされます。

モデルが完成したら、損失関数を導入できます。

MSE

最も一般的に使用される回帰問題は平均値です。二乗誤差損失 (MSE)。これは、ターゲット変数の分布がガウス分布である場合の最尤推定における好ましい損失関数です。したがって、より適切な理由がある場合にのみ、他の損失関数に変更する必要があります。

Keras でモデルをコンパイルするときに損失関数として「mse」または「mean_squared_error」が指定されている場合、平均二乗誤差損失関数が使用されます。

以下のコードは、上記の回帰問題の完全な例です。

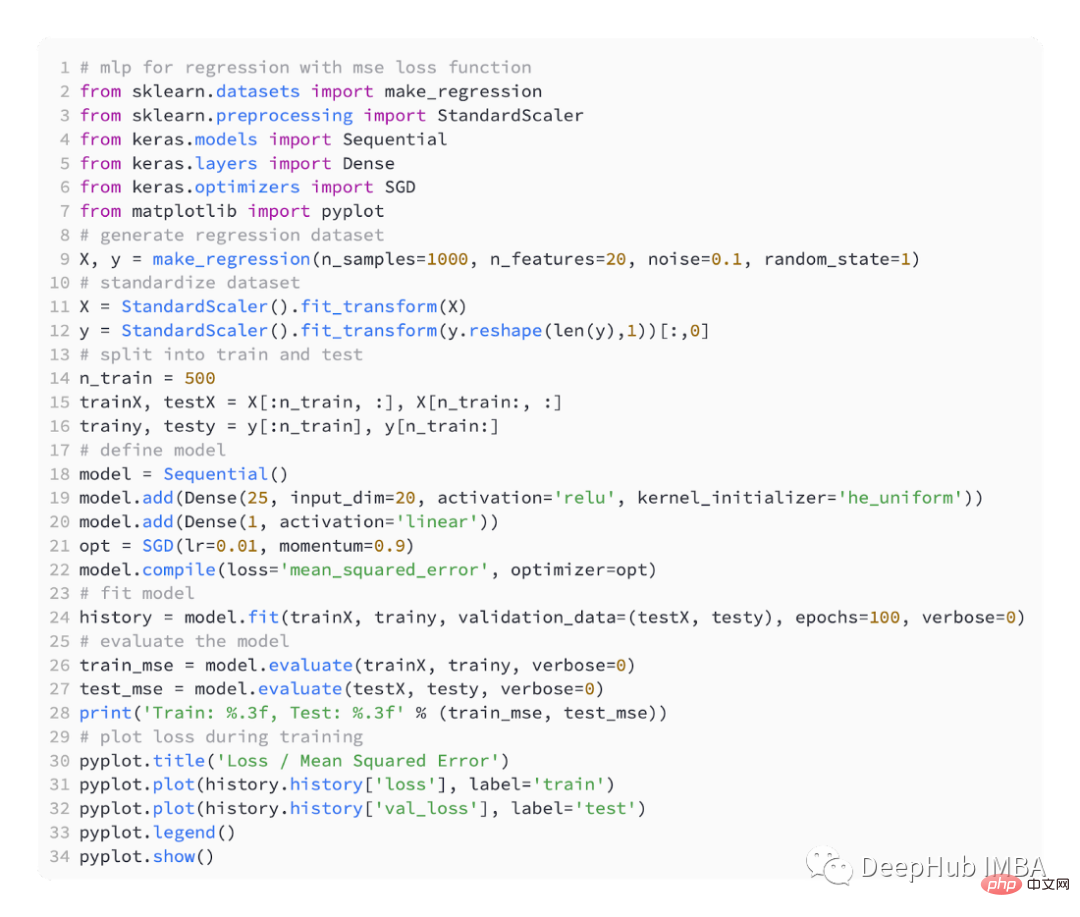
例を実行する最初のステップでは、モデルのトレーニング データ セットとテスト データ セットの平均二乗誤差が出力されます。小数点以下 3 桁が保持されるため、次のようになります。 0.000

以下の図からわかるように、モデルは非常に早く収束し、トレーニングとテストのパフォーマンスは変化しません。モデルのパフォーマンスと収束特性によっては、回帰問題には平均二乗誤差が適しています。

#MSLE

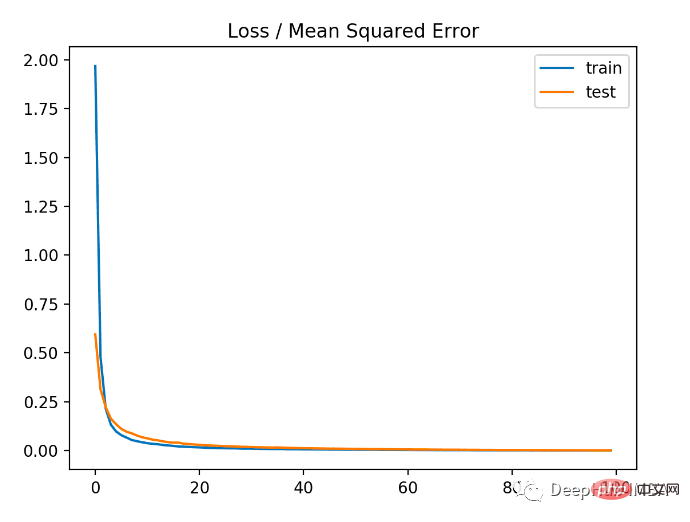
広範囲の値を使用する回帰問題では、予測時に平均二乗誤差ほどモデルにペナルティを与えることは望ましくない場合があります。大きな値。したがって、平均二乗誤差は、最初に各予測値の自然対数を計算することで計算できます。この損失は MSLE (平均二乗対数誤差) と呼ばれます。

予測値に大きな差があった場合のペナルティ効果を緩和する効果があります。モデルがスケーリングされていない量を直接予測する場合、これはより適切な損失測定となる可能性があります。

keras の損失関数として「mean_squared_logarithmic_error」を使用する

以下の例は、MSLE 損失関数を使用した完全なコードです。

モデルの MSE は、トレーニング データセットとテスト データセットの両方でわずかに悪くなります。これは、ターゲット変数の分布が標準のガウス分布であるためです。これは、損失関数がこの問題にはあまり適していない可能性があることを意味します。

下の図は、各トレーニング ラウンドの比較を示しています。MSE は良好に収束していますが、ラウンド 20 から変化に向けて減少し、上昇し始めるため、MSE は過学習している可能性があります。

MAE

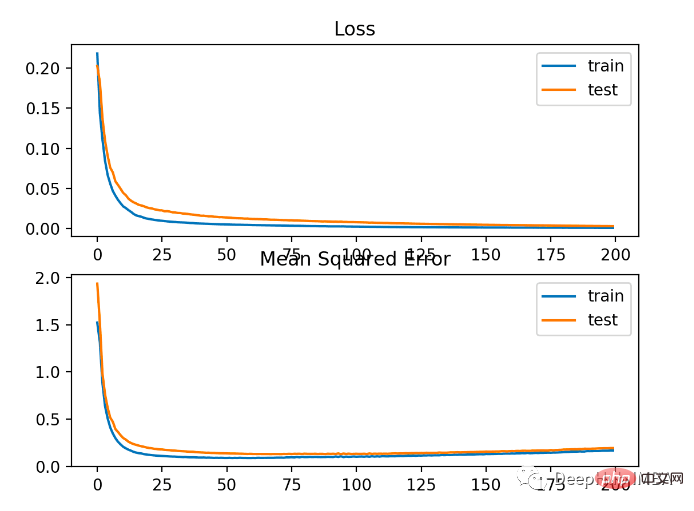
回帰問題によっては、ターゲット変数の分布は主にガウス分布になりますが、大きな値などの外れ値が含まれる場合があります。平均値または小さい値から大きく離れています。

この場合、平均絶対誤差または MAE 損失は、外れ値に対してより堅牢であるため、適切な損失関数です。実際の値と予測値の間の絶対差を考慮して、平均として計算されます。

「mean_absolute_error」損失関数の使用

これは MAE を使用した完全なコードです

結果は次のとおりです。

下の図からわかるように、MAE は確かに収束しましたが、プロセスに凹凸があります。ターゲット変数が大きな外れ値のないガウス関数であるため、MAE もこの場合にはあまり適していません。

バイナリ分類の損失関数

バイナリ分類問題は、予測モデリング問題の 2 つのラベルのうちの 1 つです。この問題は、最初または 2 番目のクラスの値を 0 または 1 として予測するものとして定義され、一般にクラス値 1 に属する確率を予測するものとして実装されます。

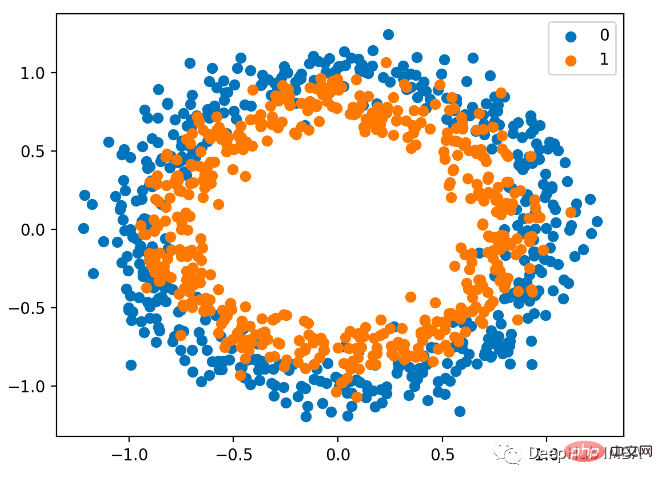
データの生成にも sklearn を使用します。ここでは円の問題を使用します。これには 2 次元平面と 2 つの同心円があります。外側の円上の点はクラス 0 に属し、内側の円上の点はクラス 0 に属します。クラス1に属します。学習をより困難にするために、サンプルに統計的なノイズも追加します。サンプルサイズは 1000 で、10% の統計ノイズが追加されます。

#データセットの散布図は、モデル化している問題を理解するのに役立ちます。以下に完全な例を示します。

#散布図は次のとおりです。ここで、入力変数は点の位置を決定し、色はクラス値です。 0 は青、1 はオレンジです。

ここではまだ半分がトレーニング用で、半分がテスト用です。

まだ単純な MLP モデルを定義しています

学習率 0.01、運動量 0.99 の SGD 最適化を使用します。

モデルは 200 ラウンドのフィッティングでトレーニングされ、モデルのパフォーマンスは損失と精度に基づいて評価されます。

BCE

BCE は、バイナリ分類問題を解くために使用されるデフォルトの損失関数です。最尤推論フレームワークでは、これが損失関数として選択されます。タイプ 1 の予測の場合、クロスエントロピーは、実際の確率分布と予測された確率分布の間の平均差を要約するスコアを計算します。

Keras モデルをコンパイルするときに、損失関数として binary_crossentropy を指定できます。

#クラス 1 の確率を予測するには、出力層にノードと「シグモイド」アクティベーションが含まれている必要があります。

以下は完全なコードです:

モデルはテスト データ セット内で問題を比較的よく学習します。正解率は83％、正解率は85％です。スコア間にはある程度の重複があり、モデルが過学習でも過小学習でもないことを示しています。

下の写真に示すように、トレーニング効果は非常に優れています。確率分布間の誤差は連続的であるため、損失プロットは滑らかですが、トレーニング セットとテスト セット内の例は正しいか不正確であるかしか予測できず、提供される情報の粒度が低いため、精度線プロットには凹凸が表示されます。

ヒンジ

サポート ベクター マシン (SVM) モデルは、クロス エントロピーの代わりにヒンジ損失関数を使用して、バイナリ分類問題を解決します。

ターゲット値はセット [-1, 1] 内にあり、二項分類での使用を目的としています。実際のクラス値と予測されたクラス値の符号が異なる場合、ヒンジのエラーは大きくなります。二項分類問題ではクロスエントロピーよりも優れている場合があります。

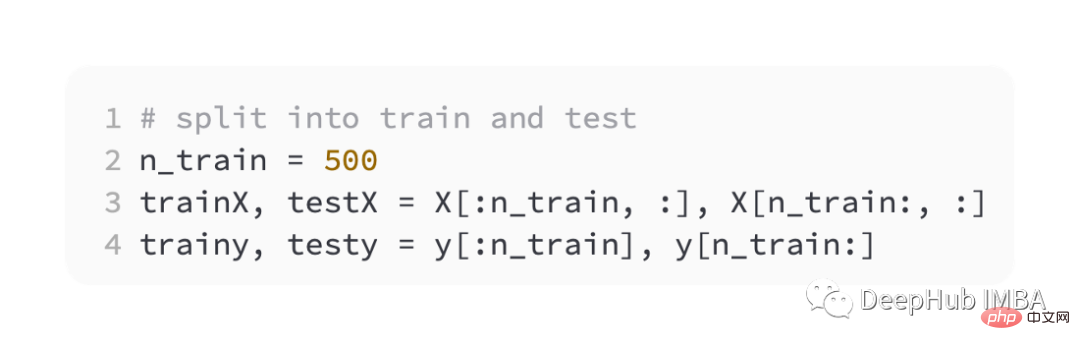
最初のステップとして、ターゲット変数の値をセット {-1, 1} に変更する必要があります。

keras では「ヒンジ」と呼ばれます。

ネットワークの出力層では、-1 から 1 までの単一の値を出力するには、tanh 活性化関数を持つ単一ノードを使用する必要があります。

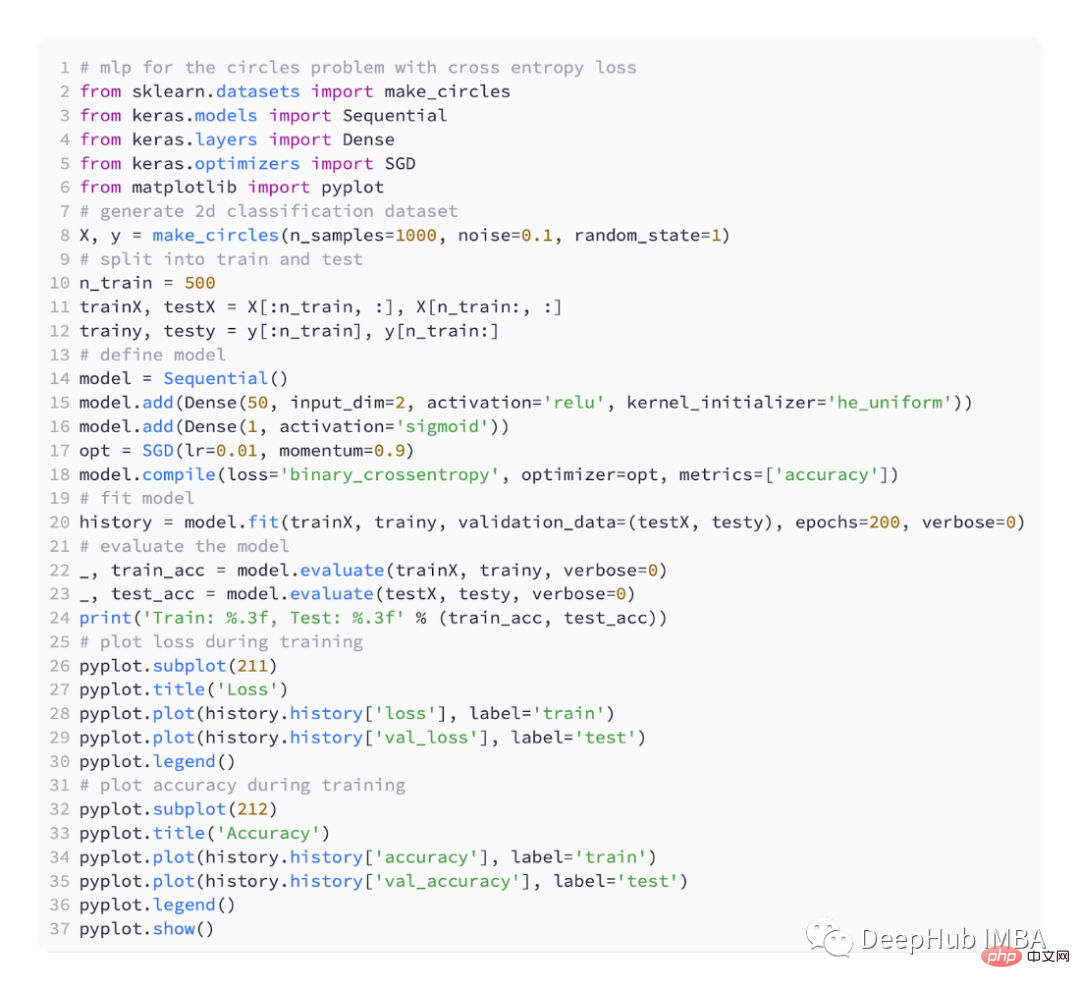
以下は完全なコードです:

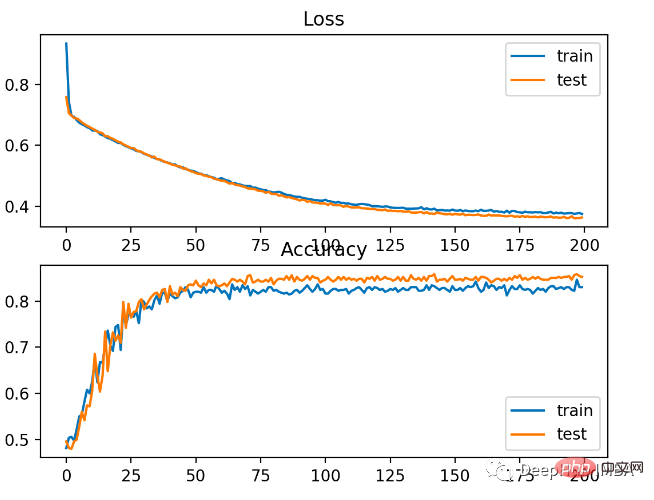
トレーニング セットとテスト セットでは、クロス エントロピーよりもパフォーマンスがわずかに劣ります。精度は 80% 未満です。

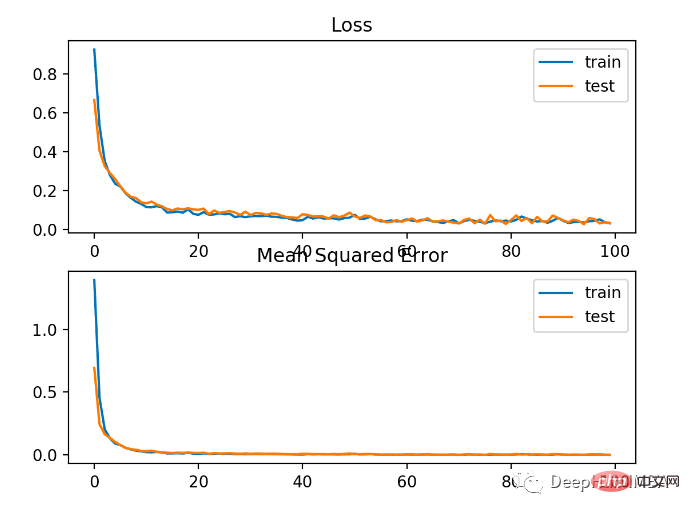
#以下の図からわかるように、モデルは収束しており、分類精度グラフからも収束していることがわかります。

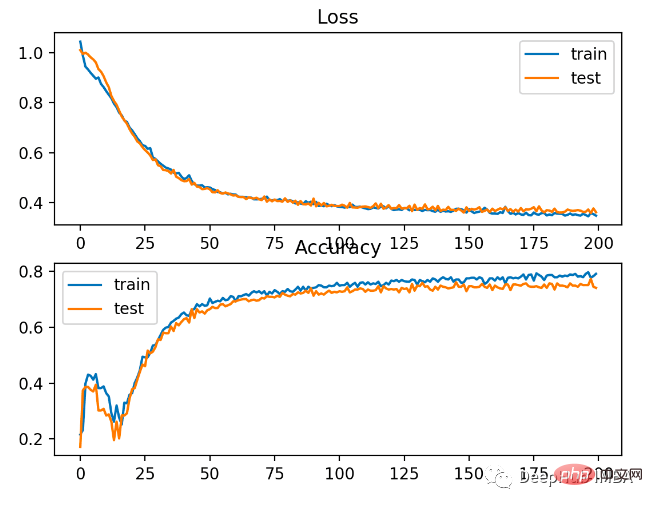
この問題には BCE の方が適していることがわかります。考えられる理由は、いくつかのノイズ ポイントがあるためです。

以上が深層学習ニューラル ネットワークのトレーニングに一般的に使用される 5 つの損失関数の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。