機械学習で一般的に使用される 10 の距離測定方法

距離メトリックは、k 最近傍法、サポート ベクター マシン、k 平均法クラスタリングなどの教師あり学習アルゴリズムと教師なし学習アルゴリズムの基礎です。

距離メトリックの選択は機械学習の結果に影響するため、どのメトリックが問題に最適であるかを検討することが重要です。したがって、どの測定方法を使用するかを決定する際には注意が必要です。しかし、決定を下す前に、距離測定がどのように機能するのか、またどのような測定値を選択できるのかを理解する必要があります。

この記事では、一般的に使用される距離測定方法、その仕組み、Python での計算方法、およびそれらを使用する場合について簡単に紹介します。これにより、知識と理解が深まり、機械学習のアルゴリズムと結果が向上します。

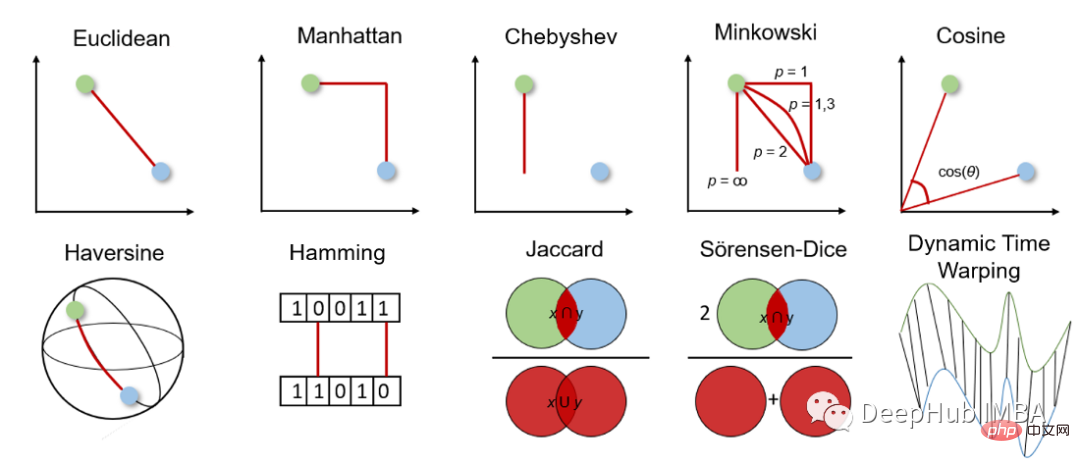
さまざまな距離測定について詳しく説明する前に、まず距離測定がどのように機能するか、および適切な測定を選択する方法についての一般的な概念を理解する必要があります。

距離メトリックは、特定の問題空間内の 2 つのオブジェクト (つまり、データセット内のフィーチャ) 間の差を計算するために使用されます。この距離は、特徴間の類似性を判断するために使用できます。距離が小さいほど、特徴は類似しています。

距離測定には、幾何学的距離測定と統計的距離測定があり、データの種類に応じてどちらの距離測定を選択するかが異なります。特徴はさまざまなデータ型 (実数値、ブール値、カテゴリ値など) である場合があり、データは多次元である場合や地理空間データで構成されている場合があります。

幾何距離測定

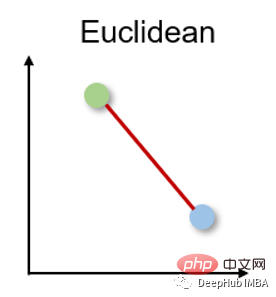
1. ユークリッド距離ユークリッド距離

ユークリッド距離は、2 つの実数値ベクトル間の最短距離を測定します。直感的で使いやすく、多くのユースケースで良好な結果が得られるため、最も一般的に使用される距離メトリックであり、多くのアプリケーションのデフォルトの距離メトリックです。

ユークリッド距離は l2 ノルムとも呼ばれ、その計算方法は次のとおりです。

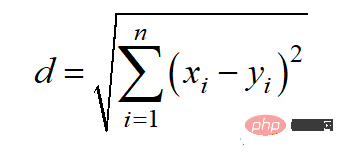
Python コードは次のとおりです。続く

from scipy.spatial import distance
 distance.euclidean(vector_1, vector_2)

ユークリッド距離には 2 つの主な欠点があります。まず、距離測定は 2D または 3D 空間よりも高次元のデータでは機能しません。第 2 に、特徴を正規化および/または正規化しないと、距離が単位によって歪む可能性があります。

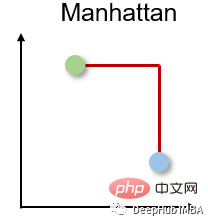
2. マンハッタン距離

マンハッタン距離は、2 つの実数値ベクトル間の距離が計算上、人間は直角にしか移動できないという事実に基づいているため、タクシー距離または市街地区距離とも呼ばれます。 。この距離測定は、真のパスを取得できるように、離散属性とバイナリ属性によく使用されます。

マンハッタン距離は l1 ノルムに基づいており、計算式は次のとおりです。

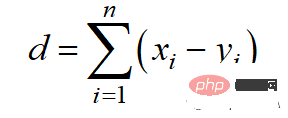
Python コードは次のとおりです。以下のように

from scipy.spatial import distance
 distance.cityblock(vector_1, vector_2)

マンハッタンからの距離には、2 つの大きな欠点があります。これは、高次元空間におけるユークリッド距離ほど直感的ではなく、可能な最短経路を示すものでもありません。これは問題ではないかもしれませんが、これが最短距離ではないことに注意する必要があります。

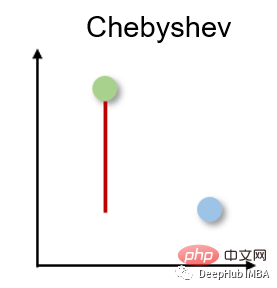
3. チェビシェフ距離 チェビシェフ距離

チェビシェフ距離は、2 つの実数値ベクトル間の任意の次元における最大距離であるため、チェッカーボード距離とも呼ばれます。これは倉庫物流でよく使用され、最長の経路によってある地点から別の地点に移動するのに必要な時間が決まります。

チェビシェフ距離は l-無限ノルムによって計算されます:

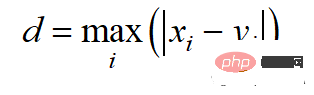
Python コードは次のとおりです

from scipy.spatial import distance
 distance.chebyshev(vector_1, vector_2)

チェビシェフ距離は非常に特殊な使用例しかないため、めったに使用されません。

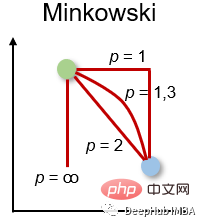
4. ミンコフスキー距離 ミンコフスキー距離

ミンコフスキー距離は、上記の距離測定の一般化された形式です。高い柔軟性を提供しながら、同じユースケースに使用できます。 p 値を選択して、最も適切な距離の尺度を見つけることができます。

#ミンコフスキー距離の計算方法は次のとおりです。

Python コードは次のとおりです。

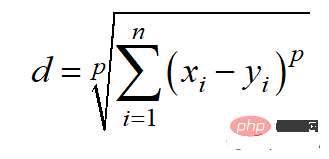
from scipy.spatial import distance
 distance.minkowski(vector_1, vector_2, p)

##なぜなら、ミンコフスキー距離は異なる距離計量を表し、高次元空間の問題や特徴単位への依存など、それらと同じ主な欠点があるからです。さらに、p 値の柔軟性も欠点となる可能性があります。正しい p 値を見つけるには複数の計算が必要となるため、計算効率が低下する可能性があります。

5. コサイン類似度と距離 コサイン類似度

コサイン類似度は方向の尺度であり、そのサイズは 2 つのベクトル間のコサインによって決定され、ベクトルのサイズは無視されます。コサイン類似度は、レコメンダー システムやテキスト分析など、データのサイズが重要ではない高次元でよく使用されます。

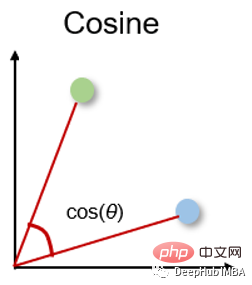
余弦相似度可以介于-1(相反方向)和1(相同方向)之间，计算方法为:

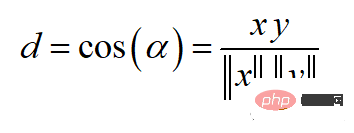
余弦相似度常用于范围在0到1之间的正空间中。余弦距离就是用1减去余弦相似度，位于0(相似值)和1(不同值)之间。

Python代码如下

from scipy.spatial import distance
 distance.cosine(vector_1, vector_2)

余弦距离的主要缺点是它不考虑大小而只考虑向量的方向。因此，没有充分考虑到值的差异。

6、半正矢距离 Haversine distance

半正矢距离测量的是球面上两点之间的最短距离。因此常用于导航，其中经度和纬度和曲率对计算都有影响。

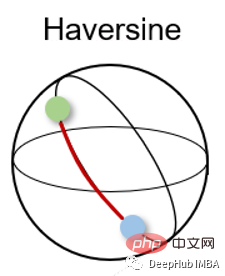
半正矢距离的公式如下：

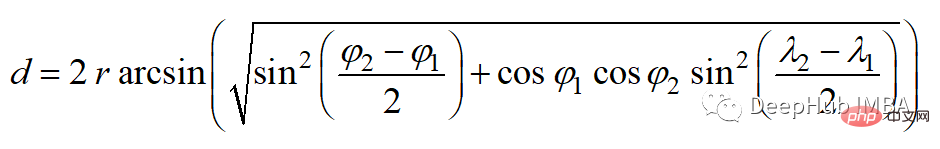
其中r为球面半径，φ和λ为经度和纬度。

Python代码如下

from sklearn.metrics.pairwise import haversine_distances
 haversine_distances([vector_1, vector_2])

半正矢距离的主要缺点是假设是一个球体，而这种情况很少出现。

7、汉明距离

汉明距离衡量两个二进制向量或字符串之间的差异。

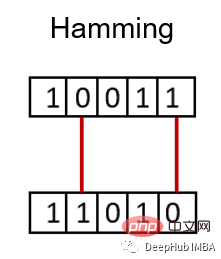
对向量按元素进行比较，并对差异的数量进行平均。如果两个向量相同，得到的距离是0之间，如果两个向量完全不同，得到的距离是1。

Python代码如下

from scipy.spatial import distance
 distance.hamming(vector_1, vector_2)

汉明距离有两个主要缺点。距离测量只能比较相同长度的向量，它不能给出差异的大小。所以当差异的大小很重要时，不建议使用汉明距离。

统计距离测量

统计距离测量可用于假设检验、拟合优度检验、分类任务或异常值检测。

8、杰卡德指数和距离 Jaccard Index

Jaccard指数用于确定两个样本集之间的相似性。它反映了与整个数据集相比存在多少一对一匹配。Jaccard指数通常用于二进制数据比如图像识别的深度学习模型的预测与标记数据进行比较，或者根据单词的重叠来比较文档中的文本模式。

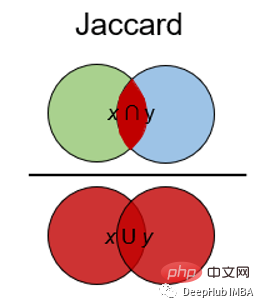
Jaccard距离的计算方法为:

Python代码如下

from scipy.spatial import distance
 distance.jaccard(vector_1, vector_2)

Jaccard指数和距离的主要缺点是，它受到数据规模的强烈影响，即每个项目的权重与数据集的规模成反比。

9、Sorensen-Dice指数

Sörensen-Dice指数类似于Jaccard指数，它可以衡量的是样本集的相似性和多样性。该指数更直观，因为它计算重叠的百分比。Sörensen-Dice索引常用于图像分割和文本相似度分析。

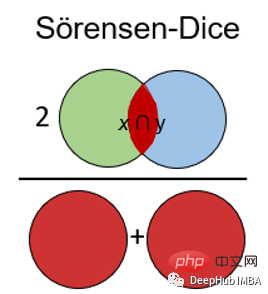
计算公式如下：

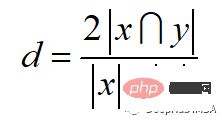
Python代码如下

from scipy.spatial import distance
 distance.dice(vector_1, vector_2)

它的主要缺点也是受数据集大小的影响很大。

10、动态时间规整 Dynamic Time Warping

动态时间规整是测量两个不同长度时间序列之间距离的一种重要方法。可以用于所有时间序列数据的用例，如语音识别或异常检测。

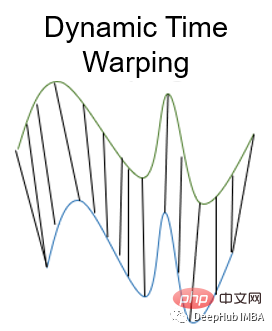
为什么我们需要一个为时间序列进行距离测量的度量呢？如果时间序列长度不同或失真，则上述面说到的其他距离测量无法确定良好的相似性。比如欧几里得距离计算每个时间步长的两个时间序列之间的距离。但是如果两个时间序列的形状相同但在时间上发生了偏移，那么尽管时间序列非常相似，但欧几里得距离会表现出很大的差异。

动态时间规整通过使用多对一或一对多映射来最小化两个时间序列之间的总距离来避免这个问题。当搜索最佳对齐时，这会产生更直观的相似性度量。通过动态规划找到一条弯曲的路径最小化距离，该路径必须满足以下条件：

• 边界条件:弯曲路径在两个时间序列的起始点和结束点开始和结束
• 单调性条件:保持点的时间顺序，避免时间倒流
• 连续条件:路径转换限制在相邻的时间点上，避免时间跳跃
• 整经窗口条件(可选):允许的点落入给定宽度的整经窗口
• 坡度条件(可选):限制弯曲路径坡度，避免极端运动

我们可以使用 Python 中的 fastdtw 包：

from scipy.spatial.distance import euclidean
 from fastdtw import fastdtw
 
 distance, path = fastdtw(timeseries_1, timeseries_2, dist=euclidean)

动态时间规整的一个主要缺点是与其他距离测量方法相比，它的计算工作量相对较高。

总结

在这篇文章中，简要介绍了十种常用的距离测量方法。本文中已经展示了它们是如何工作的，如何在Python中实现它们，以及经常使用它们解决什么问题。如果你认为我错过了一个重要的距离测量，请留言告诉我。

以上が機械学習で一般的に使用される 10 の距離測定方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。