Python 仮想マシンにおける整数の実装原理は何ですか?

データ構造

cpython内部のint型の実装データ構造は次のとおりです:

typedef struct _longobject PyLongObject;
struct _longobject {
    PyObject_VAR_HEAD
    digit ob_digit[1];
};
#define PyObject_VAR_HEAD      PyVarObject ob_base;
typedef struct {
    PyObject ob_base;
    Py_ssize_t ob_size; /* Number of items in variable part */
} PyVarObject;
typedef struct _object {
    _PyObject_HEAD_EXTRA
    Py_ssize_t ob_refcnt;
    struct _typeobject *ob_type;
} PyObject;

上記のデータ構造をグラフィカルに表すと以下のようになります:

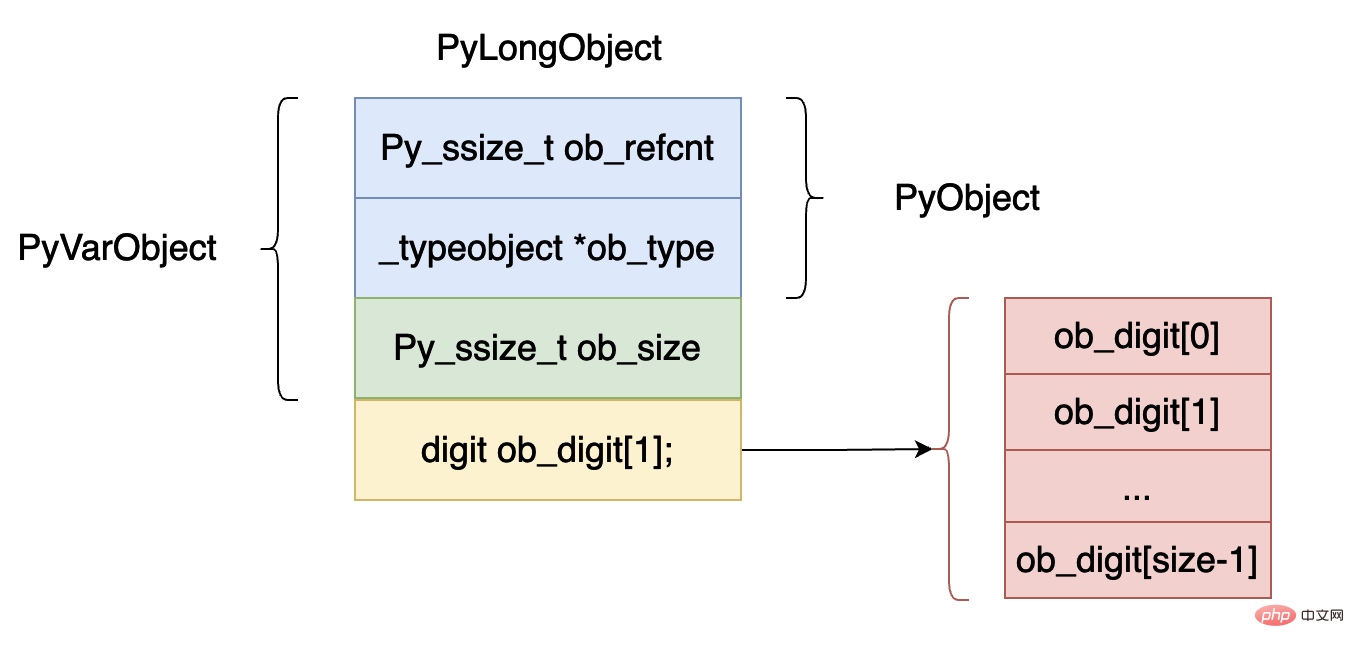
• ob_refcnt は、オブジェクトの参照カウントの数を表します。これは、ガベージ コレクションに非常に役立ちます。後で、仮想マシンのガベージ コレクション部分を詳しく分析します。

• ob_type, は、このオブジェクトのデータ型を示します。Python では、データのデータ型を判断する必要がある場合があります。たとえば、isinstance と type の 2 つのキーワードは次のようになります。中古フィールドです。

• ob_size、このフィールドは、この整数オブジェクト配列 ob_digit に要素がいくつあるかを示します。

• 数字型は実際には、32 ビット整数データを表す uint32_t 型のマクロ定義です。

PyLongObject フィールドのセマンティクスの詳細な分析

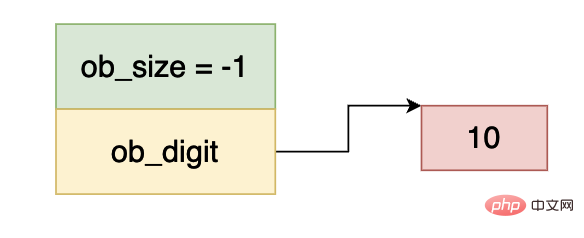
まず、Python では整数がオーバーフローしないことがわかっており、これが PyLongObject が配列を使用する理由です。 cpython の内部実装では、整数には 0、正の数、負の数が含まれますが、これに関して cpython では次のような規定があります。 ob_size 0 より大きい場合は正の数が格納され、ob_size が 0 より小さい場合は負の数が格納されます。

• ob_digit、整数の絶対値を格納します。前に述べたように、ob_digital は 32 ビット データですが、オーバーフローの問題を避けるため、cpython では最初の 30 ビットのみが内部で使用されます。

• 上記のルールを詳しく理解するために、いくつかの例を使用してみましょう:

上の図では、ob_size は 0 より大きくなっています。 , この数値が正の数値であり、ob_digit が int32 データを指していることを示します。数値の値は 10 に等しいため、上記の数値は整数 10 を表します。

同様に、ob_size は 0 未満で、ob_digit は 10 に等しいため、上の図のデータは -10 を表します。

上記は、ob_digit 配列の長さが 2 である例です。上記で表されるデータは次のとおりです:

1⋅2

0

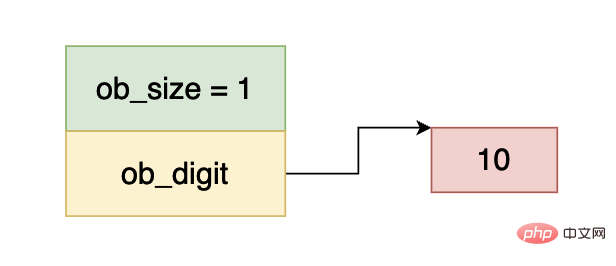
1⋅2

1

1⋅2² ... 1⋅2²⁹ 0⋅2³⁰ 0⋅2 ³¹ 1⋅2³²各配列要素の最初の 30 ビットのみを使用するため、2 番目の整数データは 230 に対応し、誰でも理解できます。上記の結果に基づいて計算プロセス全体を実行します。

上記は非常に簡単です:

−(1⋅2

0

1⋅2

1

1⋅2² ... 1⋅2²⁹ 0⋅2³⁰ 0⋅2³¹ 1⋅2 ³² )小さな整数プール一般的に使用される整数を頻繁に作成することを避け、プログラムの実行を高速化するために、必要に応じて、一般的に使用される整数を最初にキャッシュできます。このデータを返すだけです。直接。 cpython の関連コードは次のとおりです: (小さい整数プール内のキャッシュされたデータの間隔は [-5, 256])

#define NSMALLPOSINTS           257
#define NSMALLNEGINTS           5
 
static PyLongObject small_ints[NSMALLNEGINTS + NSMALLPOSINTS];

次のコードを使用して、 test , 小さい整数プール内のデータが使用されているかどうかを確認します。使用されている場合、 id() の戻り値は小さい整数プール内のデータと同じです。 id 組み込み関数は、そのメモリ アドレスを返します。 Python オブジェクト。

>>> a = 1
>>> b = 2
>>> c = 1
>>> id(a), id(c)
(4343136496, 4343136496)
>>> a = -6
>>> c = -6
>>> id(a), id(c)
(4346020624, 4346021072)
>>> a = 257
>>> b = 257
>>> id(a), id(c)
(4346021104, 4346021072)
>>>

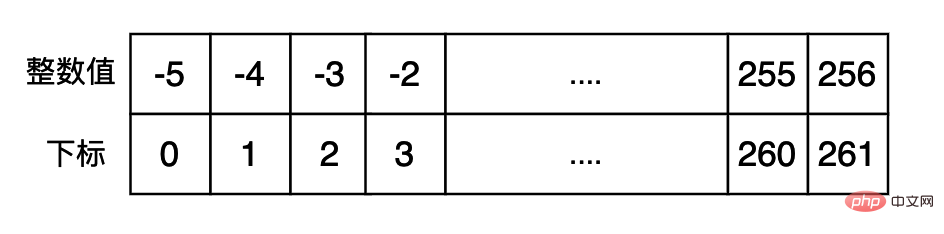上記の結果からわかることは、区間 [-5, 256] の値では、id の戻り値は実際に同じであり、戻り値はこの区間内にないということです。違います。

この機能を使用して小さなトリックを実装することもできます。これは、2 つのデータの最初のメモリ アドレス -5 と 256 を使用して、次の値を追加できるため、PyLongObject オブジェクトが占有するメモリ空間を見つけることです。このアドレスを減算すると、261 個の PyLongObject が占めるメモリ空間のサイズを取得できます (小さい整数プールには 262 個のデータがありますが、最後のデータはメモリの最後のアドレスではなく、最初のアドレスであることに注意してください)は 261 データのみ）なので、PyLongObject オブジェクトのメモリ サイズを見つけることができます。

>>> a = -5
>>> b = 256
>>> (id(b) - id(a)) / 261
32.0
>>>

上記の出力から、PyLongObject オブジェクトが 32 バイトを占有していることがわかります。次の C プログラムを使用すると、PyLongObject が占有する実際のメモリ空間を表示できます。

#include "Python.h"
#include <stdio.h>
 
int main()
{
  printf("%ld\n", sizeof(PyLongObject));
  return 0;
}

上記のプログラムの出力は次のとおりです:

上記 2 つの結果は等しいため、私たちのアイデアも検証されます。

小さい整数プールからデータを取得するためのコア コードは次のとおりです。

static PyObject *
get_small_int(sdigit ival)
{
    PyObject *v;
    assert(-NSMALLNEGINTS <= ival && ival < NSMALLPOSINTS);
    v = (PyObject *)&small_ints[ival + NSMALLNEGINTS];
    Py_INCREF(v);
    return v;
}

整数的加法实现

如果你了解过大整数加法就能够知道，大整数加法的具体实现过程了，在 cpython 内部的实现方式其实也是一样的，就是不断的进行加法操作然后进行进位操作。

#define Py_ABS(x) ((x) < 0 ? -(x) : (x)) // 返回 x 的绝对值
#define PyLong_BASE	((digit)1 << PyLong_SHIFT)
#define PyLong_MASK	((digit)(PyLong_BASE - 1))
 
 
static PyLongObject *
x_add(PyLongObject *a, PyLongObject *b)
{
    // 首先获得两个整型数据的 size 
    Py_ssize_t size_a = Py_ABS(Py_SIZE(a)), size_b = Py_ABS(Py_SIZE(b));
    PyLongObject *z;
    Py_ssize_t i;
    digit carry = 0;
    // 确保 a 保存的数据 size 是更大的
    /* Ensure a is the larger of the two: */
    if (size_a < size_b) {
        { PyLongObject *temp = a; a = b; b = temp; }
        { Py_ssize_t size_temp = size_a;
            size_a = size_b;
            size_b = size_temp; }
    }
    // 创建一个新的 PyLongObject 对象，而且数组的长度是 size_a + 1
    z = _PyLong_New(size_a+1);
    if (z == NULL)
        return NULL;
    // 下面就是整个加法操作的核心
    for (i = 0; i < size_b; ++i) {
        carry += a->ob_digit[i] + b->ob_digit[i];
        // 将低 30 位的数据保存下来
        z->ob_digit[i] = carry & PyLong_MASK;
        // 将 carry 右移 30 位，如果上面的加法有进位的话 刚好可以在下一次加法当中使用（注意上面的 carry）
        // 使用的是 += 而不是 =
        carry >>= PyLong_SHIFT; // PyLong_SHIFT = 30
    }
    // 将剩下的长度保存 （因为 a 的 size 是比 b 大的）
    for (; i < size_a; ++i) {
        carry += a->ob_digit[i];
        z->ob_digit[i] = carry & PyLong_MASK;
        carry >>= PyLong_SHIFT;
    }
    // 最后保存高位的进位
    z->ob_digit[i] = carry;
    return long_normalize(z); // long_normalize 这个函数的主要功能是保证 ob_size 保存的是真正的数据的长度 因为可以是一个正数加上一个负数 size 还变小了
}
 
PyLongObject *
_PyLong_New(Py_ssize_t size)
{
    PyLongObject *result;
    /* Number of bytes needed is: offsetof(PyLongObject, ob_digit) +
       sizeof(digit)*size.  Previous incarnations of this code used
       sizeof(PyVarObject) instead of the offsetof, but this risks being
       incorrect in the presence of padding between the PyVarObject header
       and the digits. */
    if (size > (Py_ssize_t)MAX_LONG_DIGITS) {
        PyErr_SetString(PyExc_OverflowError,
                        "too many digits in integer");
        return NULL;
    }
    // offsetof 会调用 gcc 的一个内嵌函数 __builtin_offsetof 
    // offsetof(PyLongObject, ob_digit)  这个功能是得到 PyLongObject 对象 字段 ob_digit 之前的所有字段所占的内存空间的大小
    result = PyObject_MALLOC(offsetof(PyLongObject, ob_digit) +
                             size*sizeof(digit));
    if (!result) {
        PyErr_NoMemory();
        return NULL;
    }
    // 将对象的 result 的引用计数设置成 1
    return (PyLongObject*)PyObject_INIT_VAR(result, &PyLong_Type, size);
}
 
 
static PyLongObject *
long_normalize(PyLongObject *v)
{
    Py_ssize_t j = Py_ABS(Py_SIZE(v));
    Py_ssize_t i = j;
 
    while (i > 0 && v->ob_digit[i-1] == 0)
        --i;
    if (i != j)
        Py_SIZE(v) = (Py_SIZE(v) < 0) ? -(i) : i;
    return v;
}

以上がPython 仮想マシンにおける整数の実装原理は何ですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。