カスタム クラスを使用して Java で配列をカプセル化し、データ操作を実装する方法
基本的なデータ ストレージ構造として、配列は広く使用されています。配列は、連続メモリ空間を使用して、固定長と 同じデータ型を格納するデータ構造です。データ構造は言語に依存せず、配列関連の操作には Java が使用されます。配列のインデックスは 0 から始まります。
配列の初期化
データを作成するには 2 つの方法があります。1 つは、最初に固定長データを宣言してから、配列に値を割り当てる方法です。 . もう 1 つは、 1 つ目は直接代入です。
最初の型:
数据类型[] 数组名称 = new 数据类型[长度];
ここの [] マークは配列を宣言します。この [] は、データ型の後に配置するだけでなく、データ型の後ろに配置することもできます。名詞の後でも効果は同じです。長さ 2 の型 long の配列を宣言し、値を割り当てた場合:
long[] arr = new long[2]; arr[0] = 1; arr[1] = 2;
2 番目の :
数据类型[] 数组名称 = {元素1,元素2, ...};このように、配列の初期化時に直接値が代入され、配列の長さは要素数によって決まります。
2 つのカスタム クラスは配列をカプセル化してデータ操作を実装します
public class MyArray {
// 自定义数组 private long[] arr;
// 有效数据长度 private int element;
public MyArray(){
arr = new long[9];
}
public MyArray(int maxsize){
arr = new long[maxsize];
}
/**
* 显示数组元素
*/ public void display(){
System.out.print("[");
for (int i = 0; i < element; i++) {
System.out.print(arr[i]+" ");
}
System.out.print("]");
}
}2.1 要素の追加
配列はデータを格納するために連続メモリ領域を使用するため、追加されるたびに要素を追加します現在の配列の最後の要素に追加します。要素は一度に追加できるため、複雑さは O(1) です。#9 の長さの配列を定義すると、配列にはすでに 2 つの要素があります
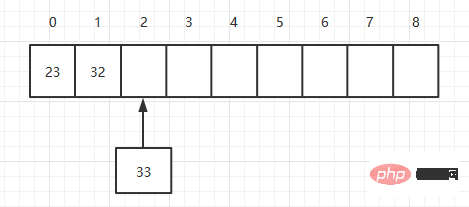
public void add(long value){
arr[element] = value;
element++;
}2.2 値に基づいて要素の位置をクエリする
この検索方法は、線形検索とも呼ばれます。値は要素をループして対応する位置を取得します。理論上、要素のクエリには平均で N/2 回かかるため、その複雑さは O(N) です。
public int find(long value){
int i;
for (i = 0; i < element; i++) {
if(value == arr[i]){
break;
}
}
if(i == element){
return -1;
}else {
return i;
}
}2.3 インデックスに従って要素をクエリする
インデックスに従って要素を検索する、つまり、対応する位置の要素を取得する場合、計算量は O(1) です。
public long get(int index){
if(index >= element || index < 0){
throw new ArrayIndexOutOfBoundsException();
}else {
return arr[index];
}
}2.4 インデックスに基づいて要素を削除する
インデックスに対応する要素を削除した後、インデックスの後のすべての要素を 1 つ前に移動する必要があります。インデックス 2 の要素を削除したい場合は、次のようにします。
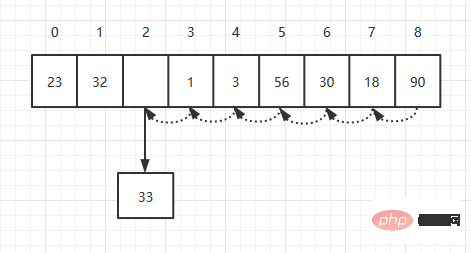
# 理論的には、要素を平均して削除するには、N/2 回移動する必要があるため、時間計算量も O(N) です。
public void delete(int index){
if(index >= element || index < 0){
throw new ArrayIndexOutOfBoundsException();
}else {
for (int i = index; i < element; i++) {
arr[index] = arr[index+1];
}
element --;
}
}2.5 要素の変更
特定の位置の要素を変更し、インデックスに従って対応する要素を直接変更するので、その時間計算量は O(1) です。
public void change(int index,long newValue){
if(index >= element || index < 0){
throw new ArrayIndexOutOfBoundsException();
}else {
arr[index] = newValue;
}
}3 順序付き配列
順序付き配列は特別なタイプの配列であり、順序付き配列内の要素は特定の順序で配置されます。
3.1 要素の追加
要素を追加する場合は、一定の位置に順番に要素を追加していきます。次のように、要素 33 を配列に追加します。
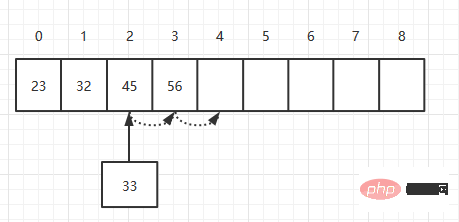
まず、インデックス 3 の要素をインデックス 4 に移動し、次にインデックス 2 の要素をインデックス 3 に移動し、最後にインデックス 2 に 33 を加算します。理論的には、要素の挿入には N/2 個の要素を移動する必要があるため、時間計算量は O(N) になります。
public void add(long value){
int i;
for (i = 0; i < element; i++) {
if(arr[i]>value){
break;
}
}
for (int j = element; j > i; j--){
arr[j] = arr[j-1];
}
arr[i] = value;
element++;
}3.2 要素に基づいてインデックスをクエリする二分法
順序なし配列で、関連する要素を見つけるには線形法を使用します。線形法とは、インデックスに従って 1 つずつ検索することです。ソートされた配列では、二分法を使用して要素を見つけることができます。二分法とは、配列を中央から 2 つに分割し、その要素がどちらの配列にあるかを判断し、この操作を繰り返すことを意味します。
8 要素を持つ配列があるとします。配列の内容は 0 ~ 7 の順序付けられたシーケンスです。要素 5 を見つけるには、要素 5 を 0 ~ 3 と 4 に分割します。初回は -7 2 つの配列、次に 4-7 を 2 つの配列 4-5 と 6-7 に分割し、最後に 4-5 を 4 と 5 に分割して特定の要素をクエリする このように、3 回分割した後、8 の配列内の特定の要素の複雑さは O(logN) の長さをクエリできます (コンピューターにおける logN の底は通常 2 を指します。これは、2 の累乗が n に等しいことを意味します)。
public int search(long value){
// 中间值 int middle = 0;
// 最小值 int low = 0;
// 最大值 int pow = element;
while (true){
middle = (low + pow) / 2;
if(arr[middle] == value){
return middle;
}else if (low > pow){
return -1;
}else{
if(arr[middle] > value){
pow = middle - 1;
}else{
low = middle + 1;
}
}
}
}4 つのまとめ
複雑さが低いほどアルゴリズムが優れていることを意味するため、O(1) > O(logN) > O(N) > O(N^2) となります。 。
| アルゴリズム | 複雑さ |
|---|---|
| 線形探索 | O (N) |
| 二分探索 | #O(logN)|
| O( 1) | |
| O(N) | |
| O( N) | |
| O(N) |
- ##順序なし配列挿入は高速ですが、検索と削除は低速です。
- 順序付けされた配列の検索は高速ですが、挿入と削除は低速です
以上がカスタム クラスを使用して Java で配列をカプセル化し、データ操作を実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7343
7343
 9
9
 1627
1627
 14
14
 1352
1352
 46
46
 1265
1265
 25
25
 1214
1214
 29
29
 Java の乱数ジェネレーター
Aug 30, 2024 pm 04:27 PM
Java の乱数ジェネレーター
Aug 30, 2024 pm 04:27 PM
Java の乱数ジェネレーターのガイド。ここでは、Java の関数について例を挙げて説明し、2 つの異なるジェネレーターについて例を挙げて説明します。
 ジャワのウェカ
Aug 30, 2024 pm 04:28 PM
ジャワのウェカ
Aug 30, 2024 pm 04:28 PM
Java の Weka へのガイド。ここでは、weka java の概要、使い方、プラットフォームの種類、利点について例を交えて説明します。
 Javaのアームストロング数
Aug 30, 2024 pm 04:26 PM
Javaのアームストロング数
Aug 30, 2024 pm 04:26 PM
Java のアームストロング番号に関するガイド。ここでは、Java でのアームストロング数の概要とコードの一部について説明します。
 Java Springのインタビューの質問
Aug 30, 2024 pm 04:29 PM
Java Springのインタビューの質問
Aug 30, 2024 pm 04:29 PM
この記事では、Java Spring の面接で最もよく聞かれる質問とその詳細な回答をまとめました。面接を突破できるように。
 Java 8 Stream Foreachから休憩または戻ってきますか?
Feb 07, 2025 pm 12:09 PM
Java 8 Stream Foreachから休憩または戻ってきますか?
Feb 07, 2025 pm 12:09 PM
Java 8は、Stream APIを導入し、データ収集を処理する強力で表現力のある方法を提供します。ただし、ストリームを使用する際の一般的な質問は次のとおりです。 従来のループにより、早期の中断やリターンが可能になりますが、StreamのForeachメソッドはこの方法を直接サポートしていません。この記事では、理由を説明し、ストリーム処理システムに早期終了を実装するための代替方法を調査します。 さらに読み取り:JavaストリームAPIの改善 ストリームを理解してください Foreachメソッドは、ストリーム内の各要素で1つの操作を実行する端末操作です。その設計意図はです







