Python で arctan 変換角度を実装する方法

デカルト座標系

平面座標系の場合、任意の光線 OP と x 軸の間の角度 θ の範囲は [0,2π) または (
デカルト空間座標系 Pc = ( x , y , z ) の点を球面座標系に表現します。 Ps = ( θ , ϕ , r ).

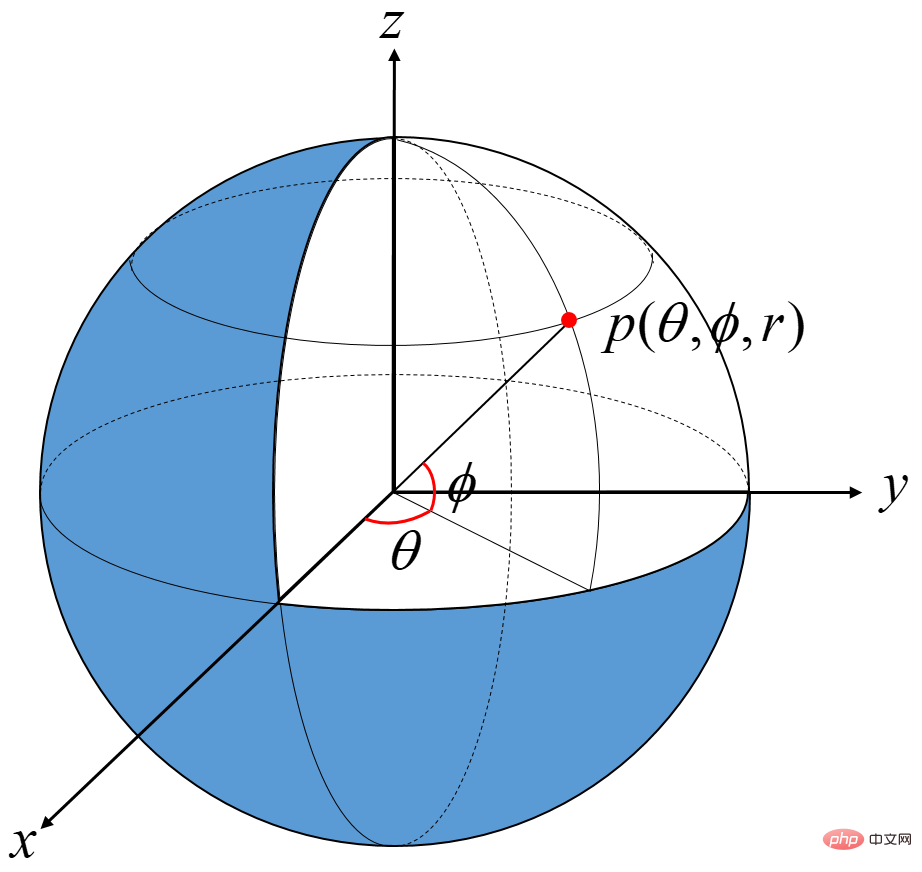
ここで

# の形式球面座標の定義によれば、θ∈[−π,π], ϕ∈[−π/2,π/2], r∈[0, ∞)。

θ の場合、正接関数の周期は π であるため、逆正接関数 arctan は通常 1 つの周期のみを取り、その定義域は R、値の範囲は (− π/2、π/2)。この問題を解決するために、arctan2 関数としても知られる Arctan 関数が導入されました。

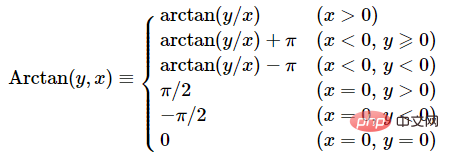
atan2 関数の使用法 atan2(delta_y, delta_x)

import math
a = math.atan2(400,-692.820)
# 2.6179936760992044
angle = a/math.pi*180
# 149.99998843242386

atan 関数の使用法 atan(delta_y / delta_x)

import math
delta_y = 400
delta_x = -692.820

if delta_x == 0:
    b = math.pi / 2.0
    angle = b/math.pi*180
    if delta_y == 0:
        angle = 0.0
    elif delta_y < 0:
        angle -= 180
else:
    b =  math.atan(delta_y/delta_x) 
    angle = b/math.pi*180
    if delta_y > 0 and delta_x < 0:
        angle = angle + 180
    if delta_y < 0 and delta_x < 0:
        angle = angle - 180

b,angle
# (-0.5235989774905888, 149.99998843242386)

atan 類似点とatan2 との違い

• パラメータの数が異なります

• #戻り値はどちらもラジアンです

• delta_x が 0 の場合でも atan2 を計算できますが、atan は事前に判定する必要があります。そうしないとプログラム エラーが発生します。

##象限処理

#atan2(b,a) は、4 象限逆正接です。その値は、正接値 b/a だけでなく、点がどの象限にあるかにも依存します ( b,a) は以下に該当します: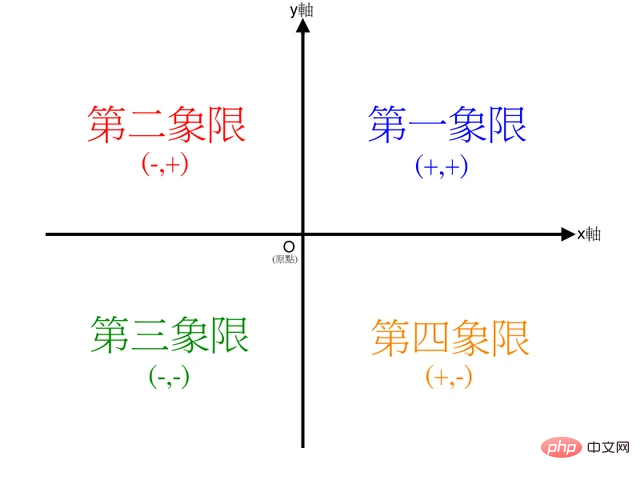

点 (b,a) が第 1 象限 (b>0、a>0) に該当する場合、atan2(b,a) の範囲は次のようになります。は

0 ~ pi /2

• ##点 (b,a) が第 2 象限 (b>0、api/2 ~ pi

• 点 (b,a) が第 3 象限 (b-pi~-pi/2

• 点 (b, a) が第 4 象限 (b0) atan2(b,a) の範囲が

  -pi/2～0

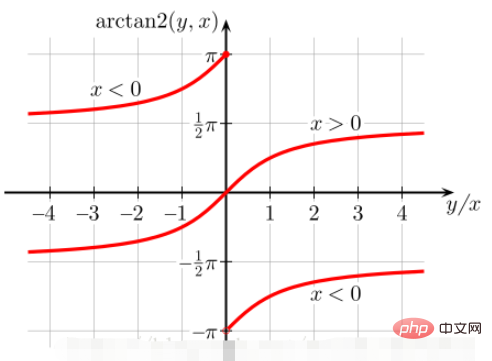
• で、atan(b/a) が a/ の場合b は正接値のみに基づいて対応する角度を見つけます (2 つの象限の逆正接とみなすことができます):

b/a > 0 の場合、値の範囲は次のようになります。 atan(b/a) は

0 ~ pi/2

• b/a -pi/2~0

• 値の範囲

Point(b ,a) 第 1 象限 (b>0, a>0)

または

第 4 象限 (b0)
• に該当する場合,

  atan2(b ,a) = atan(b/a) ##点 (b,a) は 第 2 象限 (b>0, a, b/a-pi/2~0

ですが、atan2(b,a) の範囲は) は
• pi/2 ~ pi

  であるため、atan(b/a) は角度の値を計算するために 180 を加算する必要があります。 点 (b,a) は 第 3 象限 (b, b/a>0 に該当するため、atan(b/ a) 値の範囲は

  0 ~ pi/2
で、このとき atan2(b,a) の範囲は
• -pi~-pi/2

  なので、atan(b /a ) 角度の値を計算するには、180 を引きます。 結論: atan 関数と atan2 関数。atan2 関数を使用することをお勧めします。

以上がPython で arctan 変換角度を実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。