遺伝的アルゴリズムは、ダーウィンの進化論とメンデルの遺伝学理論に基づいて、自然界の生物進化メカニズムを模倣するために開発された確率的大域探索および最適化手法です。その本質は、検索プロセス中に検索空間に関する知識を自動的に取得して蓄積し、最適なソリューションを取得するために検索プロセスを適応的に制御できる、効率的で並列的なグローバル検索方法です。遺伝的アルゴリズムの操作では、適者生存の原則を使用して、潜在的な解の集団内で最適に近い解を連続的に生成します。遺伝的アルゴリズムの各世代では、問題領域内の個人の適応度値と自然遺伝学に基づいて、中国文献から借用した再構成手法を個別の選択に使用して、新しい近似解を生成します。このプロセスは集団内の個体の進化につながり、その結果生じる新しい個体は、ちょうど自然界の変化と同じように、元の個体よりも環境によく適応します。
(1) 初期化: 進化世代カウンター t=0 を設定し、最大進化世代 T、交叉確率、突然変異確率を設定し、M をランダムに生成します。 P
(2) 個体評価：母集団内の各個体の適応度を計算 P
(3) 選択演算：母集団に選択演算子を適用します。個体の適応度に基づいて最適な個体を選択し、直接次世代に継承するか、ペア交叉により新たな個体を生成して次世代に継承する
(4) 交叉操作：交叉確率の制御下、集団 集団内の個体はペアで交配されます
(5) 突然変異操作: 突然変異確率の制御の下で、集団内の個体が突然変異します。つまり、特定の個体の遺伝子がランダムに調整されます
(6) 選択、交叉、突然変異操作を経て、次世代集団 P1 が得られます。
上記(1)～(6)を遺伝世代がTになるまで繰り返し、進化の過程で得られた最適な適応度を持つ個体を最適解出力として計算を終了します。
巡回セールスマン問題 (TSP): n 個の都市があります。セールスマンは、そのうちの 1 つの都市から出発し、すべての都市を訪問し、最初の都市に戻らなければなりません。最短ルートを見つけてください。
TSP 問題を解決するために遺伝的アルゴリズムを適用する場合、いくつかの規則を作成する必要があります。遺伝子は都市シーケンスのセットであり、適合度はこの遺伝子による都市の距離とシーケンスの 3 分の 1 です。
import random
import math
import matplotlib.pyplot as plt
# 读取数据
f=open("test.txt")
data=f.readlines()
# 将cities初始化为字典，防止下面被当成列表
cities={}
for line in data:
#原始数据以\n换行，将其替换掉
line=line.replace("\n","")
#最后一行以EOF为标志，如果读到就证明读完了，退出循环
if(line=="EOF"):
break
#空格分割城市编号和城市的坐标
city=line.split(" ")
map(int,city)
#将城市数据添加到cities中
cities[eval(city[0])]=[eval(city[1]),eval(city[2])]
# 计算适应度，也就是距离分之一，这里用伪欧氏距离
def calcfit(gene):
sum=0
#最后要回到初始城市所以从-1，也就是最后一个城市绕一圈到最后一个城市
for i in range(-1,len(gene)-1):
nowcity=gene[i]
nextcity=gene[i+1]
nowloc=cities[nowcity]
nextloc=cities[nextcity]
sum+=math.sqrt(((nowloc[0]-nextloc[0])**2+(nowloc[1]-nextloc[1])**2)/10)
return 1/sum
# 每个个体的类，方便根据基因计算适应度
class Person:
def __init__(self,gene):
self.gene=gene
self.fit=calcfit(gene)
class Group:
def __init__(self):
self.GroupSize=100 #种群规模
self.GeneSize=48 #基因数量，也就是城市数量
self.initGroup()
self.upDate()
#初始化种群，随机生成若干个体
def initGroup(self):
self.group=[]
i=0
while(i<self.GroupSize):
i+=1
#gene如果在for以外生成只会shuffle一次
gene=[i+1 for i in range(self.GeneSize)]
random.shuffle(gene)
tmpPerson=Person(gene)
self.group.append(tmpPerson)
#获取种群中适应度最高的个体
def getBest(self):
bestFit=self.group[0].fit
best=self.group[0]
for person in self.group:
if(person.fit>bestFit):
bestFit=person.fit
best=person
return best
#计算种群中所有个体的平均距离
def getAvg(self):
sum=0
for p in self.group:
sum+=1/p.fit
return sum/len(self.group)
#根据适应度，使用轮盘赌返回一个个体，用于遗传交叉
def getOne(self):
#section的简称，区间
sec=[0]
sumsec=0
for person in self.group:
sumsec+=person.fit
sec.append(sumsec)
p=random.random()*sumsec
for i in range(len(sec)):
if(p>sec[i] and p<sec[i+1]):
#这里注意区间是比个体多一个0的
return self.group[i]
#更新种群相关信息
def upDate(self):
self.best=self.getBest()
# 遗传算法的类，定义了遗传、交叉、变异等操作
class GA:
def __init__(self):
self.group=Group()
self.pCross=0.35 #交叉率
self.pChange=0.1 #变异率
self.Gen=1 #代数
#变异操作
def change(self,gene):
#把列表随机的一段取出然后再随机插入某个位置
#length是取出基因的长度，postake是取出的位置，posins是插入的位置
geneLenght=len(gene)
index1 = random.randint(0, geneLenght - 1)
index2 = random.randint(0, geneLenght - 1)
newGene = gene[:] # 产生一个新的基因序列，以免变异的时候影响父种群
newGene[index1], newGene[index2] = newGene[index2], newGene[index1]
return newGene
#交叉操作
def cross(self,p1,p2):
geneLenght=len(p1.gene)
index1 = random.randint(0, geneLenght - 1)
index2 = random.randint(index1, geneLenght - 1)
tempGene = p2.gene[index1:index2] # 交叉的基因片段
newGene = []
p1len = 0
for g in p1.gene:
if p1len == index1:
newGene.extend(tempGene) # 插入基因片段
p1len += 1
if g not in tempGene:
newGene.append(g)
p1len += 1
return newGene
#获取下一代
def nextGen(self):
self.Gen+=1
#nextGen代表下一代的所有基因
nextGen=[]
#将最优秀的基因直接传递给下一代
nextGen.append(self.group.getBest().gene[:])
while(len(nextGen)<self.group.GroupSize):
pChange=random.random()
pCross=random.random()
p1=self.group.getOne()
if(pCross<self.pCross):
p2=self.group.getOne()
newGene=self.cross(p1,p2)
else:
newGene=p1.gene[:]
if(pChange<self.pChange):
newGene=self.change(newGene)
nextGen.append(newGene)
self.group.group=[]
for gene in nextGen:
self.group.group.append(Person(gene))
self.group.upDate()
#打印当前种群的最优个体信息
def showBest(self):
print("第{}代\t当前最优{}\t当前平均{}\t".format(self.Gen,1/self.group.getBest().fit,self.group.getAvg()))
#n代表代数，遗传算法的入口
def run(self,n):
Gen=[] #代数
dist=[] #每一代的最优距离
avgDist=[] #每一代的平均距离
#上面三个列表是为了画图
i=1
while(i<n):
self.nextGen()
self.showBest()
i+=1
Gen.append(i)
dist.append(1/self.group.getBest().fit)
avgDist.append(self.group.getAvg())
#绘制进化曲线
plt.plot(Gen,dist,'-r')
plt.plot(Gen,avgDist,'-b')
plt.show()
ga=GA()
ga.run(3000)
print("进行3000代后最优解：",1/ga.group.getBest().fit)下の図は実験結果のスクリーンショットです。最適解は 11271
# です。 
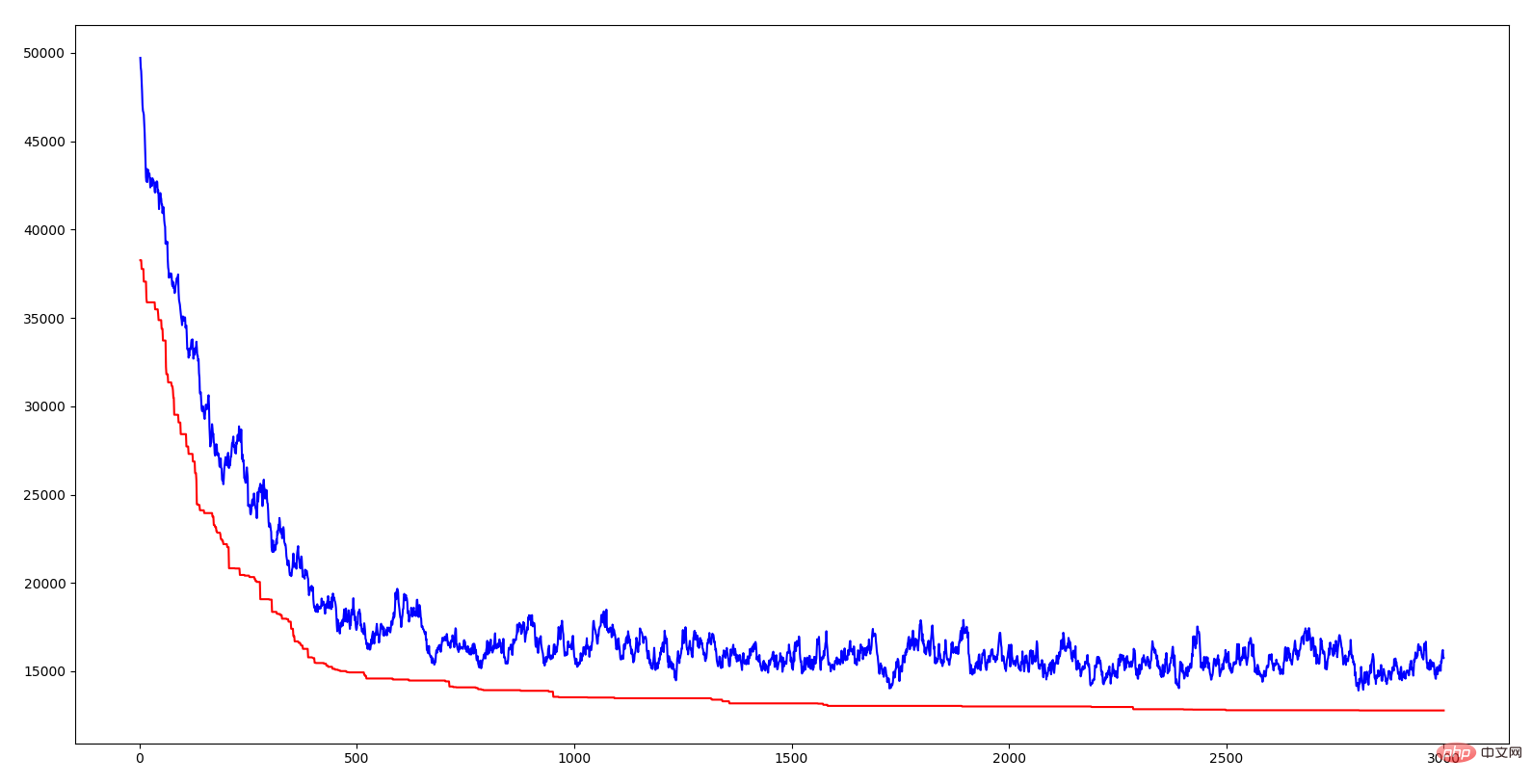#上図の横軸は代数、縦軸は距離、赤い曲線は最適個体の距離です。曲線は各世代の平均距離です。どちらの線も下降傾向にあり、進化していることがわかります。平均距離の減少は、優れた遺伝子 (つまり、特定の都市配列) の出現により、この優れた形質が急速に人口全体に広がることを示しています。自然界の適者生存と同じように、環境に適応した遺伝子を持ったものだけが生き残ることができ、それに応じて生き残るのは、優れた遺伝子を持ったものです。アルゴリズムに交叉率と突然変異率を導入する意義は、現在の優れた遺伝子を確保し、より良い遺伝子を生成しようとすることです。すべての個体が交叉すると、いくつかの優れた遺伝子セグメントが失われる可能性があり、いずれも交叉しない場合、2 つの優れた遺伝子セグメントを組み合わせてより良い遺伝子を作ることはできず、変異がなければ、より環境に適応した個体を生み出すことはできません。自然の知恵はとても強力だとため息をつきます。
上記の遺伝子フラグメントは TSP の短い都市シーケンスであり、あるシーケンスの距離の合計が比較的小さい場合、このシーケンスはこれらの都市の横断順序が比較的良好であることを意味します。遺伝的アルゴリズムは、これらの優れたフラグメントを組み合わせることにより、TSP ソリューションの継続的な最適化を実現します。この組み合わせ方法は、自然の知恵、継承、突然変異、適者生存を利用しています。
1.4 実験の概要
具体的な実装過程でミスをしてしまいましたが、当初、遺伝ステップで個体を選別する際に、個体を選択するたびにその個体を集団から削除してしまいました。今考えると非常に愚かなやり方で、当時すでにルーレットを実装していましたが、個体を選択して削除すると各個体が平等に子孫を産むことになります。適応度の高いものから優先的に継承させます。このアプローチは、「適者生存」という本来の意図から完全に逸脱しています。遺伝する個体を選択して集団に戻すのが正しいアプローチであり、これにより適応度の高い個体が複数回受け継がれ、より多くの子孫を残し、優れた遺伝子をより広く広めることができる。子孫をほとんど残さないか、直接淘汰されてしまいます。
いわゆる前進とは、次の世代の最適な個体が前世代よりも環境に同等以上に適応できる必要があることを意味します。私が採用している方法は、交叉突然変異などの操作に参加せずに、最適な個体が直接次世代に入るというものです。これにより、これらの操作により現在最良の遺伝子が逆進化によって「汚染」されるのを防ぐことができます。
また、実装プロセス中に、参照渡しまたは値渡しが原因であった別の問題にも遭遇しました。個々の遺伝子の交叉や突然変異にはリストが使用されますが、Python でこのリストを渡す場合、実際にはリストが参照されるため、交叉や突然変異後にその個体自身の遺伝子が変更されてしまいます。その結果、逆進化を伴う非常に遅い進化が起こります。
ある個体の断片を選択して別の個体に入れ、重複していない遺伝子を順番に他の位置に入れます。
このステップを実装する際、私は生物学を勉強するときの実際の染色体の動作、「相同染色体は相同セグメントを交差して交換する」という本質的な理解を持っていたため、この関数を誤って実装してしまいました。同じ位置にある 2 人の人物の断片を交換するだけでクロスオーバーを完成させましたが、明らかにこのアプローチは間違っており、都市の重複につながります。
その後のテストで、パラメータの変更や個別情報の更新が面倒だったので、すべてをOOPに変更したのが非常に便利でした。 OOP は、このような現実世界の問題をシミュレートするための優れた柔軟性とシンプルさを提供します。
テストの過程で、局所的な最適解が時折現れ、それは長期間進化し続けず、現時点での解は最適解から遠く離れていることが判明しました。その後の調整を経ても、最適解に近づいてはいるものの、まだ最適解には到達していないため、「局所最適」であることに変わりはありません。
アルゴリズムは最初はすぐに収束しますが、進行するにつれて徐々に遅くなるか、まったく動かなくなることもあります。後期段階ではすべての個体が比較的類似した優れた遺伝子を持っているため、この時点での進化に対する交叉の影響は非常に弱く、進化の主な原動力は突然変異となり、突然変異は暴力的なアルゴリズムである。運が良ければ、より良い個体にすぐに変異することができますが、運が悪い場合は待たなければなりません。
局所最適解を防ぐ解決策は、個体の突然変異がより多くなり、進化した個体が生み出される可能性が高くなるように、集団のサイズを大きくすることです。母集団サイズを増やすことの欠点は、各世代の計算時間が長くなることであり、これは 2 つが互いに阻害し合うことを意味します。母集団サイズが巨大であれば、最終的には局所最適解を回避できるが、各世代に時間がかかり、最適解を見つけるまでに長い時間がかかる一方、母集団サイズが小さいと、各世代の計算時間は速いが、最適解を見つけることはできない。数世代後に解決され、局所最適に陥ります。
考えられる最適化手法としては、進化の初期段階では集団サイズを小さくして進化を加速し、適応度が一定の閾値に達したら、極大値を避けるために集団サイズと突然変異率を大きくするという方法が考えられます。優れたソリューションの出現。この動的調整方法は、各世代の計算効率と全体の計算効率の間のバランスを比較検討するために使用されます。
以上がPython を使用して遺伝的アルゴリズムを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
![[Web フロントエンド] Node.js クイック スタート](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
