Java のバイナリ ツリーの基本的な知識と概念は何ですか?
1. ツリー構造
1.1 概念
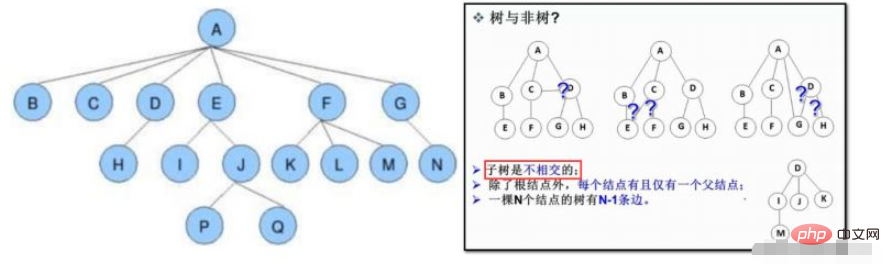
ツリーは、n (n> ; n) で構成される非線形データ構造です。 =0) 有限ノードは階層関係を持つセットを形成します。逆さまの木、つまり根が上を向き、葉が下を向いているように見えるので、木と呼ばれます。
1.2 概念 (重要)
a. ノードの次数: ノードのサブツリーの数; 上に示すように: A の次数は 6, J の次数は 2
b です。ツリーの次数: このツリーでは、上の図に示すように、最大のノードの次数が数値の次数になります。ツリーは 6
c. リーフ ノード (ターミナル ノード): 次数 0 のノード (サブツリーのないノード)
d. 親ノード/親ノード: 上に示すように: D は H
の親ノードです。子ノード/子ノード: 上の図に示すように: H は D
e の子ノードです。ルート ノード: 親のないノード。上の図に示されている: A
f. ノード レベル: ルートから開始して、ルートはレベル 1、ルートの子ノードはレベル 2、などとなります;
g.ツリーの高さまたは深さ: ツリー内のノードの最大レベル; 上に示すように: ツリーの高さは 4
2. バイナリ ツリー (キー ポイント)
2.1 概念
各ノードには、次数
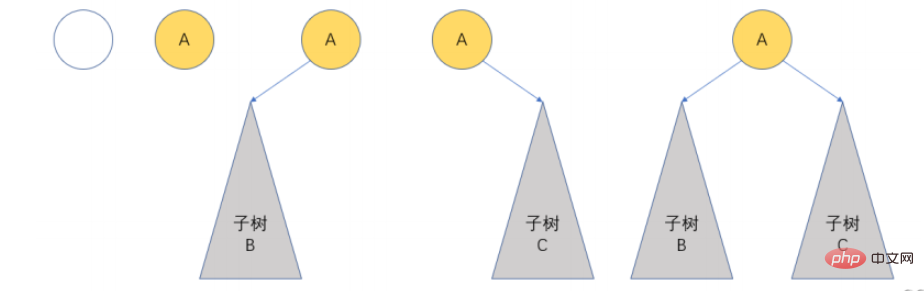
2.2 バイナリ ツリーの基本形式
##2.3 2 つの特別なバイナリ木
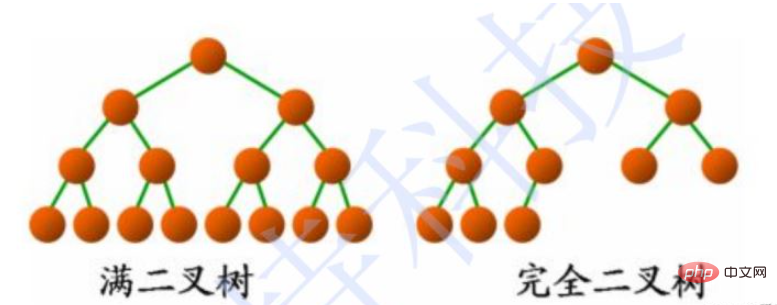
a. 完全な二分木: 非子葉次数は 2
b. 完全な二分木: 完全な二分木には「右下」がありません。
2.4 バイナリ ツリーのプロパティ
a. 完全なバイナリ ツリー
1. 高さは K なので、2^k-1 個あります。ノード
2。レベルが K の場合、レイヤーには 2^(k-1) ノード
3があります。エッジの数 = ノード数 - 1
4。次数 0 の n0 と次数 2 の n2 があり、n0 = n2 1
b. 完全な二分木
1. 正しい子があれば、左の子が存在する必要があります
2。次数 1 のノードは 1 つだけ存在できます
2.5 バイナリ ツリーのストレージ
バイナリ ツリーのストレージ構造は、次のように分割されます。 : 順次ストレージとリンクされたリストのようなストレージ。
シーケンシャル ストレージ: 完全なバイナリ ツリーのみを保存できます
チェーン ストレージ: 通常のバイナリ ツリー
今回はチェーン ストレージを紹介します
二分木はノードによって 1 つずつ参照されます。一般的な表現方法には二分表現と三分岐表現が含まれます。
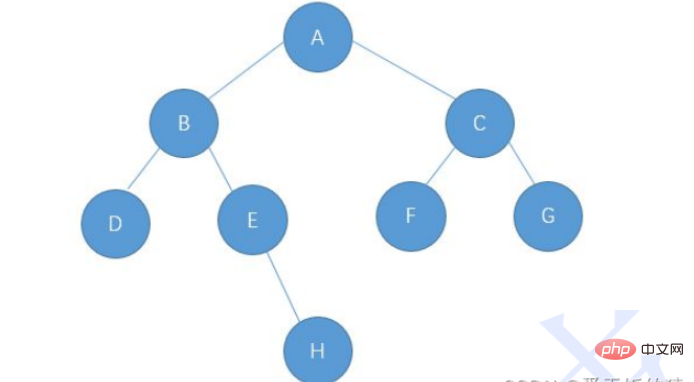
この図を例として取り上げます。詳細は次のとおりです。
// 孩子表示法
private static class TreeNode{
char val;
TreeNode left;
TreeNode right;
public TreeNode(char val) {
this.val = val;
}
}初期化:
public static TreeNode build(){
TreeNode nodeA=new TreeNode('A');
TreeNode nodeB=new TreeNode('B');
TreeNode nodeC=new TreeNode('C');
TreeNode nodeD=new TreeNode('D');
TreeNode nodeE=new TreeNode('E');
TreeNode nodeF=new TreeNode('F');
TreeNode nodeG=new TreeNode('G');
TreeNode nodeH=new TreeNode('H');
nodeA.left=nodeB;
nodeA.right=nodeC;
nodeB.left=nodeD;
nodeB.right=nodeE;
nodeE.right=nodeH;
nodeC.left=nodeF;
nodeC.right=nodeG;
return nodeA;
}2.6 バイナリ ツリーの基本操作
2.6.1 バイナリ ツリー トラバーサル (再帰)
1. NLR: プリオーダー トラバーサル (別名: Preorder Traversal) Preorder Traversal) Order Traversal)—— ルート ノードにアクセスします ---> ルートの左側のサブツリー ---> ルートの右側のサブツリーにアクセスします。
//先序遍历 : 根左右
public static void preOrder(TreeNode root){
if(root==null){
return;
}
System.out.print(root.val+" ");
preOrder(root.left);
preOrder(root.right);
}2. LNR: Inorder Traversal (Inorder Traversal)—— ルートの左側のサブツリー ---> ルート ノード ---> ルートの右側のサブツリー。
//中序遍历
public static void inOrder(TreeNode root){
if(root==null){
return;
}
preOrder(root.left);
System.out.print(root.val+" ");
preOrder(root.right);
}3. LRN: ポストオーダー トラバーサル - ルートの左サブツリー ---> ルートの右サブツリー ---> ルート ノード。
//后序遍历
public static void postOrder(TreeNode root){
if(root==null){
return;
}
preOrder(root.left);
preOrder(root.right);
System.out.print(root.val+" ");
}2.6.2 バイナリ ツリー トラバーサル (反復)
1. プレオーダー トラバーサル
//方法2(迭代)
//先序遍历 (迭代)
public static void preOrderNonRecursion(TreeNode root){
if(root==null){
return ;
}
Deque<TreeNode> stack=new LinkedList<>();
stack.push(root);
while (!stack.isEmpty()){
TreeNode cur=stack.pop();
System.out.print(cur.val+" ");
if(cur.right!=null){
stack.push(cur.right);
}
if(cur.left!=null){
stack.push(cur.left);
}
}
}2. インオーダー トラバーサル
//方法2(迭代)
//中序遍历 (迭代)
public static void inorderTraversalNonRecursion(TreeNode root) {
if(root==null){
return ;
}
Deque<TreeNode> stack=new LinkedList<>();
// 当前走到的节点
TreeNode cur=root;
while (!stack.isEmpty() || cur!=null){
// 不管三七二十一,先一路向左走到根儿~
while (cur!=null){
stack.push(cur);
cur=cur.left;
}
// 此时cur为空,说明走到了null,此时栈顶就存放了左树为空的节点
cur=stack.pop();
System.out.print(cur.val+" ");
// 继续访问右子树
cur=cur.right;
}
}3. ポストオーダー トラバーサル トラバース
//方法2(迭代)
//后序遍历 (迭代)
public static void postOrderNonRecursion(TreeNode root){
if(root==null){
return;
}
Deque<TreeNode> stack=new LinkedList<>();
TreeNode cur=root;
TreeNode prev=null;
while (!stack.isEmpty() || cur!=null){
while (cur!=null){
stack.push(cur);
cur=cur.left;
}
cur=stack.pop();
if(cur.right==null || prev==cur.right){
System.out.print(cur.val+" ");
prev=cur;
cur=null;
}else {
stack.push(cur);
cur=cur.right;
}
}
}2.6.3 バイナリ ツリーの基本操作
1. ノード数を求める (再帰と反復)
//方法1(递归)
//传入一颗二叉树的根节点,就能统计出当前二叉树中一共有多少个节点,返回节点数
//此时的访问就不再是输出节点值,而是计数器 + 1操作
public static int getNodes(TreeNode root){
if(root==null){
return 0;
}
return 1+getNodes(root.left)+getNodes(root.right);
}
//方法2(迭代)
//使用层序遍历来统计当前树中的节点个数
public static int getNodesNoRecursion(TreeNode root){
if(root==null){
return 0;
}
int size=0;
Deque<TreeNode> queue=new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
size++;
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
return size;
}2. 葉ノードの数を求める (再帰と反復) iteration)
//方法1(递归)
//传入一颗二叉树的根节点,就能统计出当前二叉树的叶子结点个数
public static int getLeafNodes(TreeNode root){
if(root==null){
return 0;
}
if(root.left==null && root.right==null){
return 1;
}
return getLeafNodes(root.left)+getLeafNodes(root.right);
}
//方法2(迭代)
//使用层序遍历来统计叶子结点的个数
public static int getLeafNodesNoRecursion(TreeNode root){
if(root==null){
return 0;
}
int size=0;
Deque<TreeNode> queue=new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()){
TreeNode cur=queue.poll();
if(cur.left==null && cur.right==null){
size++;
}
if(cur.left!=null){
queue.offer(cur.left);
}
if(cur.right!=null){
queue.offer(cur.right);
}
}
return size;
}3. k 番目の層のノード数を求める
//求出以root为根节点的二叉树第k层的节点个数
public static int getKLevelNodes(TreeNode root,int k){
if(root==null || k<=0){
return 0;
}
if(k==1){
return 1;
}
return getKLevelNodes(root.left,k-1)+getKLevelNodes(root.right,k-1);
}4. 木の高さを求める
//传入一个以root为根节点的二叉树,就能求出该树的高度
public static int height(TreeNode root){
if(root==null){
return 0;
}
return 1+ Math.max(height(root.left),height(root.right));
}5. 値があるかどうかを判定する値のノード
//判断当前以root为根节点的二叉树中是否包含指定元素val,
//若存在返回true,不存在返回false
public static boolean contains(TreeNode root,char value){
if(root==null){
return false;
}
if(root.val==value){
return true;
}
return contains(root.left,value) || contains(root.right,value);
}2.7 二分木のレベル順走査
//层序遍历
public static void levelOrder(TreeNode root) {
if(root==null){
return ;
}
// 借助队列来实现遍历过程
Deque<TreeNode> queue =new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()){
int size=queue.size();
for (int i = 0; i < size; i++) {
TreeNode cur=queue.poll();
System.out.print(cur.val+" ");
if(cur.left!=null){
queue.offer(cur.left);
}
if(cur.right!=null){
queue.offer(cur.right);
}
}
}
}以上がJava のバイナリ ツリーの基本的な知識と概念は何ですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 1662
1662
 14
14
 1419
1419
 52
52
 1313
1313
 25
25
 1262
1262
 29
29
 1235
1235
 24
24
 Java 8 Stream Foreachから休憩または戻ってきますか?
Feb 07, 2025 pm 12:09 PM
Java 8 Stream Foreachから休憩または戻ってきますか?
Feb 07, 2025 pm 12:09 PM
Java 8は、Stream APIを導入し、データ収集を処理する強力で表現力のある方法を提供します。ただし、ストリームを使用する際の一般的な質問は次のとおりです。 従来のループにより、早期の中断やリターンが可能になりますが、StreamのForeachメソッドはこの方法を直接サポートしていません。この記事では、理由を説明し、ストリーム処理システムに早期終了を実装するための代替方法を調査します。 さらに読み取り:JavaストリームAPIの改善 ストリームを理解してください Foreachメソッドは、ストリーム内の各要素で1つの操作を実行する端末操作です。その設計意図はです
 PHP:Web開発の重要な言語
Apr 13, 2025 am 12:08 AM
PHP:Web開発の重要な言語
Apr 13, 2025 am 12:08 AM
PHPは、サーバー側で広く使用されているスクリプト言語で、特にWeb開発に適しています。 1.PHPは、HTMLを埋め込み、HTTP要求と応答を処理し、さまざまなデータベースをサポートできます。 2.PHPは、ダイナミックWebコンテンツ、プロセスフォームデータ、アクセスデータベースなどを生成するために使用され、強力なコミュニティサポートとオープンソースリソースを備えています。 3。PHPは解釈された言語であり、実行プロセスには語彙分析、文法分析、編集、実行が含まれます。 4.PHPは、ユーザー登録システムなどの高度なアプリケーションについてMySQLと組み合わせることができます。 5。PHPをデバッグするときは、error_reporting()やvar_dump()などの関数を使用できます。 6. PHPコードを最適化して、キャッシュメカニズムを使用し、データベースクエリを最適化し、組み込み関数を使用します。 7
 PHP対Python:違いを理解します
Apr 11, 2025 am 12:15 AM
PHP対Python:違いを理解します
Apr 11, 2025 am 12:15 AM
PHP and Python each have their own advantages, and the choice should be based on project requirements. 1.PHPは、シンプルな構文と高い実行効率を備えたWeb開発に適しています。 2。Pythonは、簡潔な構文とリッチライブラリを備えたデータサイエンスと機械学習に適しています。
 PHP対その他の言語:比較
Apr 13, 2025 am 12:19 AM
PHP対その他の言語:比較
Apr 13, 2025 am 12:19 AM
PHPは、特に迅速な開発や動的なコンテンツの処理に適していますが、データサイエンスとエンタープライズレベルのアプリケーションには良くありません。 Pythonと比較して、PHPはWeb開発においてより多くの利点がありますが、データサイエンスの分野ではPythonほど良くありません。 Javaと比較して、PHPはエンタープライズレベルのアプリケーションでより悪化しますが、Web開発により柔軟性があります。 JavaScriptと比較して、PHPはバックエンド開発により簡潔ですが、フロントエンド開発のJavaScriptほど良くありません。
 PHP対Python:コア機能と機能
Apr 13, 2025 am 12:16 AM
PHP対Python:コア機能と機能
Apr 13, 2025 am 12:16 AM
PHPとPythonにはそれぞれ独自の利点があり、さまざまなシナリオに適しています。 1.PHPはWeb開発に適しており、組み込みのWebサーバーとRich Functionライブラリを提供します。 2。Pythonは、簡潔な構文と強力な標準ライブラリを備えたデータサイエンスと機械学習に適しています。選択するときは、プロジェクトの要件に基づいて決定する必要があります。
 カプセルの量を見つけるためのJavaプログラム
Feb 07, 2025 am 11:37 AM
カプセルの量を見つけるためのJavaプログラム
Feb 07, 2025 am 11:37 AM
カプセルは3次元の幾何学的図形で、両端にシリンダーと半球で構成されています。カプセルの体積は、シリンダーの体積と両端に半球の体積を追加することで計算できます。このチュートリアルでは、さまざまな方法を使用して、Javaの特定のカプセルの体積を計算する方法について説明します。 カプセルボリュームフォーミュラ カプセルボリュームの式は次のとおりです。 カプセル体積=円筒形の体積2つの半球体積 で、 R:半球の半径。 H:シリンダーの高さ(半球を除く)。 例1 入力 RADIUS = 5ユニット 高さ= 10単位 出力 ボリューム= 1570.8立方ユニット 説明する 式を使用してボリュームを計算します。 ボリューム=π×R2×H(4
 PHPの影響:Web開発など
Apr 18, 2025 am 12:10 AM
PHPの影響:Web開発など
Apr 18, 2025 am 12:10 AM
phphassiblasifly-impactedwebdevevermentandsbeyondit.1)itpowersmajorplatformslikewordpratsandexcelsindatabase interactions.2)php'sadaptableability allowsitale forlargeapplicationsusingframeworkslikelavel.3)
 PHP対Python:ユースケースとアプリケーション
Apr 17, 2025 am 12:23 AM
PHP対Python:ユースケースとアプリケーション
Apr 17, 2025 am 12:23 AM
PHPはWeb開発およびコンテンツ管理システムに適しており、Pythonはデータサイエンス、機械学習、自動化スクリプトに適しています。 1.PHPは、高速でスケーラブルなWebサイトとアプリケーションの構築においてうまく機能し、WordPressなどのCMSで一般的に使用されます。 2。Pythonは、NumpyやTensorflowなどの豊富なライブラリを使用して、データサイエンスと機械学習の分野で驚くほどパフォーマンスを発揮しています。




