Java での Timsort ソート アルゴリズムの手順と実装

背景

Timsort は、ハイブリッドで安定した並べ替えアルゴリズムです。簡単に言うと、merge sort アルゴリズムと binary insert sort アルゴリズムを組み合わせたものです。世界最高のソート アルゴリズムとして 最高のソート アルゴリズム。 Timsort は常に Python の標準ソート アルゴリズムです。 Timsort API は Java SE 7 以降に追加されました。 Arrays.sort から、これがすでに 非プリミティブ型配列 のデフォルトのソート アルゴリズムであることがわかります。したがって、高度なプログラミング学習であっても、面接であっても、Timsort を理解することがより重要です。

// List sort()    
default void sort(Comparator<? super E> c) {
        Object[] a = this.toArray();
              //数组排序
        Arrays.sort(a, (Comparator) c);
              ...
    }

// Arrays.sort
    public static <T> void sort(T[] a, Comparator<? super T> c) {
        if (c == null) {
            sort(a);
        } else {
              // 废弃版本
            if (LegacyMergeSort.userRequested)
                legacyMergeSort(a, c);
            else
                TimSort.sort(a, 0, a.length, c, null, 0, 0);
        }
    }

    public static void sort(Object[] a) {
        if (LegacyMergeSort.userRequested)
            legacyMergeSort(a);
        else
            ComparableTimSort.sort(a, 0, a.length, null, 0, 0);
    }

前提知識

Timsort を理解するには、まず次の知識を確認する必要があります。

指数関数的検索

指数関数的検索は二重検索とも呼ばれ、大きな配列内の要素を検索するために作成されたアルゴリズムです。これは 2 段階のプロセスです。まず、アルゴリズムはターゲット要素が存在する範囲 (L,R) を見つけようとし、次にこの範囲内で二分探索を使用してターゲットの正確な位置を見つけます。時間計算量は O(lgn) です。この検索アルゴリズムは、大規模な順序配列で効果的です。

バイナリ挿入ソート

挿入ソート アルゴリズムは非常に単純で、一般的なプロセスは 2 番目の要素から開始して前方に進み、適切な位置が見つかるまで要素を交換します。

挿入ソートの最適な時間計算量も O(n) です。二分探索を使用すると、挿入中の要素の比較の数を減らし、時間計算量をログインしました。ただし、二分探索挿入ソートでも同じ数の要素を移動する必要がありますが、配列のコピーにかかる時間は 1 つずつのスワップ操作よりも短いことに注意してください。

機能: バイナリ挿入ソートの主な利点は、小さいデータ セットのシナリオでソート効率が非常に高いことです。

public static int[] sort(int[] arr) throws Exception {
        // 开始遍历第一个元素后的所有元素
        for (int i = 1; i < arr.length; i++) {
            // 需要插入的元素
            int tmp = arr[i];
            // 从已排序最后一个元素开始，如果当前元素比插入元素大，就往后移动
            int j = i;
            while (j > 0 && tmp < arr[j - 1]) {
                arr[j] = arr[j - 1];
                j--;
            }
            // 将元素插入
            if (j != i) {
                arr[j] = tmp;
            }
        }
        return arr;
    }

    public static int[] binarySort(int[] arr) throws Exception {
        for (int i = 1; i < arr.length; i++) {
            // 需要插入的元素
            int tmp = arr[i];
            // 通过二分查找直接找到插入位置
            int j = Math.abs(Arrays.binarySearch(arr, 0, i, tmp) + 1);
            // 找到插入位置后，通过数组复制向后移动，腾出元素位置
            System.arraycopy(arr, j, arr, j + 1, i - j);
            // 将元素插入
            arr[j] = tmp;
        }
        return arr;
    }

マージ ソート

マージ ソートは分割統治戦略を利用するアルゴリズムであり、2 つの主要な操作 (Split と Merge) が含まれています。 。一般的なプロセスは、分割できなくなるまで配列を 2 つの半分に再帰的に分割し (つまり、配列が空になるか、要素が 1 つだけ残っている状態)、その後マージして並べ替えます。簡単に言えば、マージ操作は、ソートされた 2 つの小さな配列を継続的に取得し、それらを結合して大きな配列を作成することです。

機能: マージ ソートは、主に大規模なデータ セットのシナリオ向けに設計された並べ替えアルゴリズムです。

public static void mergeSortRecursive(int[] arr, int[] result, int start, int end) {
        // 跳出递归
        if (start >= end) {
            return;
        }
        // 待分割的数组长度
        int len = end - start;
        int mid = (len >> 1) + start;
        int left = start; // 左子数组开始索引
        int right = mid + 1; // 右子数组开始索引
        // 递归切割左子数组，直到只有一个元素
        mergeSortRecursive(arr, result, left, mid);
        // 递归切割右子数组，直到只有一个元素
        mergeSortRecursive(arr, result, right, end);
        int k = start;
        while (left <= mid && right <= end) {
            result[k++] = arr[left] < arr[right] ? arr[left++] : arr[right++];
        }
        while (left <= mid) {
            result[k++] = arr[left++];
        }
        while (right <= end) {
            result[k++] = arr[right++];
        }
        for (k = start; k <= end; k++) {
            arr[k] = result[k];
        }
    }

    public static int[] merge_sort(int[] arr) {
        int len = arr.length;
        int[] result = new int[len];
        mergeSortRecursive(arr, result, 0, len - 1);
        return arr;
    }

Timsort 実行プロセス

配列の長さが指定されたしきい値 (MIN_MERGE) より小さい場合のアルゴリズムの一般的なプロセス)、直接使用します。バイナリ挿入アルゴリズムによって並べ替えが完了します。そうでない場合は、次の手順を実行します。

• 配列の左側から開始して、Ascending order# を実行します。 ## を使用して subsequence を取得します。

• この

  サブシーケンス を実行スタックに置き、 がマージ を実行するまで待ちます。

• 実行スタック内の

  サブシーケンス を確認し、マージ条件が満たされている場合はマージを実行します。

• 最初のステップを繰り返し、次の

  昇順実行を実行します。

昇順演算

昇順演算は、連続的な増加 (昇順) または減少 (降順) の部分列をサブシーケンスの場合、シーケンスが降順の場合は、それを昇順に反転します。このプロセスは、run とも呼ばれます。たとえば、配列 [2,3,6,4,9,30] では、[2,3,6]、[4,9]、[30]、または 3 run の 3 つのサブシーケンスを見つけることができます。 ＃＃＃。 いくつかのキーのしきい値

MIN_MERGE

これは定数値であり、単純にマージの最小しきい値として理解できます。 length それより小さい場合は、このような複雑なソートを行う必要はなく、バイナリ挿入だけで済みます。 Tim Peter の C 実装では 64 ですが、実際の経験では 32 に設定した方がうまく機能するため、Java の値は 32 です。

降順を反転する際の安定性を確保するために、同じ要素は反転されません。

minrun

シーケンスをマージするとき、数値

run

が 2 の累乗以下の場合、マージします。最も効率が高く、2 のべき乗よりわずかに大きい場合、効率は大幅に低下します。したがって、マージの効率を向上させるためには、各 run の長さを可能な限り制御する必要があります。 ##run、長さが短すぎる場合は、バイナリ挿入ソートを使用して、run の後の要素を前の run に挿入します。 通常、ソート アルゴリズムを実行する前に、この minrun が最初に計算されます (データの特性に応じて自動的に調整されます)。minrun は 32 ～ 64 の数値を選択するため、データのサイズは分割されますby minrun は 2 の累乗に等しいか、わずかに小さいです。たとえば、長さが 65 の場合、minrun の値は 33 になり、長さが 165 の場合、minrun の値は 42 になります。

看下 Java 里面的实现，如果数据长度（n） < MIN_MERGE，则返回数据长度。如果数据长度恰好是 2 的幂次方，则返回MIN_MERGE/2
也就是16，否则返回一个MIN_MERGE/2 <= k <= MIN_MERGE范围的值k，这样可以使的 n/k 接近但严格小于 2 的幂次方。

private static int minRunLength(int n) {
        assert n >= 0;
        int r = 0;      // 如果低位任何一位是1，就会变成1
        while (n >= MIN_MERGE) {
            r |= (n & 1);
            n >>= 1;
        }
        return n + r;
    }

MIN_GALLOP

MIN_GALLOP 是为了优化合并的过程设定的一个阈值，控制进入 GALLOP 模式中， GALLOP 模式放在后面讲。

下面是 Timsort 执行流程图

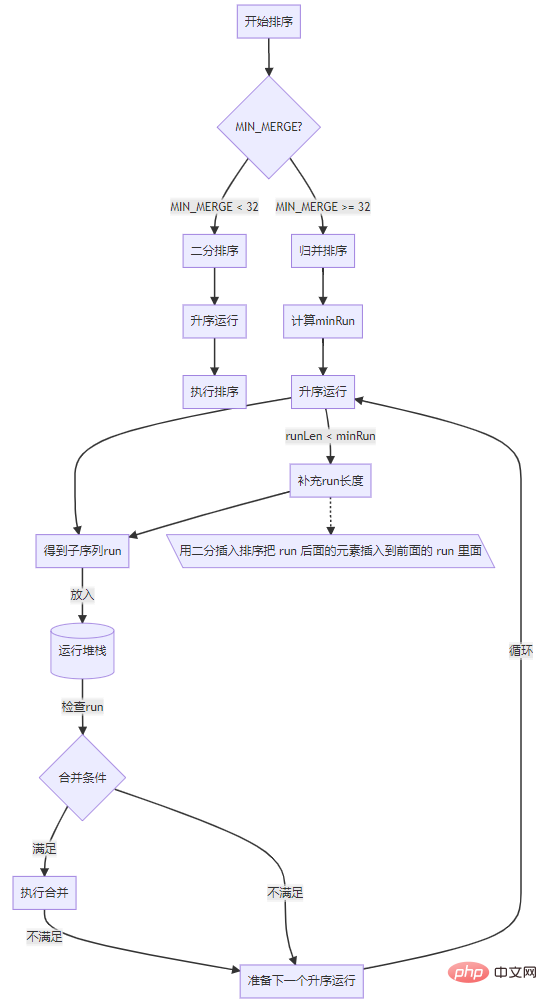
运行合并

当栈里面的 run 满足合并条件时，它就将栈里面相邻的两个run 进行合并。

合并条件

Timsort 为了执行平衡合并（让合并的 run 大小尽可能相同），制定了一个合并规则，对于在栈顶的三个run，分别用X、Y 和 Z 表示他们的长度，其中 X 在栈顶，它们必须始终维持一下的两个规则：

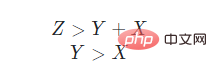
一旦有其中的一个条件不被满足，则将 Y 与 X 或 Z 中的较小者合并生成新的 run，并再次检查栈顶是否仍然满足条件。如果不满足则会继续进行合并，直至栈顶的三个元素都满足这两个条件，如果只剩两个run，则满足 Y > X 即可。

如下下图例子

• 当 Z <= Y+X ，将 X+Y 合并，此时只剩下两个run。

• 检测 Y < X ，执行合并，此时只剩下 X，则退出合并检测。

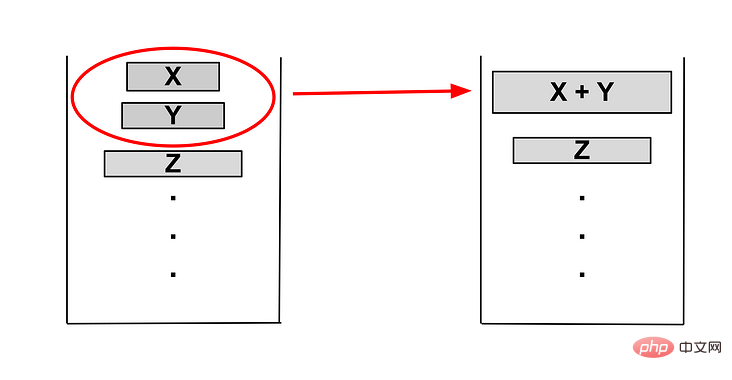
我们看下 Java 里面的合并实现

private void mergeCollapse() {
      
       // 当存在两个以上run执行合并检查
        while (stackSize > 1) {

          // 表示 Y
            int n = stackSize - 2; 
           
          // Z <= Y + X 
            if (n > 0 && runLen[n-1] <= runLen[n] + runLen[n+1]) { 

              // 如果 Z < X 合并Z+Y ，否则合并X+Y
              if (runLen[n - 1] < runLen[n + 1])
                    n--;
                
                // 合并相邻的两个run，也就是runLen[n] 和 runLen[n+1]
                mergeAt(n); 
            } else if (runLen[n] <= runLen[n + 1]) {
                
                // Y <= X 合并 Y+X
                mergeAt(n);
            } else {
                
                // 满足两个条件，跳出循环
                break; 
            }
        }
    }

合并内存开销

原始归并排序空间复杂度是 O(n)也就是数据大小。为了实现中间项，Timsort 进行了一次归并排序，时间开销和空间开销都比 O(n)小。

优化是为了尽可能减少数据移动，占用更少的临时内存，先找出需要移动的元素，然后将较小序列复制到临时内存，在按最终顺序排序并填充到组合序列中。

比如我们需要合并 X [1, 2, 3, 6, 10] 和 Y [4, 5, 7, 9, 12, 14, 17]，X 中最大元素是10，我们可以通过二分查找确定，它需要插入到 Y 的第 5个位置才能保证顺序，而 Y 中最小元素是4，它需要插入到 X 中的第4个位置才能保证顺序，那么就知道了[1, 2, 3] 和 [12, 14, 17] 不需要移动，我们只需要移动 [6, 10] 和 [4, 5, 7, 9]，然后只需要分配一个大小为 2 临时存储就可以了。

合并优化

在归并排序算法中合并两个数组需要一一比较每个元素，为了优化合并的过程，设定了一个阈值 MIN_GALLOP，当B中元素向A合并时，如果A中连续 MIN_GALLOP 个元素比B中某一个元素要小，那么就进入GALLOP模式。

根据基准测试，比如当A中连续7个以上元素比B中某一元素小时切入该模式效果才好，所以初始值为7。

当进入GALLOP模式后，搜索算法变为指数搜索，分为两个步骤，比如想确定 A 中元素x在 B 中确定的位置

• 首先在 B 中找到合适的索引区间(2^k−1,2^k+1−1) 使得 x 元素在这个范围内；

• 然后在第一步找到的范围内通过二分搜索来找到对应的位置。

只有当一次运行的初始元素不是另一次运行的前七个元素之一时，驰骋才是有益的。这意味着初始阈值为 7。

以上がJava での Timsort ソート アルゴリズムの手順と実装の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。