新しい研究により、量子モンテカルロが限界を突破する際にニューラルネットワークを超える可能性が明らかになり、Nature のサブ号で最新の進歩が詳しく説明されています

4 か月後、ByteDance Research と北京大学物理学部の Chen Ji の研究グループとの間の別の共同研究が、主要な国際出版物 Nature Communications に掲載されました。論文「##」 #ニューラル ネットワーク上の拡散モンテカルロ法による分子の基底状態の解明に向けて >>ニューラル ネットワークと拡散モンテカルロ法を組み合わせ、量子化学関連タスクにおけるニューラル ネットワーク法の計算精度、効率、システム規模を大幅に向上させます。 、最新のSOTAになります。

• 論文リンク:
  https://www.nature.com/articles/s41467-023-37609-3
コードアドレス:
• 
  ## https://github.com/bytedance/jaqmc ##はじめに
#著者は、ニューラル ネットワークに基づく試行波動関数を固定節点表面の拡散モンテカルロ法 (拡散モンテカルロ、または DMC) に適用して、さまざまな電子特性を持つ原子および分子システムを正確に計算します。

拡散モンテカルロ法は、分子や材料の基底状態エネルギーを正確に計算するために量子化学の分野で一般的に使用される方法の 1 つです。著者らは、これを拡散モンテカルロ法と組み合わせることで、量子化学におけるニューラル ネットワーク SOTA 法の計算精度と効率を大幅に向上させました。さらに、著者は経験的な線形関係に基づく外挿法も提案し、これにより分子結合エネルギーの計算が大幅に改善されました。全体として、この計算フレームワークは、量子多体問題を解決するための高精度な方法として機能し、化学分子の特性を深く理解するためのより強力なツールを提供します。

ニューラル ネットワークに基づく量子モンテカルロ法

2018 年以来、複数の研究グループがニューラル ネットワークを変分変数に適用してきました。モンテカルロ法 (変分モンテカルロ、または VMC) [1,2,3] では、ニューラル ネットワークの強力な表現能力を利用して、より正確な分子基底状態エネルギーが取得されます。この研究が 2022 年に発表されたとき、ニューラル ネットワーク ベースの変分モンテカルロ法における SOTA の研究は、2019 年に DeepMind によって提案された FermiNet [2] であり、より小規模なシステムで非常に正確な結果を得ることができました。ただし、変分モンテカルロ法の精度はニューラル ネットワークの表現能力によって制限され、大規模なシステムを扱う場合には精度の問題がますます明らかになります。さらに、このタイプの方法は、大規模なシステムを扱う場合には収束が非常に遅く、コンピューティング リソースに大きな課題をもたらします。

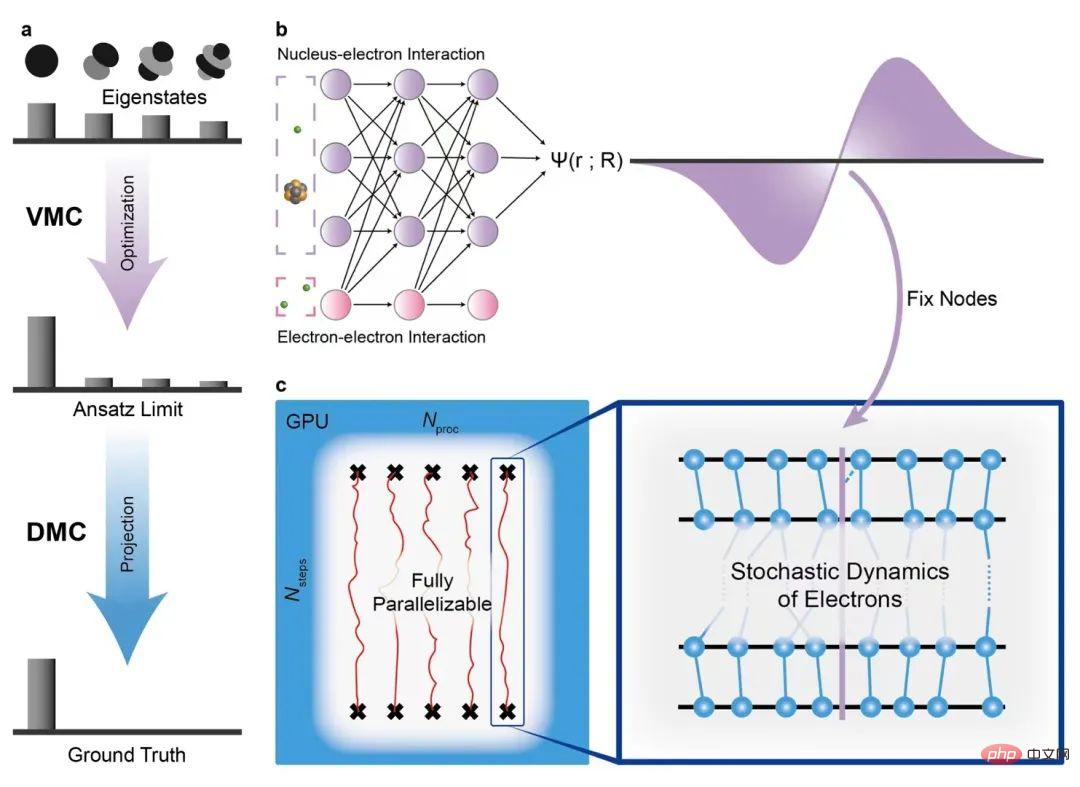
拡散モンテカルロ法は、量子化学分野における古典的な高精度アルゴリズムの一つであり、高精度、良好な並列性などの優れた特徴を持ち、大規模な計算に適しています。 -スケール計算。さらに、拡散モンテカルロはニューラル ネットワークの表現能力の限界を突破し、射影アルゴリズムを使用して変分モンテカルロ法の精度を超えることができます。

この研究では、著者は試行波動関数として SOTA のニューラル ネットワーク (FermiNet) を拡散モンテカルロ法と組み合わせます。新しい計算方法により、FermiNet と比較して精度が大幅に向上し、必要な計算ステップ数が削減されます。この研究で設計および実装された拡散モンテカルロ ソフトウェアは、ニューラル ネットワーク、GPU、並列に適しており、さまざまなニューラル ネットワークの波動関数と組み合わせて、精度と効率を自動的に向上させることができます。

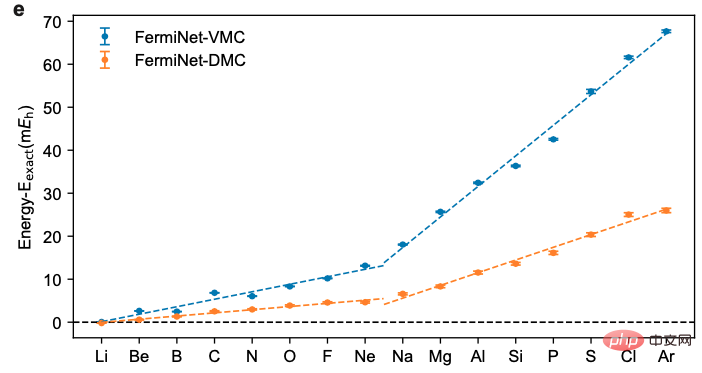
計算結果

1. Atom

ニューラルネットワークを使用して大規模な計算を実行分子システム 量子モンテカルロ計算中は、計算能力の制限により、使用できるニューラル ネットワークの表現能力にも一定の制限がかかります。このシナリオをシミュレートするために、著者らは 2 層のニューラル ネットワークのみを使用して、原子の 2 列目と 3 列目を研究しました。計算結果は、システムが大きくなるにつれて変分モンテカルロ法の精度がどんどん悪くなるのに対し、拡散モンテカルロ法の精度向上がますます顕著になることを示しています。

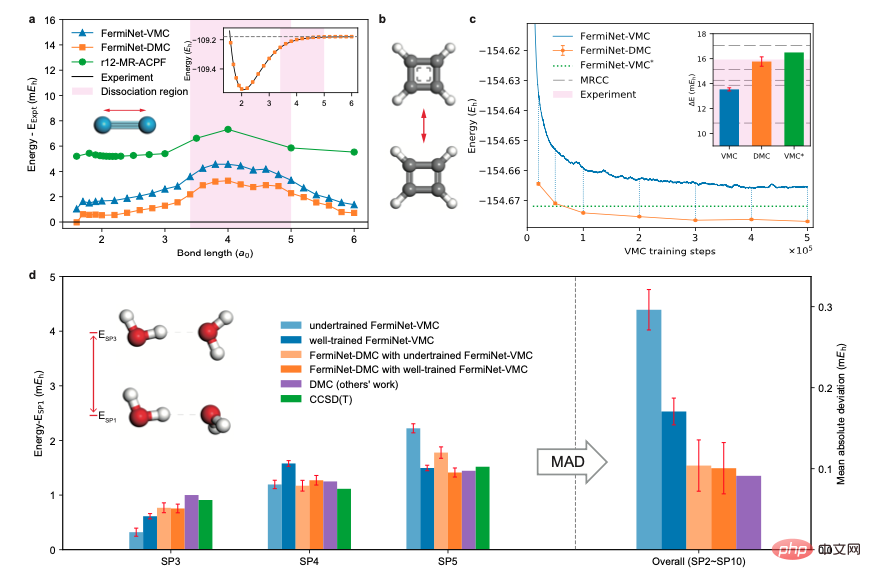
2. 分子

著者はまた、窒素分子、シクロブタジエン、二重水分子を含む一連の分子系に対するニューラル ネットワーク ベースの拡散モンテカルロ法の有効性を検証しました。テストしたすべてのシステムで、計算精度の大幅な向上が観察されました。

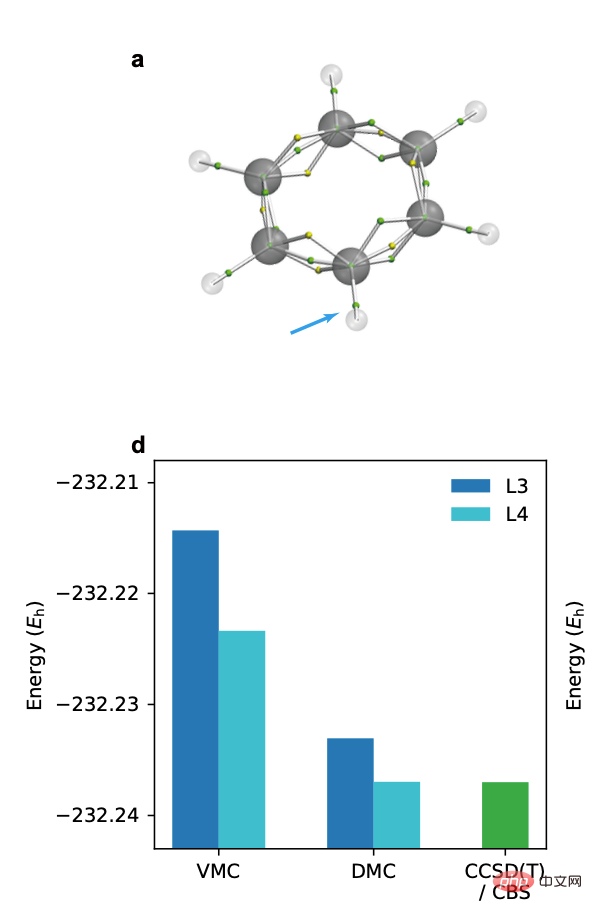
3. ベンゼン環とビフェニル環

この作品の前その出版物では、量子化学の分野における変分モンテカルロに基づくニューラル ネットワーク波動関数法は、電子 30 個以内の小さな分子しか扱っていませんでした。この研究では、ニューラルネットワーク波動関数法を電子数 42 ～ 84 個の系、つまりベンゼン環とビフェニル環に初めて適用しました。計算結果は、拡散モンテカルロ法が変分モンテカルロ法よりも精度が大幅に優れており、1桁少ない計算ステップで同等以上の精度を達成できることを示しています。

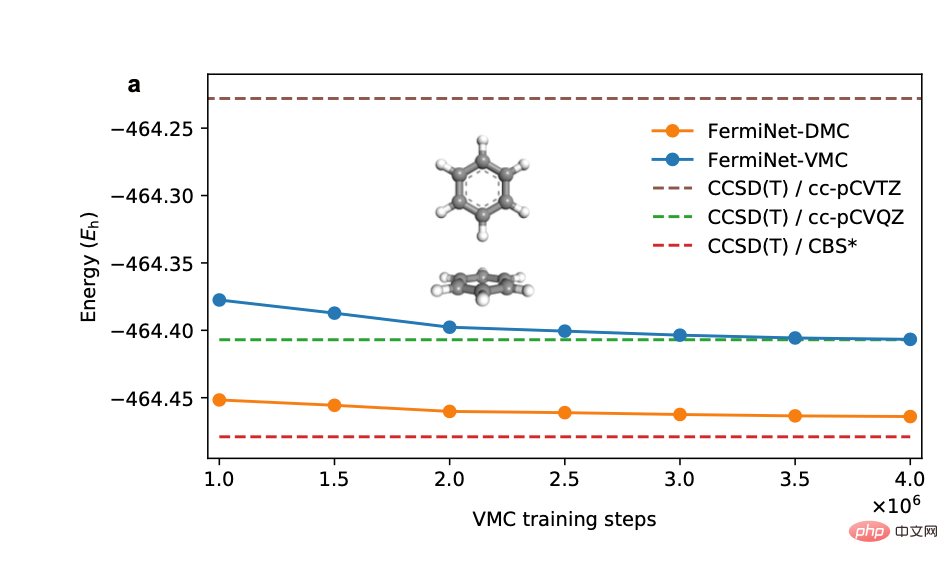
4. 線形関係と外挿方法

#著者がニューラル ネットワークのさまざまなトレーニング ステージに対応するエネルギーを調べたところ、変分モンテカルロと拡散モンテカルロの計算結果が多くのシステムで経験的であることがわかりました。線形関係 (下の左の写真）。この線形関係を使用してジフェニル環の解離エネルギー計算を外挿すると、計算精度が大幅に向上し、化学実験と一致する結果が得られます (下の右の図)。

#結論と展望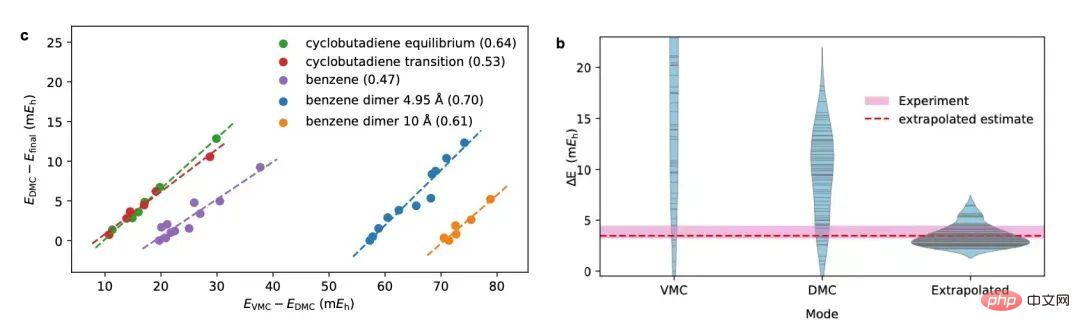

この研究は、ニューラル ネットワークに基づく拡散モンテカルロ法が精度と効率の両方で優れていることを示しています。 . 変分モンテカルロ法の場合。著者のオープンソースの拡散モンテカルロ コードは、量子化学の分野で常に革新的なニューラル ネットワーク [4,5] とすぐに組み合わせることができ、研究コミュニティに力を与えることができます。さらに、拡散モンテカルロ法は、周期的ニューラル ネットワーク [6] や実際の固体を扱う擬ポテンシャルを備えたニューラル ネットワーク [7] などの一連の手法と組み合わせて、対応するタスクの計算効果を向上させることもできます。

以上が新しい研究により、量子モンテカルロが限界を突破する際にニューラルネットワークを超える可能性が明らかになり、Nature のサブ号で最新の進歩が詳しく説明されていますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。