Java二分探索ツリーの追加・挿入・削除・作成例を詳しく解説
①概念
二分探索ツリーは二分ソート ツリーとも呼ばれ、空のツリー**、または次のプロパティを持ちます。バイナリ ツリー:
左側のサブツリーが空でない場合、左側のサブツリー上のすべてのノードの値はルート ノードの値より小さくなります。
右側のサブツリーが空でない場合、その値は右側のサブツリー上のすべてのノードの値がルート ノードの値より大きい
その左右のサブツリーも二分探索木です

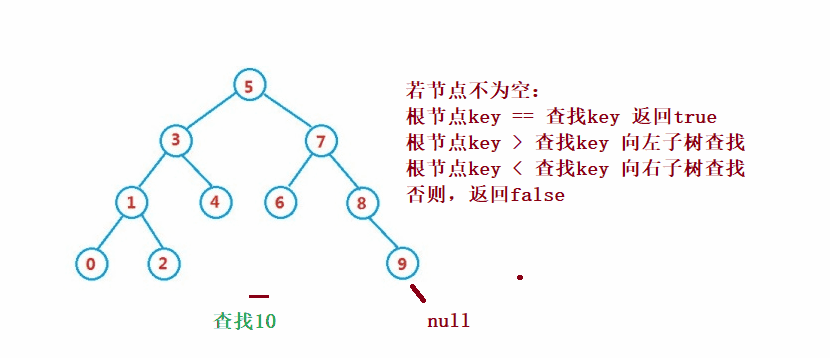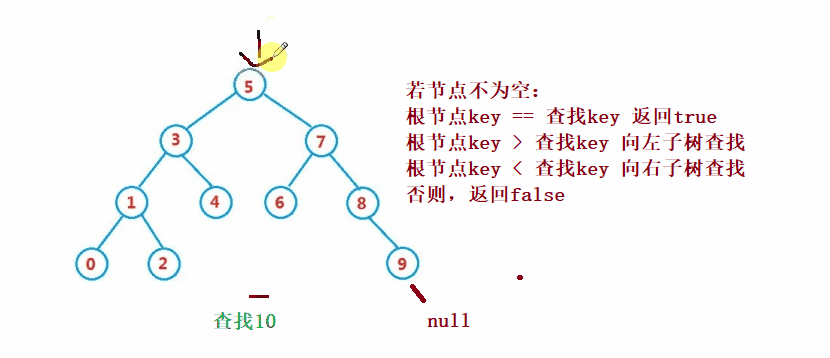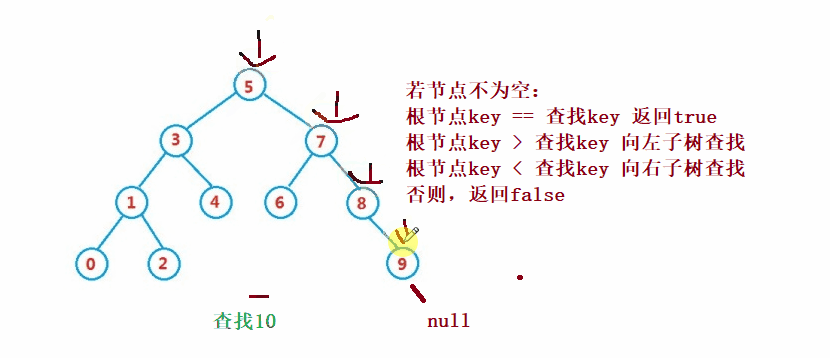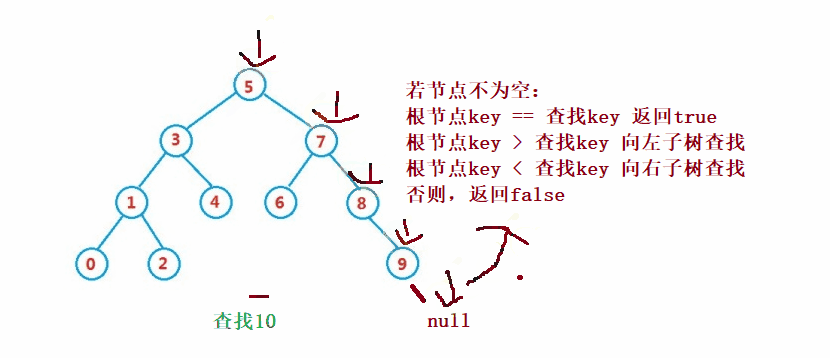
②操作- 検索
二分探索ツリー検索は二分探索と似ています


public Node search(int key) {
Node cur = root;
while (cur != null) {
if(cur.val == key) {
return cur;
}else if(cur.val < key) {
cur = cur.right;
}else {
cur = cur.left;
}
}
return null;
}


#
public boolean insert(int key) {
Node node = new Node(key);
if(root == null) {
root = node;
return true;
}
Node cur = root;
Node parent = null;
while(cur != null) {
if(cur.val == key) {
return false;
}else if(cur.val < key) {
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
//parent
if(parent.val > key) {
parent.left = node;
}else {
parent.right = node;
}
return true;
}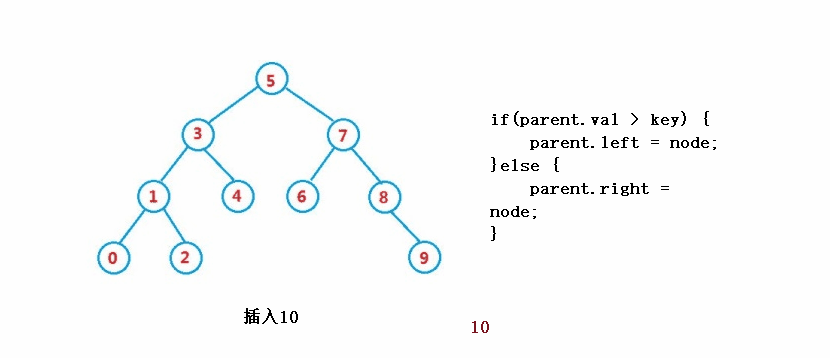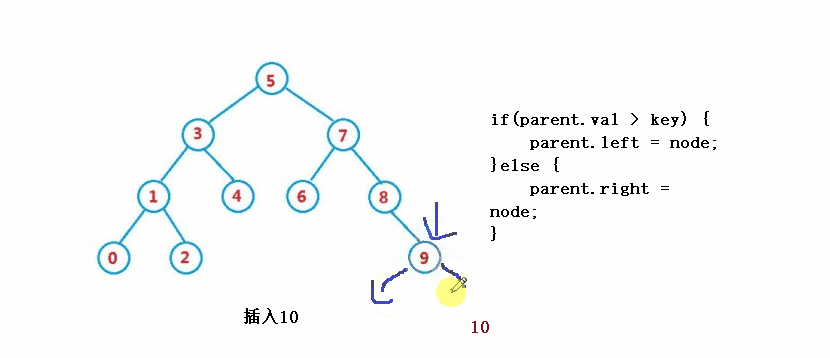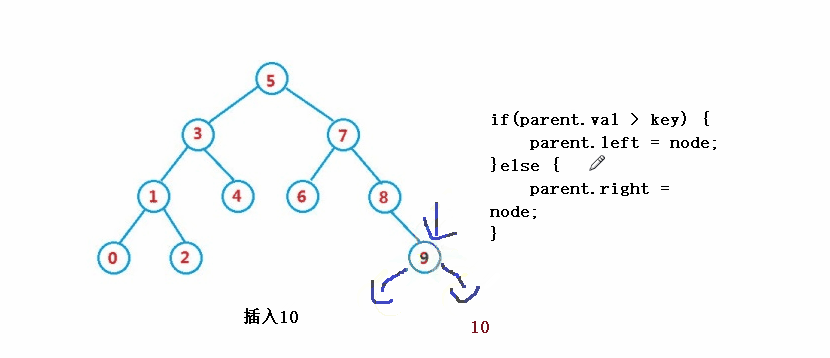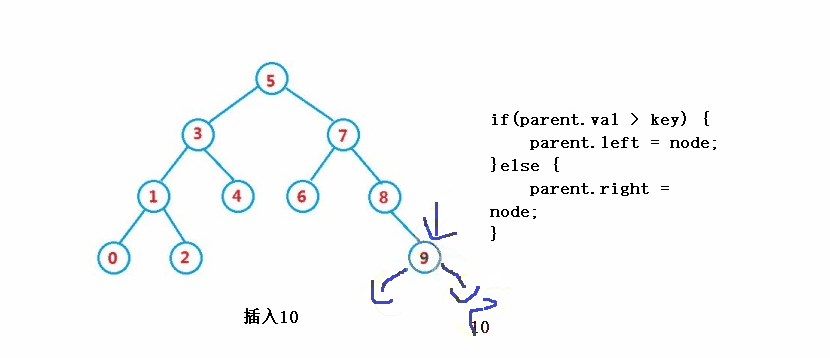 ④ 操作 - 削除
④ 操作 - 削除削除操作は比較的複雑ですが、その原理を理解するのは比較的簡単です。
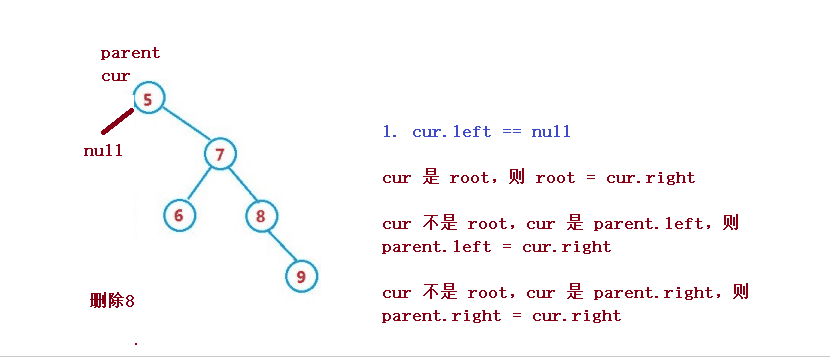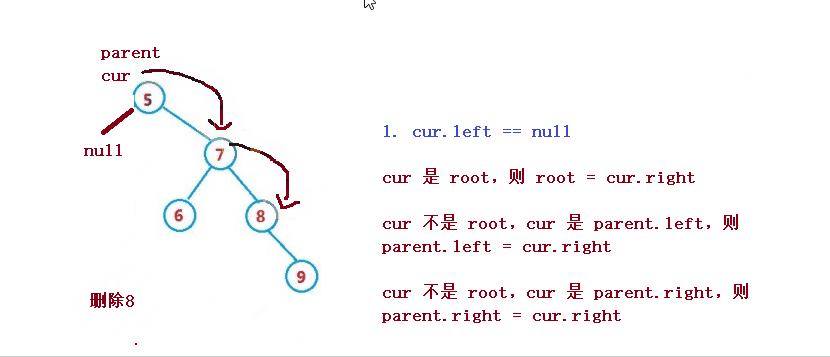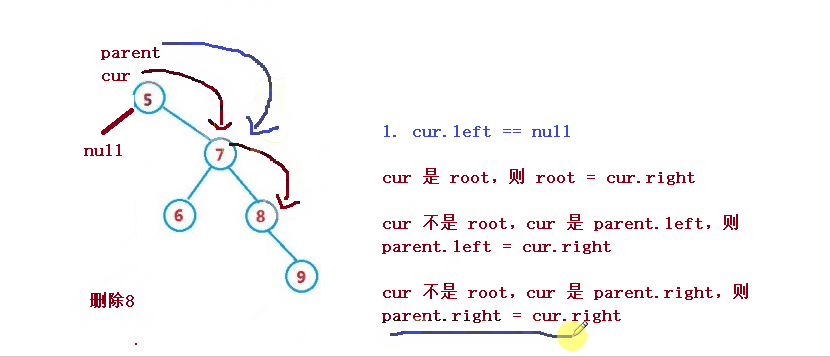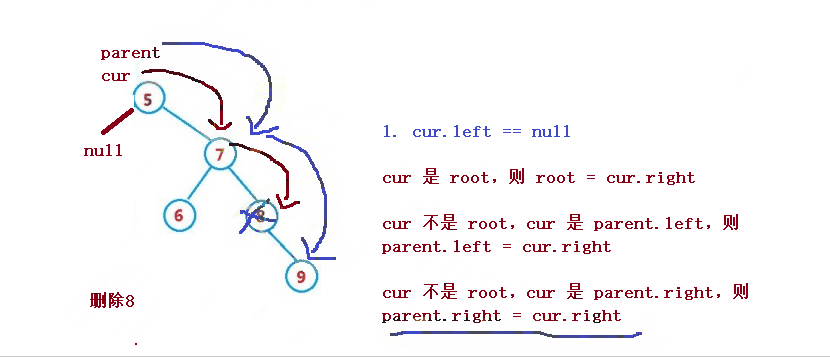
削除するノードを cur とし、削除するノードの親ノードをparentとする
1. cur.left == null
1. cur は root、次に root = cur.right
2. cur は root ではない、cur はparent.left、そして親.left = cur.right
3. cur は root ではなく、cur はparent.rightであり、parent.right = cur.right



 2. cur.right == null
2. cur.right == null
1. cur が root の場合、root = cur.left
2. Cur は root ではありません、cur はparent.left、その場合はparent.left = cur.left
3. Curはrootではありません、curはparent.right、その後はparent.rightです= cur.left
2 番目のケースは、方向が逆であることを除いて最初のケースと同じであり、ここではこれ以上描画しません
3. cur.left != null && cur.right ! = null
削除するには置換メソッドを使用する必要があります。つまり、右側のサブツリーで中間の順序の最初のノード (最小のキー コード) を見つけ、その値を削除されたノードに埋めます。ノードの削除の問題
左右のサブツリーが両方とも空のときにノードを削除すると、ツリーの構造が破壊されてしまうため、スケープゴート法を使用して解決します。この場合、バイナリツリー検索のプロパティがここでも使用されます


#
public void remove(Node parent,Node cur) {
if(cur.left == null) {
if(cur == root) {
root = cur.right;
}else if(cur == parent.left) {
parent.left = cur.right;
}else {
parent.right = cur.right;
}
}else if(cur.right == null) {
if(cur == root) {
root = cur.left;
}else if(cur == parent.left) {
parent.left = cur.left;
}else {
parent.right = cur.left;
}
}else {
Node targetParent = cur;
Node target = cur.right;
while (target.left != null) {
targetParent = target;
target = target.left;
}
cur.val = target.val;
if(target == targetParent.left) {
targetParent.left = target.right;
}else {
targetParent.right = target.right;
}
}
}
public void removeKey(int key) {
if(root == null) {
return;
}
Node cur = root;
Node parent = null;
while (cur != null) {
if(cur.val == key) {
remove(parent,cur);
return;
}else if(cur.val < key){
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
} ⑤パフォーマンス分析
⑤パフォーマンス分析 挿入操作と削除操作の両方を最初に検索する必要があります。検索効率は、二分探索ツリー内の各操作のパフォーマンスを表します。
n 個のノードを持つ二分探索木の場合、各要素の検索確率が等しい場合、二分探索木の平均検索長は二分探索木のノードの深さの関数になります。つまり、ノードです。ポイントが深くなるほど、より多くの比較が行われます。
しかし、同じキー コード セットに対して、キー コードが異なる順序で挿入されると、異なる構造を持つ二分探索木が取得される可能性があります。
最適な場合、二分探索木は二分木の場合、平均比較数は次のとおりです。
 最悪の場合、二分探索木は単一の分岐木に縮退し、平均比較数は次のとおりです。比較は:
最悪の場合、二分探索木は単一の分岐木に縮退し、平均比較数は次のとおりです。比較は:
⑥完整代码
public class TextDemo {
public static class Node {
public int val;
public Node left;
public Node right;
public Node (int val) {
this.val = val;
}
}
public Node root;
/**
* 查找
* @param key
*/
public Node search(int key) {
Node cur = root;
while (cur != null) {
if(cur.val == key) {
return cur;
}else if(cur.val < key) {
cur = cur.right;
}else {
cur = cur.left;
}
}
return null;
}
/**
*
* @param key
* @return
*/
public boolean insert(int key) {
Node node = new Node(key);
if(root == null) {
root = node;
return true;
}
Node cur = root;
Node parent = null;
while(cur != null) {
if(cur.val == key) {
return false;
}else if(cur.val < key) {
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
//parent
if(parent.val > key) {
parent.left = node;
}else {
parent.right = node;
}
return true;
}
public void remove(Node parent,Node cur) {
if(cur.left == null) {
if(cur == root) {
root = cur.right;
}else if(cur == parent.left) {
parent.left = cur.right;
}else {
parent.right = cur.right;
}
}else if(cur.right == null) {
if(cur == root) {
root = cur.left;
}else if(cur == parent.left) {
parent.left = cur.left;
}else {
parent.right = cur.left;
}
}else {
Node targetParent = cur;
Node target = cur.right;
while (target.left != null) {
targetParent = target;
target = target.left;
}
cur.val = target.val;
if(target == targetParent.left) {
targetParent.left = target.right;
}else {
targetParent.right = target.right;
}
}
}
public void removeKey(int key) {
if(root == null) {
return;
}
Node cur = root;
Node parent = null;
while (cur != null) {
if(cur.val == key) {
remove(parent,cur);
return;
}else if(cur.val < key){
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
}
}以上がJava二分探索ツリーの追加・挿入・削除・作成例を詳しく解説の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7458
7458
 15
15
 1376
1376
 52
52
 77
77
 11
11
 17
17
 17
17
 Javaのアームストロング数
Aug 30, 2024 pm 04:26 PM
Javaのアームストロング数
Aug 30, 2024 pm 04:26 PM
Java のアームストロング番号に関するガイド。ここでは、Java でのアームストロング数の概要とコードの一部について説明します。
 Java の乱数ジェネレーター
Aug 30, 2024 pm 04:27 PM
Java の乱数ジェネレーター
Aug 30, 2024 pm 04:27 PM
Java の乱数ジェネレーターのガイド。ここでは、Java の関数について例を挙げて説明し、2 つの異なるジェネレーターについて例を挙げて説明します。
 ジャワのウェカ
Aug 30, 2024 pm 04:28 PM
ジャワのウェカ
Aug 30, 2024 pm 04:28 PM
Java の Weka へのガイド。ここでは、weka java の概要、使い方、プラットフォームの種類、利点について例を交えて説明します。
 Java Springのインタビューの質問
Aug 30, 2024 pm 04:29 PM
Java Springのインタビューの質問
Aug 30, 2024 pm 04:29 PM
この記事では、Java Spring の面接で最もよく聞かれる質問とその詳細な回答をまとめました。面接を突破できるように。
 Java 8 Stream Foreachから休憩または戻ってきますか?
Feb 07, 2025 pm 12:09 PM
Java 8 Stream Foreachから休憩または戻ってきますか?
Feb 07, 2025 pm 12:09 PM
Java 8は、Stream APIを導入し、データ収集を処理する強力で表現力のある方法を提供します。ただし、ストリームを使用する際の一般的な質問は次のとおりです。 従来のループにより、早期の中断やリターンが可能になりますが、StreamのForeachメソッドはこの方法を直接サポートしていません。この記事では、理由を説明し、ストリーム処理システムに早期終了を実装するための代替方法を調査します。 さらに読み取り:JavaストリームAPIの改善 ストリームを理解してください Foreachメソッドは、ストリーム内の各要素で1つの操作を実行する端末操作です。その設計意図はです







