Javaで最小高さのツリーを実装する方法

質問要件

ツリーは、任意の 2 つの頂点が 1 つのパスのみで接続されている無向グラフです。言い換えれば、単純なサイクルを持たない接続されたグラフはすべてツリーです。

あなたには、 0 から n - 1 までのラベルが付けられた n 個のノードを含むツリーが与えられます。数値 n と、n - 1 個の無向エッジ (各エッジはラベルのペア) を含むエッジ リストが与えられると、edges[i] = [ai, bi] は、ツリー内のノード ai と bi の間にエッジがあることを意味します。角。

ツリー内の任意のノードをルートとして選択できます。ノード x がルート ノードとして選択された場合、結果ツリーの高さを h とします。すべての可能なツリーの中で、最小の高さ (つまり、 min(h)) を持つツリーを、 最小高さのツリー と呼びます。

すべての最小高さのツリーを検索し、そのルート ノード ラベル リストを任意の順序で返してください。

ツリーの高さは、ルート ノードとリーフ ノードの間の最長の下向きパス上のエッジの数を指します。

例 1:

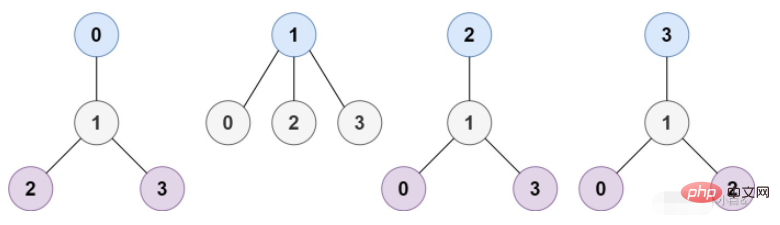
入力: n = 4、エッジ = [[1,0],[1,2],[1,3] ]
出力: [1]
説明: 図に示すように、ルートがラベル 1 のノードである場合、ツリーの高さは 1 であり、これが唯一の最小高さのツリーです。

例 2:

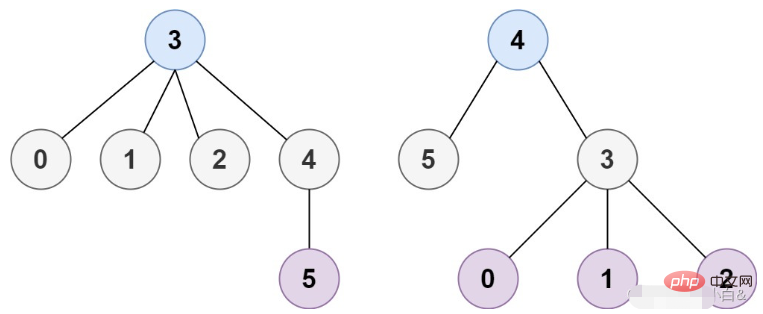
入力: n = 6、エッジ = [[3,0],[3,1],[3] ,2],[3,4],[5,4]]
出力: [3,4]

##プロンプト:

1 edges.length == n - 1
0 ai != bi
すべて (ai, bi) は互いに異なります
指定された入力はツリーであることが保証されており、重複するエッジは存在しません

問題解決のアイデア

  上記の 2 つのグラフから、次のように描画できます。結論: この問題で解決する必要があるのはツリー内の中心ノードであり、各ツリーには 2 つ以下の中心ノードがあります。

  そして、ツリー内の中心ノードを取得したい場合は、FBS をレイヤーごとに使用できます (つまり、レイヤーごとに 1 つの出力次数でリーフ ノードを切り取ります)。最後のレイヤーがカットされるまで、結果を出力できます。

アルゴリズム

class Solution {
    public List<Integer> findMinHeightTrees(int n, int[][] edges) {
        List<Integer> res = new ArrayList<Integer>();
        //如果只有一个节点，则它就是最小高度树
        if(n == 1){
            res.add(0);
            return res;
        }

        //每个节点的邻居数量
        int [] degree = new int[n];
        //每个节点的邻居
        HashMap<Integer,List<Integer>> map = new HashMap<>();

        for(int [] edge : edges){
            int a = edge[0];
            int b = edge[1];

            degree[a]++;
            degree[b]++;

            if(map.get(a) == null){
                map.put(a,new ArrayList<Integer>());//key:节点   value:邻居
            }

            if(map.get(b) == null){
                map.put(b,new ArrayList<Integer>());//key:节点   value:邻居
            }

            map.get(a).add(b);
            map.get(b).add(a);
        }

        //建立队列
        LinkedList<Integer> leafNodes = new LinkedList<Integer>();//表示叶子节点
        //将所有度为1的节点入队
        for(int i = 0;i < degree.length;i++){
            if(degree[i] == 1){
                leafNodes.add(i);
            }
        }

        while(leafNodes.size() > 0){
            res.clear();
            //每一层节点的数量
            int size = leafNodes.size();

            for(int i = 0;i < size;i++){
                int leaf = leafNodes.poll();
                //将当前节点加入到结果集
                res.add(leaf);

                List<Integer> neighbors = map.get(leaf);
                //将出度减一，也就是将最外层的叶子节点剪掉
                for(int neighbor : neighbors){
                    degree[neighbor]--;
                    if(degree[neighbor] == 1){
                        //叶子节点入队
                        leafNodes.add(neighbor);
                    }
                }
            }
        }
        return res;
    }
}

以上がJavaで最小高さのツリーを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。