Google の研究では、数学的問題をコードに変換することで、機械証明の精度が大幅に向上しました。

数学的証明の検証にはコンピュータがしばらく使用されてきましたが、それができるのは特別に設計された証明言語を使用して問題が準備されている場合に限られ、数学的表記と数学者が使用する記述テキストの混合を処理できませんでした。

自然言語で書かれた数学的問題を正式なコードに変換し、コンピューターが解決しやすくすれば、数学の新たな発見を探索できるマシンの構築に役立つ可能性があります。

このプロセスは形式化と呼ばれますが、たった 1 つの証明に何年もかかる場合があるため、数学的知識のごく一部のみが形式化され、機械によって証明されます。

自動形式化とは、数学を自然言語から形式言語に自動的に変換するタスクを指します。自動化された形式化ツールが成功すれば、実用的かつ哲学的な意味合いは計り知れず、現在の過剰な形式化コストを削減できる可能性があり、長期的にはさまざまな研究分野で数学的推論の自動化された側面を結び付けることができるでしょう。

最近の研究では、Google の Yuhuai Wu 氏とその共同研究者は、OpenAI Codex のニューラル ネットワークを使用して形式化作業を自動化しました。 Codex は Web からの大量のテキストとプログラミング データでトレーニングされており、プログラマーはこれを使用して信頼性の高いコードを生成できます。

#論文リンク: https://arxiv.org/pdf/2205.12615.pdf

12,500 の中学校数学コンテストの問題を形式化

#大規模言語モデルにおける最近の一連の進歩は、形式言語を理解するためのモデルの可能性を実証しています。ただし、これまでの成功例は、Web 上に大規模なコーパスが存在する形式言語 (Python など) に限られていました。対照的に、正式な数学データは非常に不足しており、最大規模の正式な数学言語ライブラリの 1 つである Archive of Formal Proofs のサイズはわずか 180 MB であり、大規模言語モデル Codex のトレーニング データの 0.18% 未満です。

さらに、自然言語の docstring が広く利用できる汎用プログラミング言語の場合とは異なり、自然言語と形式数学言語の間ではデータの整合性がほとんどありません。したがって、大規模言語モデルの成功が自動形式化の開発を直接促進できるかどうかはまだ不明です。

証明言語とプログラミング言語の類似点を考慮して、チームは Codex が 12,500 の中学校数学コンテストの問題のライブラリを形式化できるかどうかを確認することにしました。問題の 4 分の 1 を、正式な証明ソルバー Isabelle と互換性のある形式に変換できます。

Wu 氏は、変換の失敗の多くは、システムが特定の数学的概念を理解していないことが原因であると述べました。 「概念を説明する例をモデルに示すと、モデルはそれをすぐに理解できるようになります。」

この研究では、大規模な言語モデルの自動形式化の可能性を探ります。研究者らは、大規模な言語モデルがすでに存在していることを発見しました。インタラクティブな定理証明器で自然言語数学を形式化するかなり優れた能力を持っています。

以下の図 1 は、自動形式化の完璧な例です。このモデルは、構文的に正しい Isabelle コードを変換するだけでなく、自然言語で重要な推論ポイントをキャプチャすることもできます。

この自動化された形式化プロセスの有効性をテストするために、チームは、人間が形式化したバージョンがすでに存在する一連の問題に Codex を適用しました。これに対して Codex も生成されました。独自の正式版。チームは、MiniF2F と呼ばれる別の AI を使用して、両方のバージョンの問題を解決しました。

問題を自動的に形式化すると、MiniF2F の成功率が 29% から 35% に増加しました。これは、Codex が問題の形式化において重要な進歩を遂げたことを示しています。

多くの数学コンテストでのプレゼンテーションは、特定の問題を証明するのではなく、特定の問題に対する答えを見つけることが求められるという形式になる傾向があることは注目に値します。命題。ただし、正式な数学的記述は質問ではなく命題の形式です。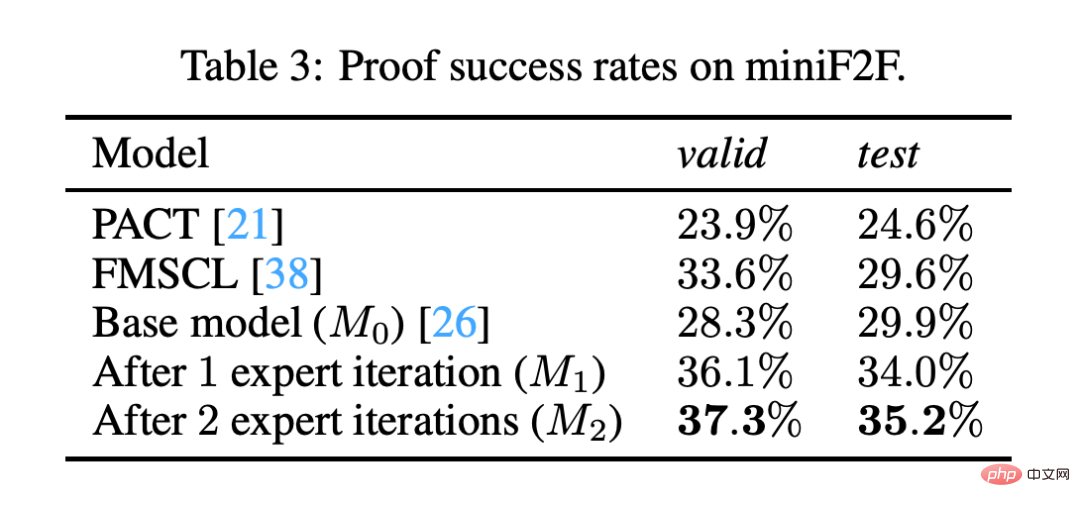

質問を命題に変換するために、研究者は質問の後に「最終回答」を添付しました。

自動形式化に使用されます。形式は次のとおりです:

#

AI は人間の数学者と競合するでしょうか?

これは興味深い開発ですが、ウー氏によると、 チームの作業は単なる概念実証です 。 「人間のトップの数学者に匹敵するマシンを訓練することが目標であるならば、自動形式化がこの目標を達成するための重要な道であるように思われます。」

ケンブリッジ大学チームのメンバーであるアルバート・ジャン氏は、成功率がさらに向上すれば、AI は人間の数学者と競争できるようになるでしょう。 "100% に到達したら、国際数学オリンピックの金メダルを獲得する AI エージェントを必ず作成します。"

チームの当面の目標は、自動形式モデルと自動化の Proof of を改善することです。しかし、研究結果の将来の影響ははるかに深刻になるでしょう。ウー氏は、これらのモデルは現在人間に知られていない数学の領域を明らかにできると述べています。

このマシンの推論機能は、より幅広い分野の検証タスクにも非常に適しています。 「ソフトウェアが希望どおりの動作をするかどうかを検証したり、ハードウェア チップを検証したりできるため、金融取引アルゴリズムやハードウェア設計に応用できます。」

マシンを使用して数学を探求することは、ロンドンの数理科学研究所のヤン・フイ・ヘ氏は、開発には興奮しているが、本当の課題は、主に LaTex で書かれたモデルを数学研究に使用することだと語ります。 「入力がスムーズであるという理由で LaTex を使用しているだけですが、LaTex はある意味で自然言語であり、独自のルールがあります。」

彼は、ユーザーが独自の関数と表記法を定義できるため、これらの関数と表記法を定義できると述べました。シンボルは 1 つの数学論文でのみ使用できますが、プレーン テキストのみで訓練されたニューラル ネットワークではこれが難しい場合があります。

以上がGoogle の研究では、数学的問題をコードに変換することで、機械証明の精度が大幅に向上しました。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。