多変量時系列における公平性の問題について

今日は、2023.1 に arixv に投稿された多変量時系列予測記事をご紹介します。出発点は非常に興味深いもので、多変量​​時系列の公平性を向上させる方法です。この記事で使用されているモデリング手法はすべて、時空予測やドメイン適応などで使用されている従来の操作ですが、多変数の公平性という点は比較的新しいものです。

#論文タイトル: 公平性を意識した多変量時系列予測のための有益な表現の学習: グループベースの視点
• ダウンロードアドレス: https://arxiv.org/pdf/2301.11535.pdf

1. 多変量時系列の公平性

公平性の問題、それは機械学習の分野におけるマクロの概念。機械学習における公平性の 1 つは、さまざまなサンプルに対するモデルのフィッティング効果の一貫性です。モデルが一部のサンプルでは良好なパフォーマンスを示し、他のサンプルではパフォーマンスが悪い場合、そのモデルは公平性が低くなります。たとえば、一般的なシナリオでは、レコメンデーション システムでは、先頭サンプルに対するモデルの予測効果が末尾サンプルに対する予測効果よりも優れており、これはさまざまなサンプルに対するモデルの予測効果の不公平さを反映しています。

多変量時系列予測の問題に戻ると、公平性とは、モデルが各変数に対してより良い予測効果を持つかどうかを指します。さまざまな変数に対するモデルの予測効果が大きく異なる場合、この多変量時系列予測モデルは不公平になります。例えば、下図の例では、表の1行目が各変数に対する各種モデルの予測効果のMAEの分散となっており、モデルごとにある程度の不公平性があることがわかります。下の図のシーケンスは一例であり、予測に優れたシーケンスもあれば、予測に劣るシーケンスもあります。

#2. 不公平の原因と解決策

なぜ不公平が起こるのか？多変量時系列であろうと他の機械学習分野であろうと、異なるサンプルの予測効果に大きな違いがある主な理由の 1 つは、異なるサンプルが異なる特性を持ち、トレーニング中にモデルが特定のサンプルの特性によって支配される可能性があることです。このモデルは、トレーニングを支配するサンプルについては適切に予測しますが、支配されていないサンプルについてはあまり予測しません。

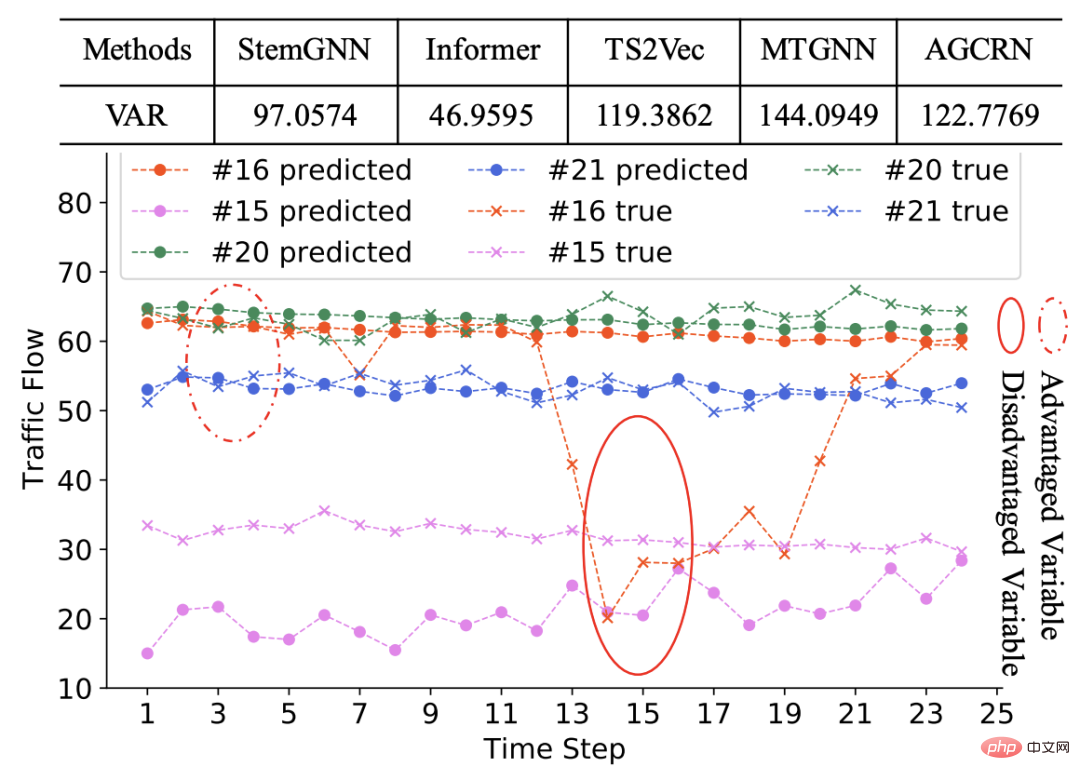
多変量時系列では、異なる変数が非常に異なるシーケンス パターンを持つ可能性があります。たとえば、上に示した例では、ほとんどのシーケンスは静止しており、これがモデルのトレーニング プロセスを支配しています。少数のシーケンスは他のシーケンスとは異なる変動性を示し、その結果、これらのシーケンスに対するモデルの予測パフォーマンスが低下します。

多変量時系列の不公平性を解決するにはどうすればよいでしょうか?一つの考え方として、不公平性は異なるシーケンスの特性の違いによって引き起こされるため、シーケンス間の共通点とシーケンス間の相違点を独立に分解してモデル化できれば、上記の問題を軽減できるのではないかという疑問が生じます。

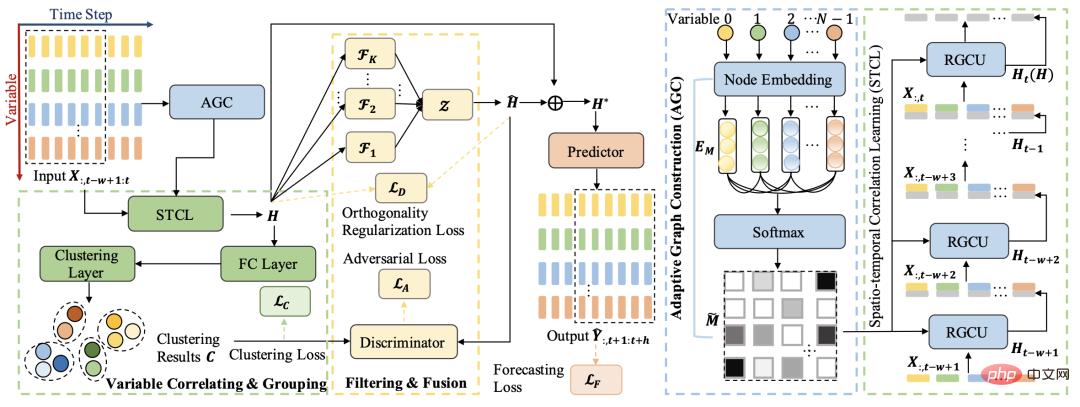
この記事はこの考えに基づいています。全体的なアーキテクチャは、クラスタリング手法を使用して多変数シーケンスをグループ化し、各グループの共通特徴を取得します。さらに、敵対的学習手法を使用して元の表現から学習します。 . 各グループに固有の情報を剥がして、共通の情報を取得します。上記のプロセスにより、公開情報と配列固有の情報が分離され、これら 2 つの情報に基づいて最終的な予測が行われます。

3. 実装の詳細

全体的なモデル構造には主に、多変数シーケンス関係学習、時空間関係ネットワーク、シーケンス クラスタリング、分解の 4 つのモジュールが含まれています。勉強。

多変量シーケンスの関係学習

多変量時系列の重要なポイントの 1 つは、各シーケンス間の関係を学習することです。この記事では、時空間法を使用してこの関係を学習します。多変量時系列は多くの時空間予測タスクとは異なり、さまざまな変数間の関係を事前に定義できるため、ここでは隣接行列の自動学習方法が使用されます。具体的な計算ロジックは、変数ごとにランダムに初期化された埋め込みを生成し、埋め込みの内積と後処理を使用して、隣接行列の対応する位置の要素として 2 つの変数間の関係を計算します。数式は次のとおりです。

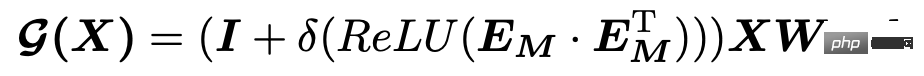隣接行列を自動的に学習するこの方法は、「Connecting the Dots: Multivariate Time Series Forecasting with Graph Neural Networks」の時空間予測で非常に一般的に使用されています。 (KDD 2020)、REST : このアプローチは、時空間結合予測のための相互フレームワーク (WWW 2021) などの論文で採用されています。関連するモデルの原理実装については、Planet の記事 KDD2020 古典時空予測モデル MTGNN コード分析で詳しく紹介していますので、興味のある方はさらに読んでください。

時空間関係ネットワーク

隣接行列を取得した後、この記事では、グラフ時系列予測モデルを使用して多変数時系列を時空間的にエンコードし、各変数シーケンスの表現を取得します。具体的なモデル構造は DCRNN と非常に似ており、GRU に基づいて各ユニットの計算に GCN モジュールが導入されています。通常の GRU の各ユニットの計算プロセスでは、隣接ノードのベクトルを導入して GCN を実行し、更新された表現を取得することがわかります。 DCRNN の実装コードの原則については、DCRNN モデルのソース コード分析に関するこの記事を参照してください。

シーケンス クラスタリング

各変数時系列の表現を取得した後の次のステップは、これらの表現をクラスタリングして各変数シーケンスのグループ化を取得し、各グループの固有の特性を抽出することです。変数の情報。この記事では、クラスタリング プロセスをガイドするために次の損失関数を導入します。ここで、H は各変数シーケンスの表現を表し、F は各変数シーケンスと K カテゴリへの所属を表します。

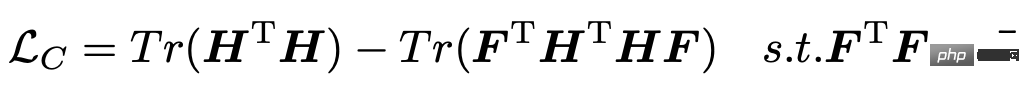
この損失関数の更新プロセスでは、EM アルゴリズムを使用する必要があります。つまり、H を表すシーケンスを固定して F を最適化し、F を固定して H を最適化します。この記事で採用された方法は、表現 H を取得するためにモデルを数回トレーニングした後、SVD を使用して行列 F を 1 回更新することです。

分解学習

分解学習モジュールの核心は、各カテゴリ変数のパブリック表現とプライベート表現を区別することです。パブリック表現とは、各クラスター変数のシーケンスによって共有される特性を指します、およびプライベート表現は、各クラスター内の変数シーケンスの固有の特性を指します。この目標を達成するために、この論文では、分解学習と敵対的学習のアイデアを採用して、元のシーケンス表現から各クラスターの表現を分離します。クラスタ表現は各クラスの特徴を表現し、ストリップ表現は全系列の共通性を表現し、この共通表現を用いて予測することで、各変数の予測の公平性を図ることができる。

この記事では、敵対的学習の考え方を利用して、パブリック表現とプライベート表現（つまり、クラスタリングによって得られる各クラスターの表現）の間の L2 距離を直接計算し、これを次のように使用します。損失を逆に最適化して公的部分を代表させる 私的代表とのギャップは可能な限り広い。さらに、パブリック表現とプライベート表現の内積を 0 に近づけるための直交制約が追加されます。

4. 実験結果

この記事の実験は、主に公平性と予測効果の 2 つの側面から比較され、比較されるモデルには、基本的な時系列予測モデル (LSTNet、Informer)、グラフ時間などが含まれますシリーズ予測モデルなど公平性に関しては、異なる変数の予測結果の分散を利用しており、比較すると他のモデルと比較して公平性が大幅に向上しています（下表参照）。

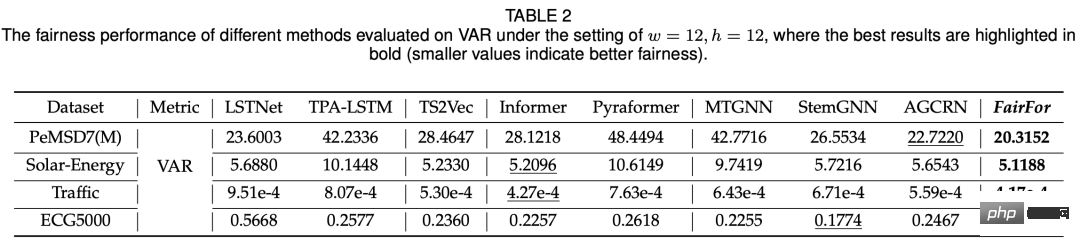
#予測効果の点では、この記事で提案するモデルは基本的に SOTA と同等の結果を達成できます。

#5 , 概要

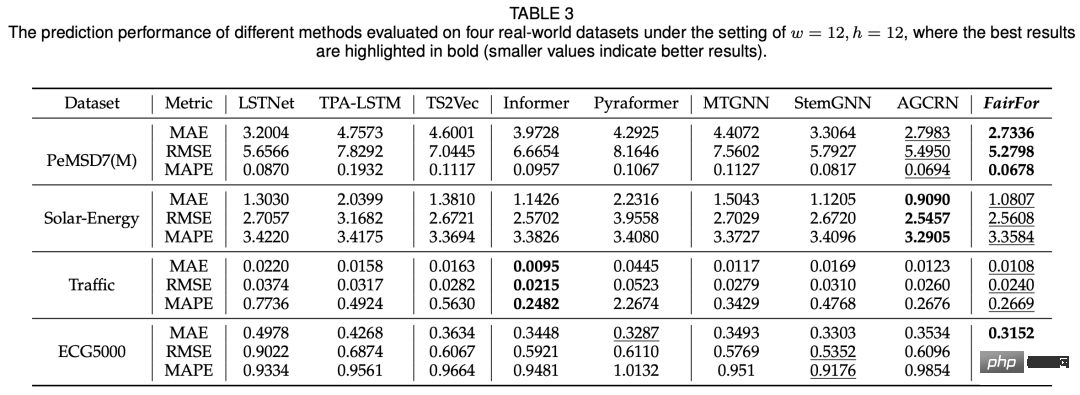
モデルの公平性を確保する方法は、機械学習の多くのシナリオが直面する問題です。この論文では、この次元の問題を多変量時系列予測に導入し、時空間予測と敵対的学習手法を使用して問題をより適切に解決します。

以上が多変量時系列における公平性の問題についての詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。