
まず、二分探索木とは何かについて補足説明を追加します。
二分探索木では、各ノードの左側のサブツリーの値はそれより小さく、右側のサブツリーの値はそれより大きくなります。したがって、二分探索ツリーの順序どおりの走査は、順序付けられたデータのセットです。
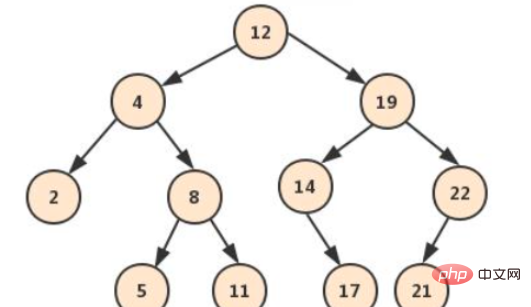
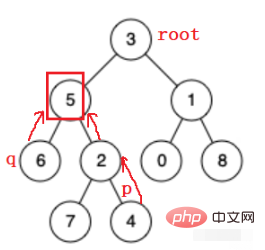
#上記のツリーでは、p q の最も近い共通祖先が必要であると仮定します。
その場合、次のような状況になります。
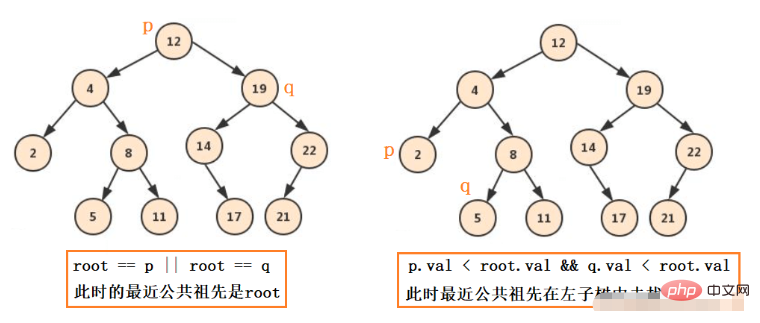
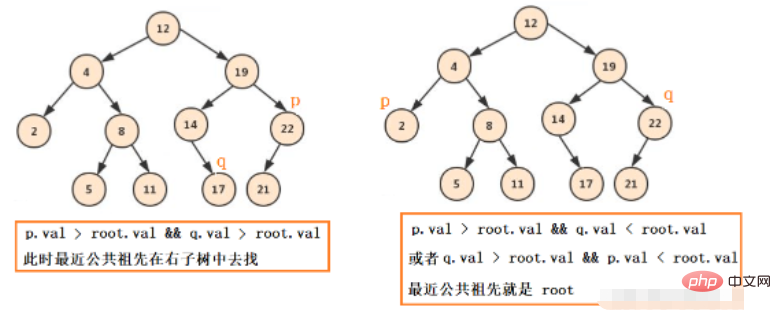
通常のバイナリ ツリーの場合、これらの状況以上のものはありません。 : pq はすべて左側にあり、pq はすべて右側にあり、pq は左側に 1 つと右側に 1 つあり、pq の 1 つはルート ノードです。
したがって、左のサブツリーと右のサブツリーに再帰的に移動して、p q ノードの共通の祖先を見つけます。見つかった場合はそのノードが返され、見つからなかった場合は空が返されます。
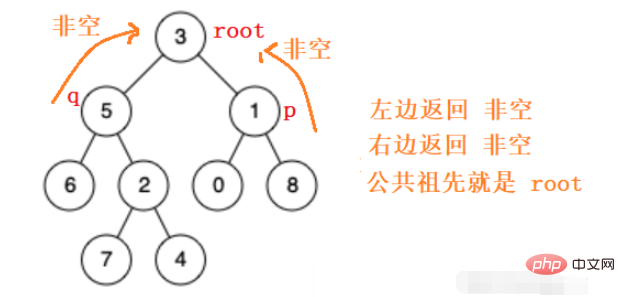
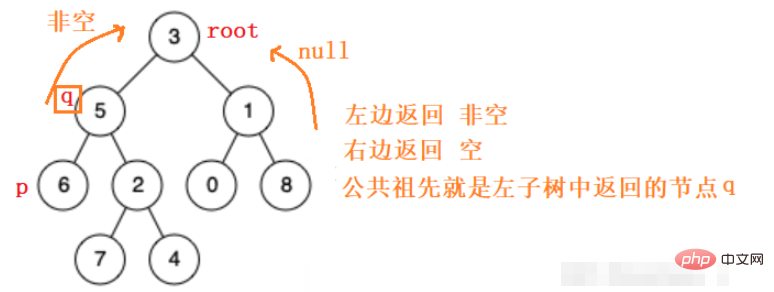
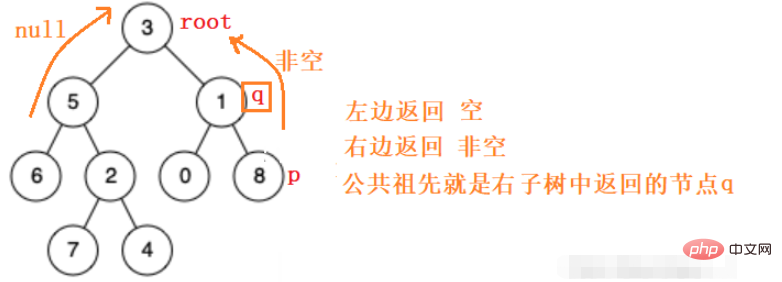
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null) return null;
// p 为当前树的根节点
if(p == root) return p;
// q 为当前树的根节点
if(q == root) return q;
// 去左子树中找
TreeNode left = lowestCommonAncestor(root.left,p,q);
// 去右子树中找
TreeNode right = lowestCommonAncestor(root.right,p,q);
// 左边右边都找到了
if(left != null && right != null) {
return root;
}
// 左边找到了,右边没找到
if(left != null) {
return left;
}
if(right != null) {
return right;
}
return null;
}
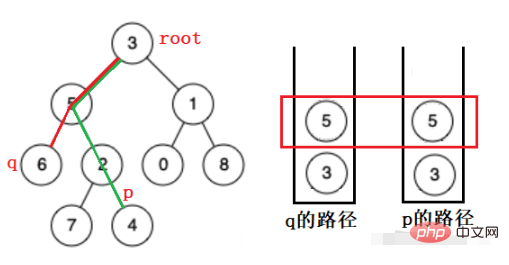 #ここでの最大の問題は、ストレージ パスです。
#ここでの最大の問題は、ストレージ パスです。
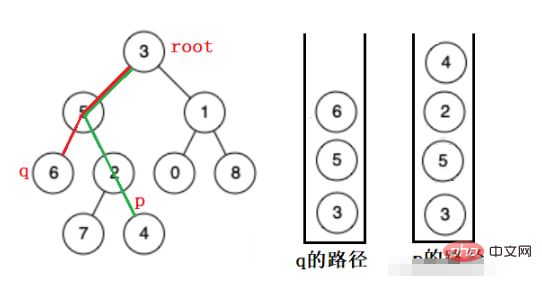
ここではパスを保存するためにスタックが使用されています。ノードがトラバースされると、ノードはスタックに入れられ、ノードの左のツリーと右のツリーが再帰的に検索されます。パスが見つかった場合は、見つからない場合はパスが保持されます。
以下の図で p を探しているとします。
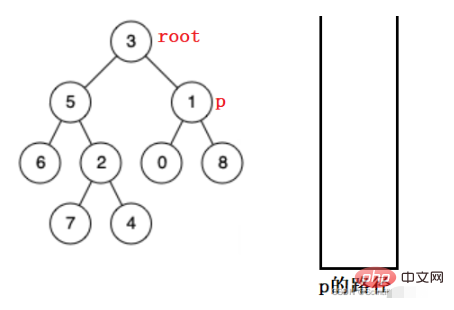 #最初にルート ノードをスタックに入れ、その左側のサブツリーを再帰的に検索します。ルート ノードを見つけて、見つからない場合はポップアップし、右のサブツリーで見つけます。
#最初にルート ノードをスタックに入れ、その左側のサブツリーを再帰的に検索します。ルート ノードを見つけて、見つからない場合はポップアップし、右のサブツリーで見つけます。
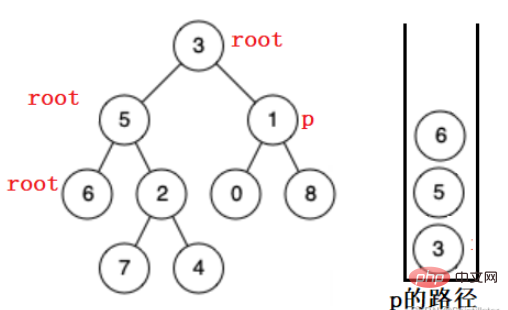 ルートが 6 に達すると、ノードの左側と右側が空であることがわかり、ターゲット ノードがサブツリー内に見つからないことがわかり、6 がポップします。上、右側 5 サブツリー内の検索を続けます。
ルートが 6 に達すると、ノードの左側と右側が空であることがわかり、ターゲット ノードがサブツリー内に見つからないことがわかり、6 がポップします。上、右側 5 サブツリー内の検索を続けます。
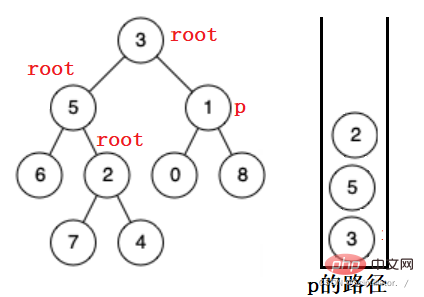 同様に、5 の右のサブツリーでは見つかりません。3 の右のサブツリーに移動して 1 が見つかるまでポップアップします。
同様に、5 の右のサブツリーでは見つかりません。3 の右のサブツリーに移動して 1 が見つかるまでポップアップします。
以上がJava でバイナリ ツリーの最も近い共通の祖先を見つける方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。