
今日の私たちの生活において、グラフの例としては、Twitter、Mastodon などのソーシャル ネットワーク、論文や著者をリンクするあらゆる引用ネットワーク、分子、UML 図などのナレッジ グラフ、百科事典、ハイパーリンクのあるあらゆるものが挙げられます。 、構文ツリーとして表現された文、および 3D グリッドなど、グラフはどこにでもあると言えます。
最近、Hugging Face の研究科学者 Clémentine Fourrier が、「グラフ機械学習の概要」という記事で今日のユビキタス グラフ機械学習を紹介しました。グラフィックスとは何ですか?なぜグラフを使用するのでしょうか?グラフをどのように表現するのが最適でしょうか?人はグラフからどのように学習するのでしょうか? Clémentine Fourrier は、グラフは関係性によってリンクされた項目の記述であると指摘し、その中で、ニューラル以前の手法からグラフ ニューラル ネットワークに至るまで、現在でもグラフ学習手法が一般的に使用されています。
さらに、一部の研究者は最近、Transformer をグラフに適用することを検討し始めています。Transformer は優れたスケーラビリティを備えており、GNN の制限の一部を軽減できるため、その見通しは非常に有望です。
本質的に、グラフは関係にリンクされた項目の説明です。グラフ (またはネットワーク) の項目はノード (または頂点) と呼ばれ、エッジ (またはリンク) によって接続されます。たとえば、ソーシャル ネットワークでは、ノードはユーザー、エッジはユーザー間の接続です。分子では、ノードは原子、エッジは分子結合です。
ご覧のとおり、データを使用するときは、次のことを行う必要があります。まず、同種/異種、有向/無向などを含む最適な表現を検討します。
グラフ レベルでは、主なタスクには以下が含まれます:
ノード層は通常、ノード属性の予測です。たとえば、Alphafold は次のように使用します。ノード属性の予測 分子の全体図における原子の 3D 座標を考慮して、分子が 3D 空間でどのように折りたたまれるかを予測することは、生化学的に難しい問題です。
# エッジ予測には、エッジ属性予測と欠落エッジ予測が含まれます。エッジ属性予測は、一対の薬剤の有害な副作用を考慮して、薬剤の副作用を予測するのに役立ちます。欠落エッジ予測は、グラフ内の 2 つのノードが関連しているかどうかを予測するために推奨システムで使用されます。
サブグラフ レベルでは、コミュニティ検出またはサブグラフ属性の予測を実行できます。ソーシャル ネットワークでは、コミュニティ検出を使用して、人々がどのようにつながっているかを判断できます。サブグラフ属性の予測は、Google マップなどの旅程システムでよく使用され、到着予定時刻を予測するために使用できます。
特定のグラフの進化を予測する場合、トレーニング、検証、テストを含む変換設定のすべてを同じグラフ上で行うことができます。しかし、単一のグラフからトレーニング、評価、またはテストのデータセットを作成するのは簡単ではなく、多くの作業が異なるグラフ (トレーニング/評価/テストの分割) を使用して行われます。これは、誘導設定と呼ばれます。
グラフの処理と操作を表す一般的な方法は 2 つあります。すべてのエッジのセット (すべてのノードのセットによって補完される可能性があります)、またはすべてのエッジのセットとしてのいずれかです。そのノード間の隣接行列。このうち隣接行列とは、どのノードが他のノードと直接接続しているかを示す正方行列(ノードサイズ×ノードサイズ)です。ほとんどのグラフは密に接続されていないため、隣接行列が疎であると計算がより困難になることに注意してください。
グラフは、ML で使用される一般的なオブジェクトとは大きく異なります。グラフのトポロジーは、「シーケンス」(テキストや音声など) や「順序付けられたグリッド」(画像やビデオなど) よりも複雑であるためです。はリストまたは行列として表されますが、この表現は順序付けされたオブジェクトとはみなされません。つまり、文内の単語をスクランブルすると新しい文が作成され、画像をスクランブルしてその列を再配置すると、新しい画像が作成されます。
#注: ハグ フェイス ロゴと中断されたハグ フェイス ロゴはまったく異なる新しい画像です
しかし、これはグラフの場合には当てはまりません。グラフの隣接行列のエッジ リストまたは列をシャッフルしても、同じグラフのままです。
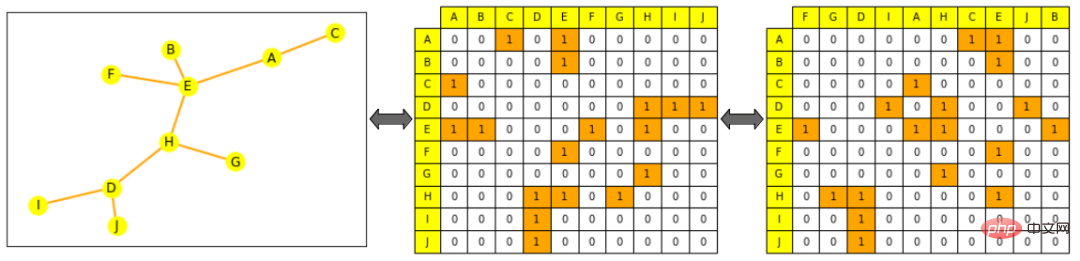
注: 左側は小さな図で、黄色はノード、オレンジ色はエッジを表します。中央の図は隣接行列です。列と行はノードのアルファベット順に配置されています。ノード A の行 (最初の行) が E および C に接続されていることがわかります。右側の図では隣接行列がスクランブルされています (列はアルファベット順ではなくなりました) )、これはまだグラフの有効な表現です。つまり、A はまだ E および C に接続されています。予測子は、ノード、エッジ、または完全なグラフが依存するプロジェクトの意味のある表現を最初に生成することによって、ターゲット タスク用にトレーニングされます。特定のタスクの要件。他のパターンと同様に、オブジェクトの数学的表現を制限して、数学的に同様のオブジェクトに近づけることができます。しかし、この中で、グラフ ML で類似性を厳密に定義することは困難です。たとえば、2 つのノードが同じラベルまたは同じ隣接ノードを持つ場合、そのノードはより類似しますか? #以下に示すように、この記事ではノード表現の生成に焦点を当てています。ノードレベルの表現があれば、エッジまたはグラフレベルの情報を取得できます。エッジ レベルの情報の場合は、ノードのペアを接続するか、点の乗算を行うことができます。グラフ レベルの情報の場合は、すべてのノード レベルで表される連結されたテンソルに対して、平均化や合計などを含むグローバル プーリングを実行できます。ただし、それでも平滑化され、グラフ全体に関する情報が失われます。再帰的な階層コレクションの方が合理的であるか、グラフ内の他のすべてのノードに接続されているダミー ノードを追加して、それをグラフ全体として表すこともできます。
エンジニアリング機能の簡単な使用
ニューラル ネットワークが登場する前は、グラフとその対象項目は、タスク固有の方法で特徴の組み合わせとして表現できました。現在でも、これらの機能はデータ拡張や半教師あり学習で使用されており、より洗練された機能生成方法は存在しますが、タスクに応じてこれらの機能をネットワークに供給する最適な方法を見つけることが重要です。
ノード中心性は、グラフ内のノードの重要性を測定するために使用できます。収束するまで各ノードの隣接中心性を合計するか、ノード間の最短距離の測定によって再帰的に計算されます。再帰的に、ノード次数はそのノードが持つ直接隣接ノードの数です。クラスタリング係数はノード隣接ノードの接続の程度を測定します。グラフレット次数ベクトル計算では、グラフレットが使用できる特定のノードにルートされている異なるグラフレットの数を計算できます。特定の数の接続されたノードを持つすべてのスパークラインを作成します。
#注: 2 ~ 5 ノードの図
エッジ レベルの機能は次のとおりです。これは、2 つのノード間の最短距離、それらの共通の隣接ノード、および 2 つのノード間を移動できる特定の長さのパスを指すカッツ インデックスなど、ノードの接続性に関するより詳細な情報によって補足されます。隣接行列)。
グラフ レベルの特徴には、グラフの類似性と区別性に関する高レベルの情報が含まれています。サブグラフの数は、計算コストは高くなりますが、サブグラフの形状に関する情報を提供します。コアメソッドは、さまざまな「バッグオブノード」メソッド (バッグオブワードと同様) を通じてグラフ間の類似性を測定します。
歩行ベースの方法では、ランダム ウォークでノード i からノード j を訪問する確率を使用して、類似性測定。これらの方法は、ローカル情報とグローバル情報を組み合わせます。たとえば、以前は Node2Vec はグラフ ノード間のランダム ウォークをシミュレートし、文章内の単語を処理して埋め込みを計算するのと同じように、スキップ グラムを使用してこれらのウォークを処理しました。
これらのメソッドは、PageRank メソッドの計算を高速化するためにも使用できます。このメソッドは、評価するためのランダム ウォーキングなどによって、他のノードとの接続に基づいて各ノードに重要度スコアを割り当てます。アクセス頻度。しかし、上記の方法には、新しいノードの埋め込みが取得できない、ノード間の構造の類似性をうまく捉えることができない、追加された機能を使用できないなどの制限があります。
ニューラル ネットワークは、目に見えないデータに一般化できます。前述の表現上の制約を考慮すると、優れたニューラル ネットワークはグラフをどのように処理すべきでしょうか?
2 つのメソッドを以下に示します:
式: P(f(G))=f(P(G))P(f(G))=f(P(G))ここで、f はネットワーク、P は置換関数、G はグラフ
#説明: ノードをネットワークに渡す前にノードを置換することは、以下と同等である必要があります。表現の並べ替え
RNN や CNN など、一般的なニューラル ネットワークは並べ替え不変ではないため、新しいアーキテクチャであるグラフ ニューラル ネットワークが導入されました (元々は状態ベースのマシン)。
#GNN は連続した層で構成されます。 GNN 層は、その近隣ノードと前の層 (メッセージ パッシング) からの自身の表現の組み合わせとしてノードを表します。多くの場合、非線形性を追加するためにアクティベーションが追加されます。他のモデルと比較すると、CNN は固定近傍サイズ (スライディング ウィンドウによる) と順序付け (非順列等分散) を備えた GNN とみなすことができますが、位置埋め込みのない Transformer は完全に接続された入力グラフ上の GNN とみなすことができます。
隣接ノードからの情報を集約するには、合計、平均、および同様の集約方法など、さまざまな方法があります。クラス メソッドには次のものが含まれます:
新しい層ごとに、ノード表現にはますます多くのノードが含まれます。ノードは、直接隣接するノードの集合体である最初の層を通過します。 2 番目の層を通しても、それは依然としてその直接の隣接要素の集合体ですが、その表現には (最初の層からの) 自身の隣接要素も含まれます。 n レベルの後、すべてのノードの表現は、距離 n のすべての隣接ノードのセットになり、その直径が n 未満の場合はグラフ全体の集合になります。 ネットワーク層が多すぎる場合、各ノードが完全なグラフの集合体になる (そしてノード表現がすべてのノードで同じ表現に収束する) というリスクがあります。平滑化の問題は、次の方法で解決できます。 過剰平滑化問題は、Transformer と同様に GNN のスケーリングを妨げるため、グラフ ML の重要な研究領域です。他のモデルでも実証されています。 位置コーディング層を持たないTransformerは順列不変であり、スケーラビリティも優れているため、最近研究が検討され始めています。トランスフォーマーをグラフに適用します。ほとんどの手法は、最適な特徴とグラフを表現する最適な方法を見つけて、この新しいデータに適応するように注意を変えることに重点を置いています。 # 以下に、スタンフォード大学の Open Graph Benchmark で最先端の結果、またはそれに近い結果を達成するいくつかのメソッドを示します。
##さらに、研究「一般的で強力でスケーラブルなグラフ トランスフォーマーのレシピ」では、他の方法とは異なり、モデルではなく、メッセージ パッシング ネットワークを Linear と組み合わせることができる GraphGPS と呼ばれるフレームワークを紹介しています。 (リモート) トランスを組み合わせてハイブリッド ネットワークを簡単に構築できます。このフレームワークには、位置および構造エンコーディング (ノード、グラフ、エッジ レベル)、特徴拡張、ランダム ウォークなどを計算するためのいくつかのツールも含まれています。 論文アドレス: https://arxiv.org/abs/2205.12454 トランスフォーマー グラフの使用はまだ初期段階にありますが、今のところ非常に有望です。より大きなグラフやより密なグラフへのスケーリング、過度の平滑化なしなど、GNN の制限の一部を軽減できます。場合によってはモデル サイズを増やします。 GNN 形状と過度の平滑化の問題
Graph Transformers
# # Graph-to-Sequence Learning 用の Graph Transformer では、埋め込みと位置埋め込みの連結としてノードを表すグラフ Transformer が導入されています。ノードの関係は 2 つの間の最短パスを表し、2 つを 1 つの関係に結合します。 -集中。
最近の研究「Pure Transformers are Powerful Graph Learners」では、メソッドに TokenGT が導入され、入力グラフを一連のノードとエッジの埋め込みとして表現します。つまり、通常の拡張エンベディングを使用します。交差ノード識別子とトレーニング可能なタイプ識別子を使用し、位置埋め込みを行わず、このシーケンスを Transformer への入力として提供するこの方法は、非常にシンプルであると同時に非常に効果的です。 

以上がグラフ機械学習はどこにでもあり、Transformer を使用して GNN の制限を緩和しますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。