Java でグラフ トラバーサルを実装する方法

1. グラフのトラバーサル

グラフ内の特定の頂点から開始して、グラフ内の残りの頂点を訪問します。各頂点は 1 回だけ訪問されます

深さには 2 種類あります。グラフ トラバーサル DFS の最初のトラバーサル、幅優先トラバーサル BFS

2. 深さ優先トラバーサル

深さ優先トラバーサルは、深さを優先してトラバースします。これは、単純に毎回最後に行くことを意味します。バイナリ ツリーの事前順序走査と同様です。

アイデア:

#1. 特定の頂点から開始して深さ優先の走査を実行し、その頂点を訪問済みとしてマークします

2. 頂点を始点として、任意のパスを選択して終点までトラバースし、訪問した頂点にマークを付けます

3. ステップ 2 では、終点までトラバースして前の頂点に戻ります, ステップ 2 を繰り返します

4. すべての頂点の走査の終了

走査の考え方によれば、これは再帰的なプロセスですが、実際、DFS は基本的にバックトラックと同じです。

トラバーサル: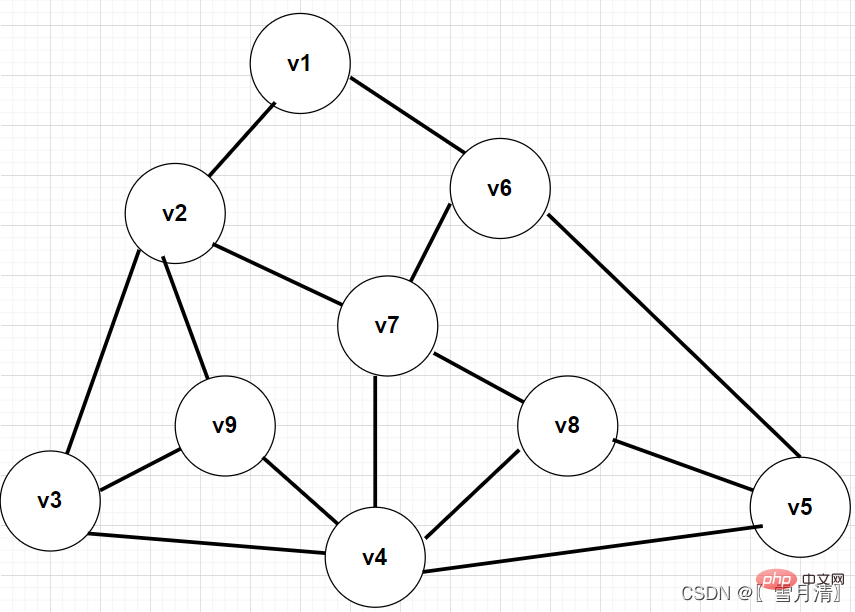

この図を例として、深さ優先トラバーサルを実行します。

	static void dfs(int[][] graph,int idx,boolean[]visit) {
		int len = graph.length;
		//访问过
	 if(visit[idx]) return;
	 //访问该顶点
	 System.out.println("V"+idx);
	 //标志顶点
	 visit[idx] = true;
	 for(int i = 1;i < len;i++) {
	 //访问该顶点相连的所有边
		 if(graph[idx][i] == 1) {
	 //递归进行dfs遍历
		 dfs(graph, i, visit);
		 }
	 }
			
	}

トラバーサル結果:

V1

V2

V3

#V4

V5

V6

V7

V8

V9

グラフを作成するコード:

public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		//顶点数 以1开始
		int n = scanner.nextInt();
		int[][] graph = new int[n+1][n+1];
		//边数
		int m = scanner.nextInt();
		
		for(int i = 1;i <= m;i++) {
			int v1 = scanner.nextInt();
			int v2 = scanner.nextInt();
			graph[v1][v2] = 1;
			graph[v2][v1] = 1;
		}
		
		//标记数组 false表示未访问过 
		boolean[] visit = new boolean[n+1];
		dfs(graph, 1, visit);
		
	}

3. DFS を使用して、有向グラフに循環があるかどうかを判断します

アイデア: 特定の A 頂点をトラバースします。前の頂点に加えて、訪問済みの他の接続された頂点がある場合、サイクルが存在する必要があります

	//默认无环
   static boolean flag = false;
	public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		//顶点数 以1开始
		int n = scanner.nextInt();
		int[][] graph = new int[n+1][n+1];
		//边数
		int m = scanner.nextInt();
		
		for(int i = 1;i <= m;i++) {
			int v1 = scanner.nextInt();
			int v2 = scanner.nextInt();
			graph[v1][v2] = 1;
			
		}
	 //标记数组 true为访问过
		boolean[] visit = new boolean[n+1];
		dfs(graph, 1, visit,1);
		if(flag) 
			System.out.println("有环");
		
	}
	
	static void dfs(int[][] graph,int idx,boolean[]visit,int parent) {
		int len = graph.length;
	
	 System.out.println("V"+idx);
	 //标记顶点
	 visit[idx] = true;
	 for(int i = 1;i < len;i++) {
		 //访问该顶点相连的所有边
		 if(graph[idx][i] == 1) {
		 if( !visit[i] ) {
		 dfs(graph, i, visit,idx);
		 }
		 else if(idx != i) {
			 flag = true;
		 }
		 }
	 }
	
	 
	}

注:は、循環があるかどうかを判断する有向グラフであり、循環があるかどうかを判断する無向グラフです。既存の 2 つのパスの頂点が循環である可能性があるため、循環があるかどうかは無意味です。 #4. 幅優先トラバーサル

幅優先トラバーサルは、幅 (幅) を優先トラバースとして実行されます。バイナリ ツリーのレベル順トラバースと同様です。

アイデア:

1. 幅優先トラバースの開始点として特定の頂点を取得し、その頂点を訪問済みとしてマークします

2.頂点に接続されているがまだ訪問されていないすべての頂点を訪問し、訪問した頂点にマークを付けます

#3.ステップ 2 で訪問した頂点から始めてステップ 1 と 2 を繰り返します

4.すべての頂点の終点をトラバースする

トラバーサルはキューによって支援され、キューのキューイング順序は幅優先のトラバーサル結果です

トラバーサル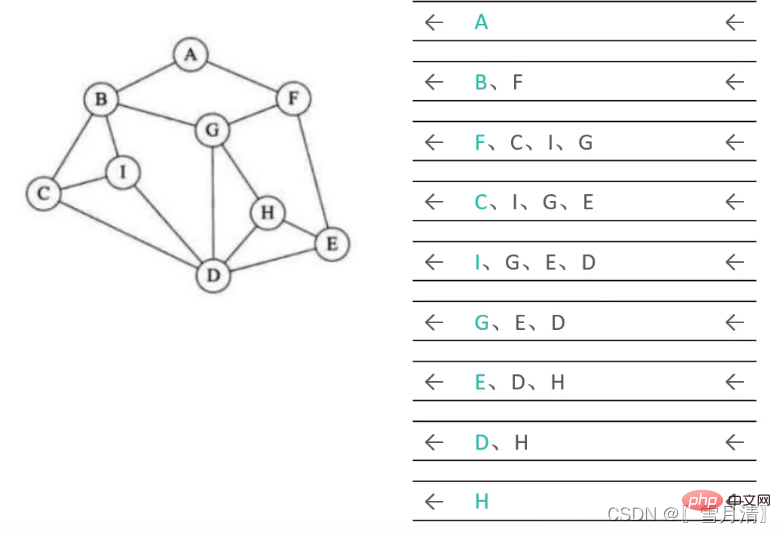

この図を例として、隣接行列法を使用してグラフを作成し、BFS トラバーサルを実行します。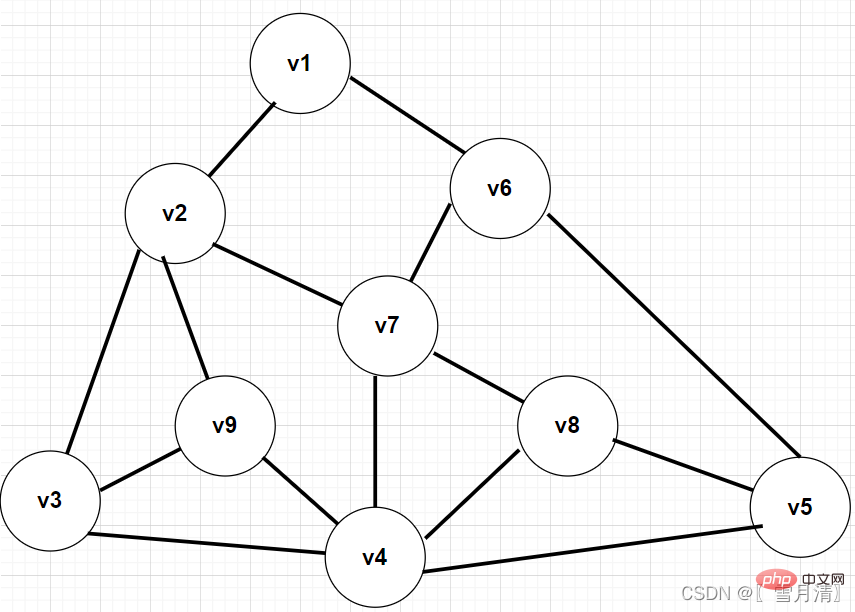

	static void bfs(int[][] graph) {		
		int len = graph.length;
		//标记数组 false表示未访问过 
		boolean[] visit = new boolean[len];
		//辅助队列
		Queue<Integer> queue = new LinkedList<>();
		
		queue.offer(1);
		visit[1] = true;
		
		while(!queue.isEmpty()) {
			int num = queue.poll();
			System.out.println("V"+num);
					
			//遍历该顶点所有相连顶点
			for(int i = 1;i < len;i++) {
				//相连并且没有被访问过
				if(graph[num][i] == 1 && !visit[i]) {
					queue.offer(i);
					visit[i] = true;				
				}
			}
		}	
	}

トラバーサル結果:

V1

V2

V6

V3

V7

V9

V5

V4

V8

グラフを作成するコード

public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		//顶点数 以1开始
		int n = scanner.nextInt();
		int[][] graph = new int[n+1][n+1];
		//边数
		int m = scanner.nextInt();
		
		for(int i = 1;i <= m;i++) {
			int v1 = scanner.nextInt();
			int v2 = scanner.nextInt();
			graph[v1][v2] = 1;
			graph[v2][v1] = 1;
		}
		bfs(graph);
	}

以上がJava でグラフ トラバーサルを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。