時系列予測のための5つのディープラーニングモデルの比較まとめ
マクリダキス M コンペティション シリーズ (それぞれ M4 と M5 と呼ばれます) は、それぞれ 2018 年と 2020 年に開催されました (今年は M6 も開催されました)。知らない人のために説明すると、m シリーズは時系列エコシステムの現在の状態を要約したものであり、現在の理論と予測の実践に経験的かつ客観的な証拠を提供すると考えることができます。
2018 M4 の結果は、純粋な「ML」手法が従来の統計手法を当時予想外だった大幅なパフォーマンスで上回ることを示しました。 2 年後の M5[1] では、最高スコアは「ML」メソッドのみを使用したものでした。そして、上位 50 はすべて基本的に ML ベース (ほとんどがツリー モデル) です。このコンテストでは、LightGBM (時系列予測用) のほか、Amazon の Deepar [2] および N-Beats [3] がデビューしました。 N-Beats モデルは 2020 年にリリースされ、M4 コンペティションの優勝者よりも 3% 優れています。
最近の人工呼吸器圧力予測コンテストでは、ディープラーニング手法を使用してリアルタイム時系列の課題に取り組むことの重要性が実証されました。コンテストの目的は、機械的な肺内の圧力の時間的順序を予測することです。各トレーニング インスタンスは独自の時系列であるため、タスクは複数の時系列の問題になります。優勝チームは、LSTM ネットワークと Transformer ブロックを含む多層ディープ アーキテクチャを提出しました。
過去数年で、MQRNN や DSSM など、多くの有名なアーキテクチャがリリースされました。これらすべてのモデルは、深層学習を使用した時系列予測の分野に多くの新しいことに貢献します。 Kaggle コンテストでの優勝に加えて、次のようなさらなる進歩ももたらしました:
- 多用途性: さまざまなタスクにモデルを使用できる機能。
- MLOP: 実稼働環境でモデルを使用する機能。
- 解釈可能性と解釈可能性: ブラックボックスモデルはそれほど人気がありません。
この記事では、時系列予測に特化した 5 つのディープ ラーニング アーキテクチャについて説明します。論文は次のとおりです:
- N-BEATS(ElementAI)
- DeepAR ( Amazon)
- Spacetimeformer[4]
- Temporal Fusion Transformer または TFT(Google) [5]
- TSFormer (時系列の MAE)[7]
N-BEATS
このモデルは、Yoshua Bengio が共同設立した (残念なことに) 短命に終わった ElementAI 社から直接提供されたものです。トップレベルのアーキテクチャとその主要コンポーネントを図 1 に示します。
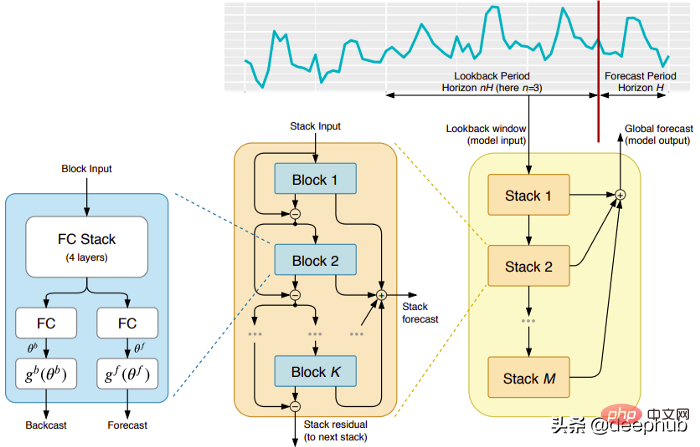
N-BEATS は、フィードフォワード ネットワークのディープ スタックの統合に基づく純粋なディープ ラーニング アーキテクチャです。これは、順方向および逆方向の相互接続によっても行われます。
各ブロックは、前のバックキャストによって生成された残差誤差のみをモデル化し、この誤差に基づいて予測を更新します。このプロセスは、ARIMA モデルをフィッティングする際の Box-Jenkins 法をシミュレートします。
このモデルの主な利点は次のとおりです:
表現力と使いやすさ: モデルは理解しやすく、モジュール構造を持ち、最小限の時系列特徴エンジニアリングを必要とするように設計されています。入力をスケーリングする必要はありません。
モデルには、複数の時系列にわたって一般化する機能があります。つまり、分布がわずかに異なる異なる時系列を入力として使用できます。 N-BEATSではメタ学習によって実現されています。メタ学習プロセスには、内部学習プロセスと外部学習プロセスの 2 つのプロセスが含まれます。内部学習プロセスはブロック内で発生し、モデルが局所的な時間的特徴を捕捉するのに役立ちます。外部学習プロセスはレイヤーを積み重ねて発生し、モデルがすべての時系列のグローバルな特徴を学習するのに役立ちます。
二重残差スタッキング: 残差接続とスタッキングのアイデアは非常に巧妙で、ほぼすべての種類のディープ ニューラル ネットワークで使用されています。同じ原理が N-BEATS の実装にも適用されますが、いくつかの追加の変更が加えられています。各ブロックには 2 つの残差ブランチがあり、1 つはルックバック ウィンドウ (バックキャストと呼ばれます) で実行され、もう 1 つは予測ウィンドウ (予測と呼ばれます) で実行されます。
連続する各ブロックは、前のブロックの再構築されたバックキャストから得られる残差のみをモデル化し、その誤差に基づいて予測を更新します。これは、モデルが有用なバックキャスト信号をより適切に近似するのに役立ち、最終的なスタック予測予測はすべての部分予測の階層的な合計としてモデル化されます。 ARIMA モデルの Box-Jenkins 法をシミュレートするのはこのプロセスです。
解釈可能性: モデルには、一般的なモデルと解釈可能なモデルの 2 つのバリエーションがあります。一般的な変形では、ネットワークは各ブロックの完全に接続された層の最終的な重みを任意に学習します。解釈可能な変形では、各ブロックの最後の層が削除されます。次に、バックキャスト ブランチと予測ブランチに、傾向 (単調関数) と季節性 (周期的周期関数) をシミュレートする特定の行列が乗算されます。
注: 元の N-BEATS 実装は、単変量時系列でのみ機能します。
DeepAR
ディープ ラーニングと自己回帰機能を組み合わせた新しい時系列モデル。図 2 は、DeepAR のトップレベルのアーキテクチャを示しています:
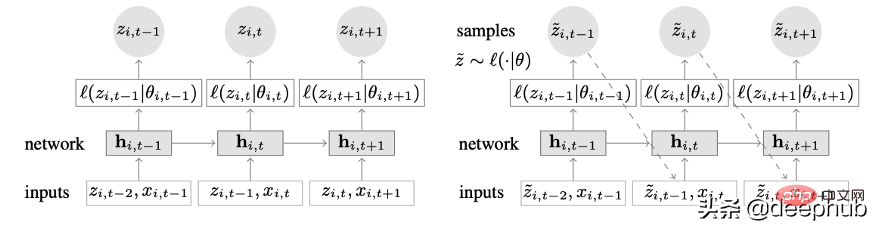
このモデルの主な利点は次のとおりです:
DeepAR は、分布がわずかに異なる複数の時系列を使用することにより、複数の時系列で非常にうまく機能します。 。多くの現実のシナリオにも適用できます。たとえば、電力会社は、それぞれ異なる消費パターン (異なる分布を意味します) を持つ顧客ごとに電力予測サービスを開始したいと考えている場合があります。
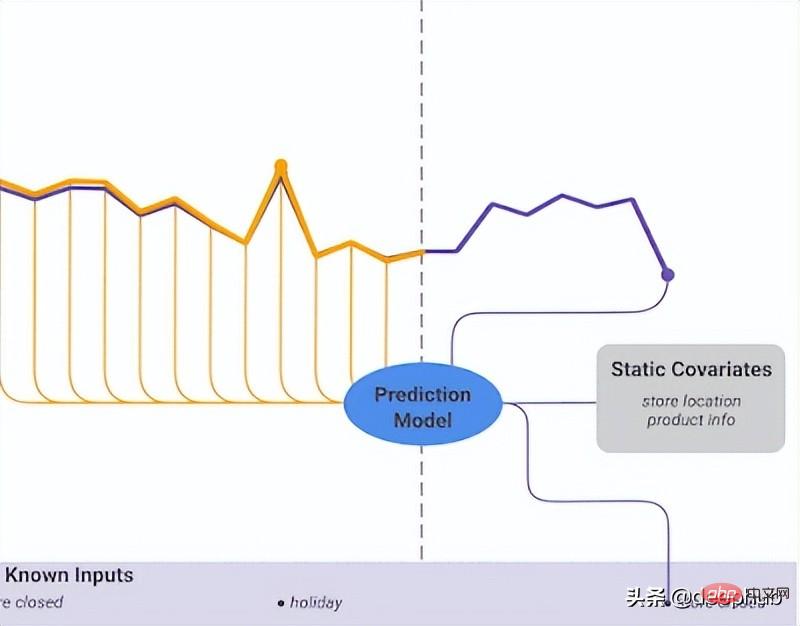
過去のデータに加えて、DeepAR では既知の将来の時系列 (自己回帰モデルの特性) や追加の静的属性も使用できます。前述の電力需要予測シナリオでは、追加の時間変数として月 (値が 1 ~ 12 の整数) を指定できます。各顧客が電力消費量を測定するセンサーに関連付けられていると仮定すると、追加の静的変数は sensor_id や customer_id のようなものになります。
MLP や RNN などのニューラル ネットワーク アーキテクチャを時系列予測に使用することに慣れている場合、重要な前処理手順は、正規化または正規化手法を使用して時系列をスケーリングすることです。これには、DeepAR での手動操作は必要ありません。これは、基礎となるモデルが各時系列 i の自己回帰入力 z を、その時系列の平均であるスケーリング係数 v_i によってスケーリングするためです。具体的には、ペーパー ベンチマークで使用されるスケール ファクターの式は次のとおりです。

#しかし実際には、ターゲット時系列のサイズが大きく異なる場合、前処理中にやはり独自のスケーリングを適用する必要があります。たとえば、エネルギー需要予測シナリオでは、データ セットには、中圧の電力顧客 (メガワット単位で電力を消費する小規模工場など) と低圧電力の顧客 (キロワット単位で電力を消費する家庭など) が含まれる場合があります。
DeepAR は、将来の値を直接出力するのではなく、確率を予測します。これはモンテカルロサンプルとして行われます。これらの予測は、分位損失関数を使用して分位予測を計算するために使用されます。このタイプの損失に慣れていない人のために説明すると、分位損失は推定値だけでなく、その値の周囲の予測区間を計算するためにも使用されます。
時空形成者
時間依存性は、単変量時系列において最も重要です。しかし、複数の時系列シナリオでは、物事はそれほど単純ではありません。たとえば、天気予報タスクがあり、5 つの都市の気温を予測したいとします。これらの都市がある国に属していると仮定しましょう。これまで見てきたことを考慮すると、DeepAR を使用して各都市を外部静的共変量としてモデル化できます。
言い換えれば、モデルは時間的関係と空間的関係の両方を考慮します。これが Spacetimeformer の核となるアイデアです。モデルを使用してこれらの都市/場所間の空間的関係を活用し、それによって追加の有用な依存関係を学習します。これは、モデルが時間的関係と空間的関係の両方を考慮するためです。
時空シーケンスの詳細な研究
名前が示すように、このモデルは内部にトランスフォーマーに基づく構造を使用しています。時系列予測にトランスフォーマーベースのモデルを使用する場合、時間認識埋め込みを生成する一般的な手法は、入力を Time2Vec [6] 埋め込み層に渡すことです (NLP タスクの場合、Time2Vec の代わりに位置エンコード ベクトルが使用されます)。この手法は単変量時系列にはうまく機能しますが、多変量時間入力には意味がありません。言語モデリングでは、文内の各単語が埋め込みによって表現され、単語は本質的に語彙の一部であるのに対し、時系列はそれほど単純ではない可能性があります。
多変量時系列では、特定のタイム ステップ t で、入力形式は x_1,t、x2,t、x_m,t になります。ここで、x_i,t は特徴 i の値、m は特徴/シーケンスの総数。入力を Time2Vec レイヤーに渡すと、時間埋め込みベクトルが生成されます。この埋め込みは実際に何を表すのでしょうか? その答えは、入力コレクション全体を単一のエンティティ (トークン) として表すことです。したがって、モデルはタイム ステップ間の時間的ダイナミクスのみを学習しますが、特徴/変数間の空間的関係は見逃します。
Spacetimeformer は、入力を時空シーケンスと呼ばれる大きなベクトルに平坦化することでこの問題を解決します。入力に T タイム ステップに編成された N 個の変数が含まれている場合、結果の時空間シーケンスには (NxT) ラベルが付けられます。以下の図 3 はこれをわかりやすく示しています:
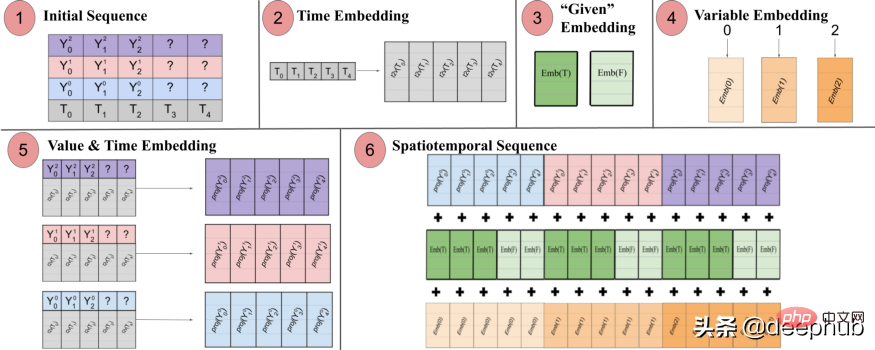
論文には次のように記載されています: 「(1) 時間情報を含む多変量入力フォーマット。デコーダー入力には欠落 (「?」) 値があり、予測時にはゼロに設定されます。 (2) 時系列は、 Time2Vec レイヤー、周期的な入力パターンの代表的な周波数埋め込みを生成 (3) バイナリ埋め込みは、値がコンテキストとして与えられているか、予測する必要があるかを示します (4) 各時系列の整数インデックスを次の「空間」表現にマッピングしますルックアップ テーブルの埋め込み (5) フィードフォワード層を利用して、各時系列の Time2Vec 埋め込みと変数値を投影します (6) 値と時間、変数、および特定の埋め込みの結果を合計することで、MSA をより多くの結果を得ることができます。時間と変数空間の間で一貫性を保ちます。長いシーケンスが入力として取得されます。
言い換えると、最終シーケンスは、時間的、空間的、およびコンテキスト情報を含む統合された埋め込みをエンコードします。しかし、この方法の欠点は、
Temporal Fusion Transformer
Temporal Fusion Transformer (TFT) は、Google がリリースした Transformer ベースの時系列予測モデルです。TFT は、以前のモデルよりも多用途です。
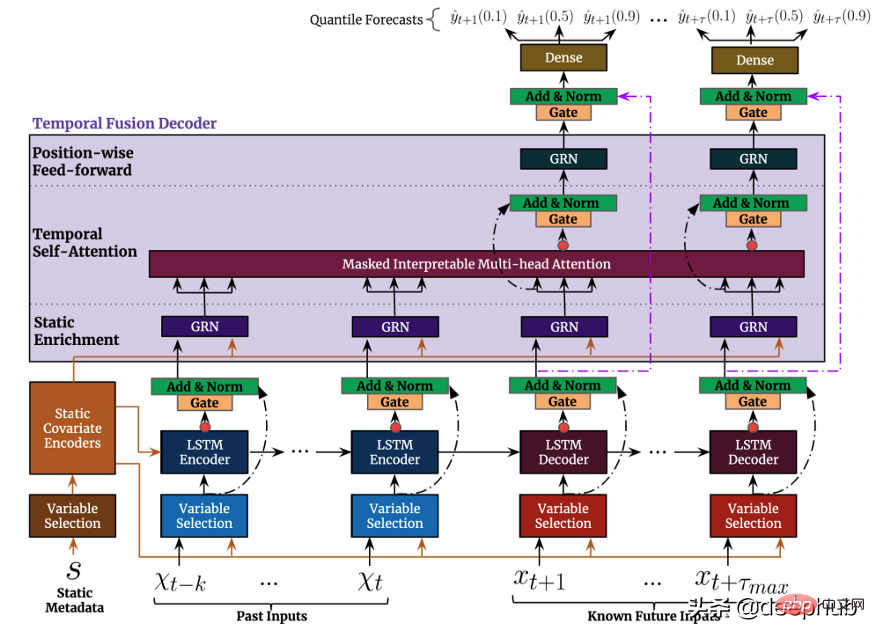
時系列データは自然言語よりも密度が低いデータははるかに少ないです
- NLP データよりも長い時系列データが必要です
- TSFormer の紹介
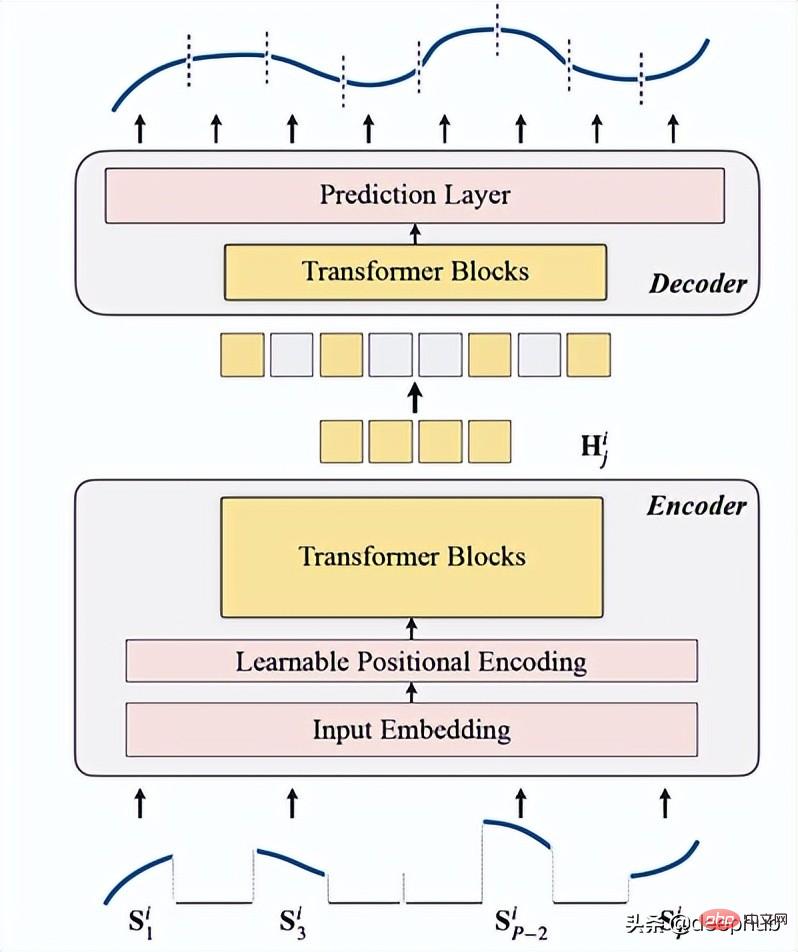
これを次の 4 つのポイントに要約します:
1. マスキング
は、データがエンコーダーに入る前の最初のステップとして使用されます。入力シーケンス (Sᶦ) は、長さが L の P 個のスライスに分散されています。したがって、次のタイム ステップを予測するために使用されるスライディング ウィンドウの長さは P XL です。

オクルージョン率は 75% です (おそらく MAE と同じパラメータを使用しているため、非常に高く見えます)。完了したいのは自己教師ありタスクです。したがって、データが大きくなるほど、エンコーダが少なくなり、計算が速くなります。
これ (入力シーケンス セグメントのマスク) を行う主な理由は、
- セグメント (パッチ) が個々のポイントよりも優れているためです。
- ダウンストリーム モデルの使用が簡単になります (STGNN は入力として単位セグメントを受け取ります)
- エンコーダーの入力サイズを分解できます。
class Patch(nn.Module):<br>def __init__(self, patch_size, input_channel, output_channel, spectral=True):<br>super().__init__()<br>self.output_channel = output_channel<br>self.P = patch_size<br>self.input_channel = input_channel<br>self.output_channel = output_channel<br>self.spectral = spectral<br>if spectral:<br>self.emb_layer = nn.Linear(int(patch_size/2+1)*2, output_channel)<br>else:<br>self.input_embedding = nn.Conv2d(input_channel, output_channel, kernel_size=(self.P, 1), stride=(self.P, 1))<br>def forward(self, input):<br>B, N, C, L = input.shape<br>if self.spectral:<br>spec_feat_ = torch.fft.rfft(input.unfold(-1, self.P, self.P), dim=-1)<br>real = spec_feat_.real<br>imag = spec_feat_.imag<br>spec_feat = torch.cat([real, imag], dim=-1).squeeze(2)<br>output = self.emb_layer(spec_feat).transpose(-1, -2)<br>else:<br>input = input.unsqueeze(-1) # B, N, C, L, 1<br>input = input.reshape(B*N, C, L, 1) # B*N, C, L, 1<br>output = self.input_embedding(input) # B*N, d, L/P, 1<br>output = output.squeeze(-1).view(B, N, self.output_channel, -1)<br>assert output.shape[-1] == L / self.P<br>return output
次はマスキングを生成する関数です:
class MaskGenerator(nn.Module):<br>def __init__(self, mask_size, mask_ratio, distribution='uniform', lm=-1):<br>super().__init__()<br>self.mask_size = mask_size<br>self.mask_ratio = mask_ratio<br>self.sort = True<br>self.average_patch = lm<br>self.distribution = distribution<br>if self.distribution == "geom":<br>assert lm != -1<br>assert distribution in ['geom', 'uniform']<br>def uniform_rand(self):<br>mask = list(range(int(self.mask_size)))<br>random.shuffle(mask)<br>mask_len = int(self.mask_size * self.mask_ratio)<br>self.masked_tokens = mask[:mask_len]<br>self.unmasked_tokens = mask[mask_len:]<br>if self.sort:<br>self.masked_tokens = sorted(self.masked_tokens)<br>self.unmasked_tokens = sorted(self.unmasked_tokens)<br>return self.unmasked_tokens, self.masked_tokens<br>def geometric_rand(self):<br>mask = geom_noise_mask_single(self.mask_size, lm=self.average_patch, masking_ratio=self.mask_ratio) # 1: masked, 0:unmasked<br>self.masked_tokens = np.where(mask)[0].tolist()<br>self.unmasked_tokens = np.where(~mask)[0].tolist()<br># assert len(self.masked_tokens) > len(self.unmasked_tokens)<br>return self.unmasked_tokens, self.masked_tokens<br>def forward(self):<br>if self.distribution == 'geom':<br>self.unmasked_tokens, self.masked_tokens = self.geometric_rand()<br>elif self.distribution == 'uniform':<br>self.unmasked_tokens, self.masked_tokens = self.uniform_rand()<br>else:<br>raise Exception("ERROR")<br>return self.unmasked_tokens, self.masked_tokens2. エンコーディング
入力埋め込み、位置エンコーディング、および Transformer ブロックが含まれます。エンコーダは、マスクされていないパッチに対してのみ実行できます (これも MAE メソッドです)。
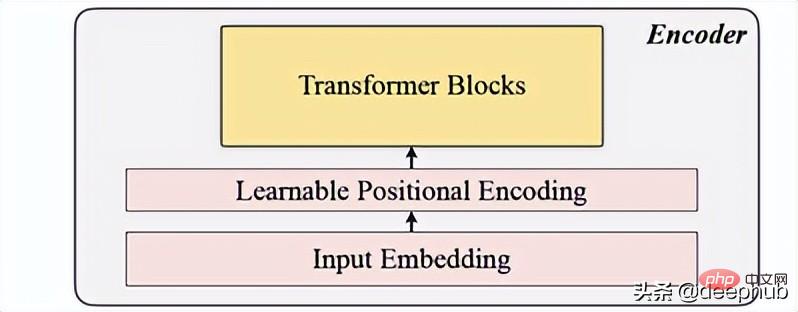
入力埋め込み
線形投影を使用して入力埋め込みを取得します。これにより、マスクされていない空間が潜在空間に変換されます。その式を以下に示します。
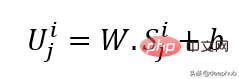
W と B は学習可能なパラメーター、U は次元のモデル入力ベクトルです。
位置エンコーディング
単純な位置エンコーディング層は、新しいシーケンス情報を追加するために使用されます。 「学習可能」という言葉を追加しました。これは、正弦波よりも優れたパフォーマンスを示すのに役立ちます。したがって、学習可能な位置の埋め込みは時系列に対して良好な結果を示します。
class LearnableTemporalPositionalEncoding(nn.Module):<br>def __init__(self, d_model, dropout=0.1, max_len: int = 1000):<br>super().__init__()<br>self.dropout = nn.Dropout(p=dropout)<br>self.pe = nn.Parameter(torch.empty(max_len, d_model), requires_grad=True)<br>nn.init.uniform_(self.pe, -0.02, 0.02)<br><br>def forward(self, X, index):<br>if index is None:<br>pe = self.pe[:X.size(1), :].unsqueeze(0)<br>else:<br>pe = self.pe[index].unsqueeze(0)<br>X = X + pe<br>X = self.dropout(X)<br>return X<br>class PositionalEncoding(nn.Module):<br>def __init__(self, hidden_dim, dropout=0.1):<br>super().__init__()<br>self.tem_pe = LearnableTemporalPositionalEncoding(hidden_dim, dropout)<br>def forward(self, input, index=None, abs_idx=None):<br>B, N, L_P, d = input.shape<br># temporal embedding<br>input = self.tem_pe(input.view(B*N, L_P, d), index=index)<br>input = input.view(B, N, L_P, d)<br># absolute positional embedding<br>return input
Transformer ブロック
この論文では 4 つの Transformer レイヤーを使用していますが、これはコンピューター ビジョンや自然言語処理タスクで一般的であるよりも少ない数です。ここで使用される Transformer は、以下の図 4 に示すように、元の論文で言及されている最も基本的な構造です。
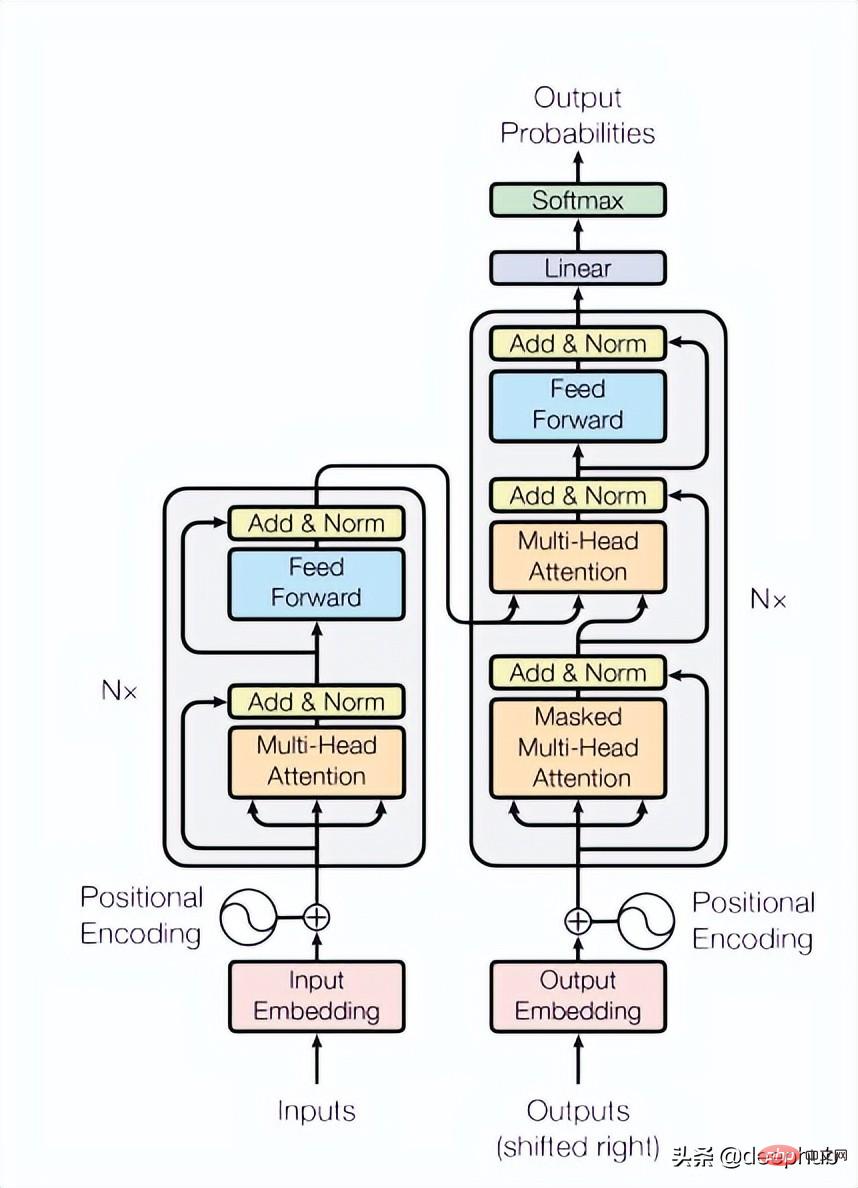
class TransformerLayers(nn.Module):<br>def __init__(self, hidden_dim, nlayers, num_heads=4, dropout=0.1):<br>super().__init__()<br>self.d_model = hidden_dim<br>encoder_layers = TransformerEncoderLayer(hidden_dim, num_heads, hidden_dim*4, dropout)<br>self.transformer_encoder = TransformerEncoder(encoder_layers, nlayers)<br>def forward(self, src):<br>B, N, L, D = src.shape<br>src = src * math.sqrt(self.d_model)<br>src = src.view(B*N, L, D)<br>src = src.transpose(0, 1)<br>output = self.transformer_encoder(src, mask=None)<br>output = output.transpose(0, 1).view(B, N, L, D)<br>return output
3, decoding
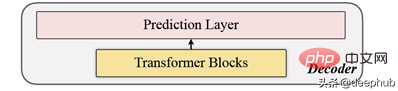
デコーダは一連の Transformer ブロックで構成されます。これはすべてのパッチに適用され (対照的に、MAE のパッチにはすでに位置情報があるため、MAE には位置埋め込みがありません)、レイヤーの数は 1 つだけであり、単純な MLP を使用して、出力の長さを各パッチに等しくします。長さ。
4. 再構成対象

各データ点 (i) のマスキング パッチを計算し、損失関数として mae (平均絶対誤差) を選択します。メインシーケンスと再構築シーケンスの場合。

これは全体的なアーキテクチャです
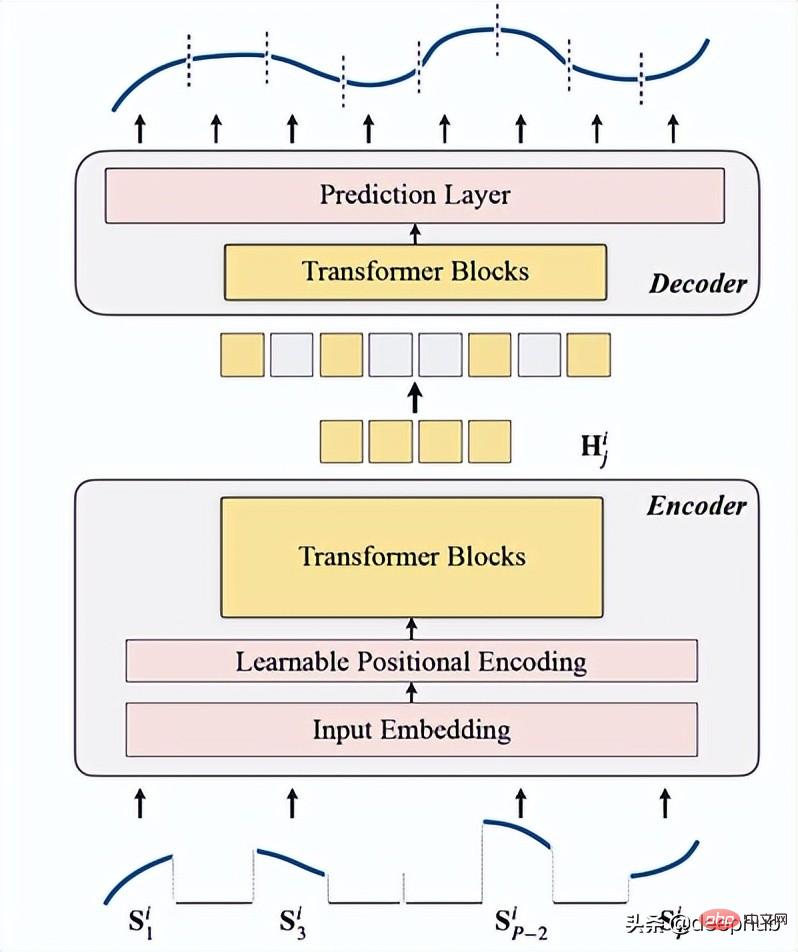
コードの実装は次のとおりです:
def trunc_normal_(tensor, mean=0., std=1.):<br>__call_trunc_normal_(tensor, mean=mean, std=std, a=-std, b=std)<br>def unshuffle(shuffled_tokens):<br>dic = {}<br>for k, v, in enumerate(shuffled_tokens):<br>dic[v] = k<br>unshuffle_index = []<br>for i in range(len(shuffled_tokens)):<br>unshuffle_index.append(dic[i])<br>return unshuffle_index<br>class TSFormer(nn.Module):<br>def __init__(self, patch_size, in_channel, out_channel, dropout, mask_size, mask_ratio, L=6, distribution='uniform', lm=-1, selected_feature=0, mode='Pretrain', spectral=True):<br>super().__init__()<br>self.patch_size = patch_size<br>self.seleted_feature = selected_feature<br>self.mode = mode<br>self.spectral = spectral<br>self.patch = Patch(patch_size, in_channel, out_channel, spectral=spectral)<br>self.pe = PositionalEncoding(out_channel, dropout=dropout)<br>self.mask = MaskGenerator(mask_size, mask_ratio, distribution=distribution, lm=lm)<br>self.encoder = TransformerLayers(out_channel, L)<br>self.decoder = TransformerLayers(out_channel, 1)<br>self.encoder_2_decoder = nn.Linear(out_channel, out_channel)<br>self.mask_token = nn.Parameter(torch.zeros(1, 1, 1, out_channel))<br>trunc_normal_(self.mask_token, std=.02)<br>if self.spectral:<br>self.output_layer = nn.Linear(out_channel, int(patch_size/2+1)*2)<br>else:<br>self.output_layer = nn.Linear(out_channel, patch_size)<br>def _forward_pretrain(self, input):<br>B, N, C, L = input.shape<br># get patches and exec input embedding<br>patches = self.patch(input) <br>patches = patches.transpose(-1, -2) <br># positional embedding<br>patches = self.pe(patches)<br><br># mask tokens<br>unmasked_token_index, masked_token_index = self.mask()<br>encoder_input = patches[:, :, unmasked_token_index, :] <br># encoder<br>H = self.encoder(encoder_input) <br># encoder to decoder<br>H = self.encoder_2_decoder(H)<br># decoder<br># H_unmasked = self.pe(H, index=unmasked_token_index)<br>H_unmasked = H<br>H_masked = self.pe(self.mask_token.expand(B, N, len(masked_token_index), H.shape[-1]), index=masked_token_index)<br>H_full = torch.cat([H_unmasked, H_masked], dim=-2) # # B, N, L/P, d<br>H = self.decoder(H_full)<br># output layer<br>if self.spectral:<br># output = H<br>spec_feat_H_ = self.output_layer(H)<br>real = spec_feat_H_[..., :int(self.patch_size/2+1)]<br>imag = spec_feat_H_[..., int(self.patch_size/2+1):]<br>spec_feat_H = torch.complex(real, imag)<br>out_full = torch.fft.irfft(spec_feat_H)<br>else:<br>out_full = self.output_layer(H)<br># prepare loss<br>B, N, _, _ = out_full.shape <br>out_masked_tokens = out_full[:, :, len(unmasked_token_index):, :]<br>out_masked_tokens = out_masked_tokens.view(B, N, -1).transpose(1, 2)<br>label_full = input.permute(0, 3, 1, 2).unfold(1, self.patch_size, self.patch_size)[:, :, :, self.seleted_feature, :].transpose(1, 2) # B, N, L/P, P<br>label_masked_tokens = label_full[:, :, masked_token_index, :].contiguous()<br>label_masked_tokens = label_masked_tokens.view(B, N, -1).transpose(1, 2)<br># prepare plot<br>## note that the output_full and label_full are not aligned. The out_full in shuffled<br>### therefore, unshuffle for plot<br>unshuffled_index = unshuffle(unmasked_token_index + masked_token_index)<br>out_full_unshuffled = out_full[:, :, unshuffled_index, :]<br>plot_args = {}<br>plot_args['out_full_unshuffled'] = out_full_unshuffled<br>plot_args['label_full'] = label_full<br>plot_args['unmasked_token_index'] = unmasked_token_index<br>plot_args['masked_token_index'] = masked_token_index<br>return out_masked_tokens, label_masked_tokens, plot_args<br>def _forward_backend(self, input):<br>B, N, C, L = input.shape<br># get patches and exec input embedding<br>patches = self.patch(input) <br>patches = patches.transpose(-1, -2) <br># positional embedding<br>patches = self.pe(patches)<br>encoder_input = patches # no mask when running the backend.<br># encoder<br>H = self.encoder(encoder_input) <br>return H<br>def forward(self, input_data):<br><br>if self.mode == 'Pretrain':<br>return self._forward_pretrain(input_data)<br>else:<br>return self._forward_backend(input_data)Afterこの論文では、基本的に MAE、または時系列の MAE を複製することがわかりました。予測段階は MAE と似ています。エンコーダーの出力を特徴として使用し、特徴データを下流のタスクの入力として提供します。興味があります。元の論文を読んで、論文に記載されているコードを確認できます。
以上が時系列予測のための5つのディープラーニングモデルの比較まとめの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7450
7450
 15
15
 1374
1374
 52
52
 77
77
 11
11
 14
14
 7
7
 ORB-SLAM3を超えて! SL-SLAM: 低照度、重度のジッター、弱いテクスチャのシーンはすべて処理されます。
May 30, 2024 am 09:35 AM
ORB-SLAM3を超えて! SL-SLAM: 低照度、重度のジッター、弱いテクスチャのシーンはすべて処理されます。
May 30, 2024 am 09:35 AM
以前に書きましたが、今日は、深層学習テクノロジーが複雑な環境におけるビジョンベースの SLAM (同時ローカリゼーションとマッピング) のパフォーマンスをどのように向上させることができるかについて説明します。ここでは、深部特徴抽出と深度マッチング手法を組み合わせることで、低照度条件、動的照明、テクスチャの弱い領域、激しいセックスなどの困難なシナリオでの適応を改善するように設計された多用途のハイブリッド ビジュアル SLAM システムを紹介します。当社のシステムは、拡張単眼、ステレオ、単眼慣性、ステレオ慣性構成を含む複数のモードをサポートしています。さらに、他の研究にインスピレーションを与えるために、ビジュアル SLAM と深層学習手法を組み合わせる方法も分析します。公開データセットと自己サンプリングデータに関する広範な実験を通じて、測位精度と追跡堅牢性の点で SL-SLAM の優位性を実証しました。
 時系列確率予測のための分位回帰
May 07, 2024 pm 05:04 PM
時系列確率予測のための分位回帰
May 07, 2024 pm 05:04 PM
元のコンテンツの意味を変更したり、コンテンツを微調整したり、コンテンツを書き直したり、継続したりしないでください。 「分位回帰はこのニーズを満たし、定量化された確率で予測間隔を提供します。これは、特に応答変数の条件付き分布が重要な場合に、予測変数と応答変数の間の関係をモデル化するために使用される統計手法です。従来の回帰とは異なります」図 (A): 分位回帰 分位回帰の概念は推定です。一連の回帰子 X と変数の間の線形関係をモデル化する方法です。被説明変数 Y の分位数。既存の回帰モデルは、実際には被説明変数と説明変数の関係を調べる手法です。説明変数と被説明変数の関係に焦点を当てます。
 「Defect Spectrum」は、従来の欠陥検出の限界を打ち破り、超高精度かつ豊富なセマンティックな産業用欠陥検出を初めて実現します。
Jul 26, 2024 pm 05:38 PM
「Defect Spectrum」は、従来の欠陥検出の限界を打ち破り、超高精度かつ豊富なセマンティックな産業用欠陥検出を初めて実現します。
Jul 26, 2024 pm 05:38 PM
現代の製造において、正確な欠陥検出は製品の品質を確保するための鍵であるだけでなく、生産効率を向上させるための核心でもあります。ただし、既存の欠陥検出データセットには、実際のアプリケーションに必要な精度や意味論的な豊富さが欠けていることが多く、その結果、モデルが特定の欠陥カテゴリや位置を識別できなくなります。この問題を解決するために、広州香港科技大学と Simou Technology で構成されるトップの研究チームは、産業欠陥に関する詳細かつ意味的に豊富な大規模なアノテーションを提供する「DefectSpectrum」データセットを革新的に開発しました。表 1 に示すように、他の産業データ セットと比較して、「DefectSpectrum」データ セットは最も多くの欠陥注釈 (5438 個の欠陥サンプル) と最も詳細な欠陥分類 (125 個の欠陥カテゴリ) を提供します。
 NVIDIA 対話モデル ChatQA はバージョン 2.0 に進化し、コンテキストの長さは 128K と記載されています
Jul 26, 2024 am 08:40 AM
NVIDIA 対話モデル ChatQA はバージョン 2.0 に進化し、コンテキストの長さは 128K と記載されています
Jul 26, 2024 am 08:40 AM
オープンな LLM コミュニティは百花繚乱の時代です Llama-3-70B-Instruct、QWen2-72B-Instruct、Nemotron-4-340B-Instruct、Mixtral-8x22BInstruct-v0.1 などがご覧いただけます。優秀なパフォーマーモデル。しかし、GPT-4-Turboに代表される独自の大型モデルと比較すると、オープンモデルには依然として多くの分野で大きなギャップがあります。一般的なモデルに加えて、プログラミングと数学用の DeepSeek-Coder-V2 や視覚言語タスク用の InternVL など、主要な領域に特化したいくつかのオープン モデルが開発されています。
 Google AI が IMO 数学オリンピック銀メダルを獲得、数理推論モデル AlphaProof が発売、強化学習が復活
Jul 26, 2024 pm 02:40 PM
Google AI が IMO 数学オリンピック銀メダルを獲得、数理推論モデル AlphaProof が発売、強化学習が復活
Jul 26, 2024 pm 02:40 PM
AI にとって、数学オリンピックはもはや問題ではありません。木曜日、Google DeepMind の人工知能は、AI を使用して今年の国際数学オリンピック IMO の本当の問題を解決するという偉業を達成し、金メダル獲得まであと一歩のところまで迫りました。先週終了したばかりの IMO コンテストでは、代数、組合せ論、幾何学、数論を含む 6 つの問題が出題されました。 Googleが提案したハイブリッドAIシステムは4問正解で28点を獲得し、銀メダルレベルに達した。今月初め、UCLA 終身教授のテレンス・タオ氏が、100 万ドルの賞金をかけて AI 数学オリンピック (AIMO Progress Award) を宣伝したばかりだったが、予想外なことに、AI の問題解決のレベルは 7 月以前にこのレベルまで向上していた。 IMO に関する質問を同時に行うのが最も難しいのは、最も歴史が長く、規模が最も大きく、最も否定的な IMO です。
 自然の視点: 医療における人工知能のテストは混乱に陥っています。何をすべきでしょうか?
Aug 22, 2024 pm 04:37 PM
自然の視点: 医療における人工知能のテストは混乱に陥っています。何をすべきでしょうか?
Aug 22, 2024 pm 04:37 PM
編集者 | ScienceAI 限られた臨床データに基づいて、何百もの医療アルゴリズムが承認されています。科学者たちは、誰がツールをテストすべきか、そしてどのようにテストするのが最善かについて議論しています。デビン シン氏は、救急治療室で小児患者が治療を長時間待っている間に心停止に陥るのを目撃し、待ち時間を短縮するための AI の応用を模索するようになりました。 SickKids 緊急治療室からのトリアージ データを使用して、Singh 氏らは潜在的な診断を提供し、検査を推奨する一連の AI モデルを構築しました。ある研究では、これらのモデルにより医師の診察が 22.3% 短縮され、医療検査が必要な患者 1 人あたりの結果の処理が 3 時間近く高速化できることが示されました。ただし、研究における人工知能アルゴリズムの成功は、これを証明するだけです。
 結晶相問題を解決するための数百万の結晶データを使用したトレーニング、深層学習手法 PhAI が Science 誌に掲載
Aug 08, 2024 pm 09:22 PM
結晶相問題を解決するための数百万の結晶データを使用したトレーニング、深層学習手法 PhAI が Science 誌に掲載
Aug 08, 2024 pm 09:22 PM
編集者 |KX 今日に至るまで、単純な金属から大きな膜タンパク質に至るまで、結晶学によって決定される構造の詳細と精度は、他のどの方法にも匹敵しません。しかし、最大の課題、いわゆる位相問題は、実験的に決定された振幅から位相情報を取得することのままです。デンマークのコペンハーゲン大学の研究者らは、結晶相の問題を解決するための PhAI と呼ばれる深層学習手法を開発しました。数百万の人工結晶構造とそれに対応する合成回折データを使用して訓練された深層学習ニューラル ネットワークは、正確な電子密度マップを生成できます。この研究では、この深層学習ベースの非経験的構造解法は、従来の非経験的計算法とは異なり、わずか 2 オングストロームの解像度で位相問題を解決できることが示されています。これは、原子解像度で利用可能なデータのわずか 10% ~ 20% に相当します。
 新しい科学的で複雑な質問応答ベンチマークと大規模モデルの評価システムを提供するために、UNSW、アルゴンヌ、シカゴ大学、およびその他の機関が共同で SciQAG フレームワークを立ち上げました。
Jul 25, 2024 am 06:42 AM
新しい科学的で複雑な質問応答ベンチマークと大規模モデルの評価システムを提供するために、UNSW、アルゴンヌ、シカゴ大学、およびその他の機関が共同で SciQAG フレームワークを立ち上げました。
Jul 25, 2024 am 06:42 AM
編集者 |ScienceAI 質問応答 (QA) データセットは、自然言語処理 (NLP) 研究を促進する上で重要な役割を果たします。高品質の QA データ セットは、モデルの微調整に使用できるだけでなく、大規模言語モデル (LLM) の機能、特に科学的知識を理解し推論する能力を効果的に評価することもできます。現在、医学、化学、生物学、その他の分野をカバーする多くの科学 QA データ セットがありますが、これらのデータ セットにはまだいくつかの欠点があります。まず、データ形式は比較的単純で、そのほとんどが多肢選択式の質問であり、評価は簡単ですが、モデルの回答選択範囲が制限され、科学的な質問に回答するモデルの能力を完全にテストすることはできません。対照的に、自由回答型の Q&A




