1. 再帰とは何ですか?
簡単に言えば: 再帰とは、メソッドがそれ自体を呼び出し、呼び出されるたびに異なる変数を渡すことを意味します。再帰は、プログラマが複雑な問題を解決し、コードを簡潔にするのに役立ちます。
実際の応用シナリオ、迷路問題 (バックトラッキング)、再帰 (Recursion) を見てください。
小さなケースを 2 つ挙げます。再帰を理解するのに役立つように、ここでは再帰呼び出しメカニズムのレビューを示します。
public static void test(int n) {
if (n > 2) {
test(n - 1);
}
System.out.println("n=" + n);
}
public static int factorial(int n) {
if (n == 1) {
return 1;
} else {
return factorial(n - 1) * n;
}
}ログイン後にコピー
再帰はどのような問題を解決するために使用されますか?
さまざまな数学的問題: 8 クイーン問題、ハノイの塔、階乗問題など問題、迷路 問題、ボールとバスケットの問題 (Google プログラミング コンテスト)。
再帰は、クイック ソート、マージ ソート、二分探索、分割統治アルゴリズムなどのさまざまなアルゴリズムでも使用されます。
スタックで解決される問題 --> コードは比較的簡潔です。
#再帰に関して従うべき重要なルール- メソッドが実行されると、新しい保護された独立スペース (スタック スペース) が作成されます。
- メソッドのローカル変数は独立しており、n 変数など、互いに影響しません。
- メソッド内で参照型の変数(配列など)を使用した場合、参照型のデータが共有されます。
- 再帰は再帰を終了するための条件に近づく必要があります。そうでない場合は無限再帰になり、StackOverflowError が表示され、死んでしまいます :)。
- メソッドが実行を完了するかリターンに遭遇すると、メソッドは戻ります。メソッドを呼び出した人は誰でも、呼び出した人に結果を返します。同時に、メソッドが実行を完了するかリターンするとき、メソッドも戻り、実行は完了します。
2. コード ケース 1 - 迷路問題
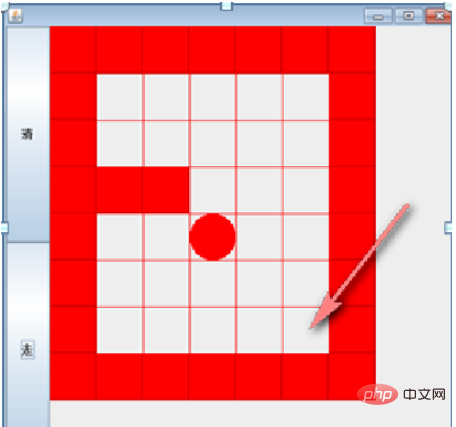
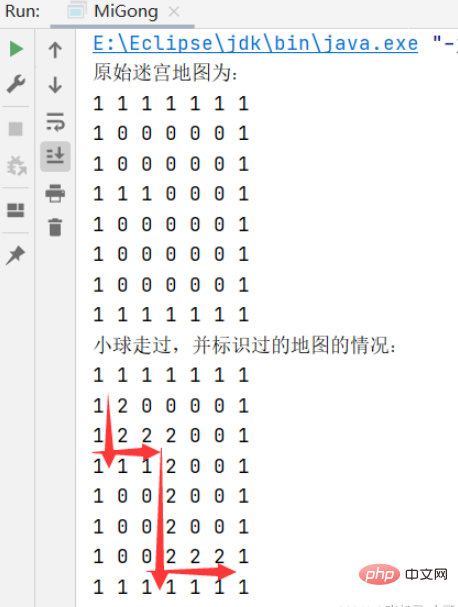
説明: ボールによって取得された経路は、ボールによって設定された経路探索と同じです。プログラマー 戦略には、軌道を見つけるときの上下左右の順序が関係しており、ボールの軌道を取得したら、最初に (右下、左上) を使用し、その後変更することができます。 (右上、左下) に移動して、パスが変更されるかどうかを確認します。バックトラッキング現象をテストします。 package com.szh.recursion;
/**
* 走迷宫问题
*/
public class MiGong {
//使用递归回溯来给小球找路, 说明:
//1. map 表示地图
//2. i,j 表示从地图的哪个位置开始出发 (1,1)
//3. 如果小球能到 map[6][5] 位置，则说明通路找到.
//4. 约定：当 map[i][j] 为 0 表示该点没有走过; 当为 1 表示墙; 2 表示通路可以走;
//5. 在走迷宫时，需要确定一个策略(方法) 下->右->上->左 , 如果该点走不通，再回溯
public static boolean setWay(int[][] map, int i, int j) {
//此时走到了迷宫终点
if (map[6][5] == 2) {
return true;
} else {
if (map[i][j] == 0) { //如果当前这个点还没有走过
//按照策略 下->右->上->左 走
map[i][j] = 2;
if (setWay(map, i + 1, j)) { //下
return true;
} else if (setWay(map, i, j + 1)) { //右
return true;
} else if (setWay(map, i - 1, j)) { //上
return true;
} else { //左
return true;
}
} else { //map[i][j] != 0, 即只能为1、2。 1表示墙（无法走），2表示已经走过了，所以此时直接返回false
return false;
}
}
}
//修改找路的策略，改成 上->右->下->左
public static boolean setWay2(int[][] map, int i, int j) {
if(map[6][5] == 2) { // 通路已经找到ok
return true;
} else {
if(map[i][j] == 0) { //如果当前这个点还没有走过
//按照策略 上->右->下->左
map[i][j] = 2;
if(setWay2(map, i - 1, j)) { //上
return true;
} else if (setWay2(map, i, j + 1)) { //右
return true;
} else if (setWay2(map, i + 1, j)) { //下
return true;
} else { //左
return true;
}
} else {
return false;
}
}
}
public static void main(String[] args) {
//先创建一个二维数组，模拟迷宫 (地图)
int[][] map = new int[8][7];
//使用迷宫中的部分格子表示墙体（置1）
//第一行和最后一行置为1
for (int i = 0; i < 7; i++) {
map[0][i] = 1;
map[7][i] = 1;
}
//第一列和最后一列置为1
for (int i = 0; i < 8; i++) {
map[i][0] = 1;
map[i][6] = 1;
}
//多添加两块墙体
map[3][1] = 1;
map[3][2] = 1;
// map[1][2] = 1;
// map[2][2] = 1;
//输出地图查看
System.out.println("原始迷宫地图为：");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
//使用递归回溯走迷宫
setWay(map, 1, 1);
// setWay2(map, 1, 1);
System.out.println("小球走过，并标识过的地图的情况：");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}
}ログイン後にコピー
3. コード ケース 2 - 8 つのクイーンズ問題
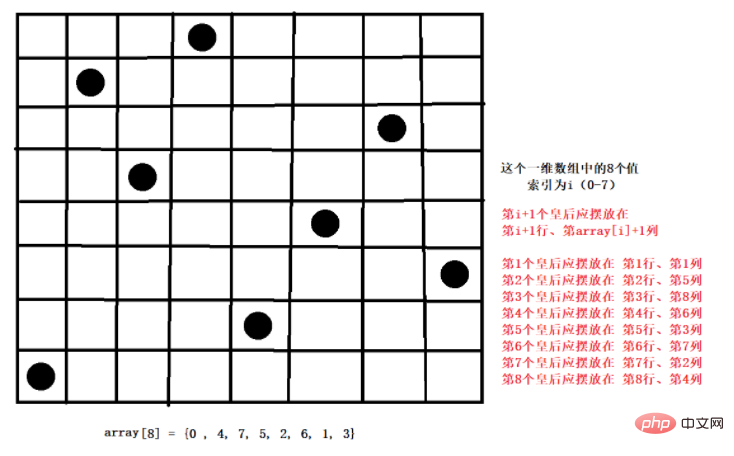
8 つのクイーンズ問題は古くからある有名な問題です。問題は次のとおりです。バックトラッキングアルゴリズムの典型的なケースです。この問題は、1848 年に国際的なチェス プレーヤーのマックス ベセルによって提起されました: 8 つのクイーンを 8 × 8 のグリッドのチェスに配置し、互いに攻撃できないようにする、つまり、2 つのクイーンが同じ位置に配置できないということです。行、列、または対角線?
#最初のクイーンが最初の行、最初の列に配置されます。
2 番目のクイーンを 2 行 1 列目に配置し、OK かどうかを判断します。OK でなければ、引き続き 2 列目と 3 列目に配置し、すべての列を順番に配置します。適切なものを見つけてください。
3 番目のクイーン、または 1 列目、2 列目と続けて、8 番目のクイーンが競合しない位置に配置できるまでは、正解とみなされます。
正しい解が得られると、スタックが前のスタックにロールバックすると、バックトラックが開始されます。つまり、最初のクイーンを最初の列に置き、すべての正しい解を取得します。
次に、戻って最初のクイーンを 2 列目に配置し、ステップ 1、2、3、4 をループで実行し続けます。
package com.szh.recursion;
/**
* 八皇后问题
*/
public class Queue8 {
//定义max表示共有多少个皇后
private int max = 8;
//定义数组，保存皇后放置的位置结果，比如 arr = {0, 4, 7, 5, 2, 6, 1, 3}
int[] array = new int[max];
//共有多少种解法
private static int count = 0;
//共有多少次冲突
private static int judgeCount = 0;
//编写一个方法，放置第n个皇后
//特别注意： check 是 每一次递归时，进入到check中都有 for(int i = 0; i < max; i++)，因此会有回溯
private void check(int n) {
if (n == max) { //n = 8 , 表示这8个皇后已经全部放好了
print();
return;
}
//依次放入皇后，并判断是否冲突
for (int i = 0; i < max; i++) {
//先把当前这个皇后 n , 放到该行的第1列
array[n] = i;
//判断当放置第n个皇后到i列时，是否冲突
if (judge(n)) { // 不冲突
//接着放n+1个皇后,即开始递归
check(n + 1);
}
//如果冲突，就继续执行 array[n] = i; 即将第n个皇后，放置在本行第i列向后的那一列
}
}
//查看当我们放置第n个皇后, 就去检测该皇后是否和前面已经摆放的n-1个皇后冲突
private boolean judge(int n) {
//每摆放一个皇后，就循环去和之前摆好的皇后位置相比较，看是否冲突
for (int i = 0; i < n; i++) {
//1. array[i] == array[n] 表示判断 第n个皇后是否和前面的n-1个皇后在同一列
//2. Math.abs(n-i) == Math.abs(array[n] - array[i]) 表示判断第n个皇后是否和第i皇后是否在同一斜线
//3. 判断是否在同一行, 没有必要，n 表示第几个皇后，这个值每次都在递增，所以必然不在同一行
if (array[i] == array[n] || Math.abs(n - i) == Math.abs(array[n] - array[i])) {
judgeCount++;
return false;
}
}
return true;
}
//打印皇后摆放的具体位置
private void print() {
count++;
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
Queue8 queue8 = new Queue8();
queue8.check(0);
System.out.printf("一共有%d解法\n", count);
System.out.printf("一共判断冲突的次数%d次", judgeCount);
}
}ログイン後にコピー
実際、コードをデバッグするとバックトラックのプロセスが確認できるので、これ以上は言いません。
以上がJava データ構造とアルゴリズムを使用して再帰とバックトラッキングを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
![[Web フロントエンド] Node.js クイック スタート](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
