TSP 問題を解決するために、Python を使用して PSO アルゴリズムを実装するにはどうすればよいですか?
PSO アルゴリズム
始める前に、基本的な PSO アルゴリズムについて説明しましょう。核心は 1 つだけです:

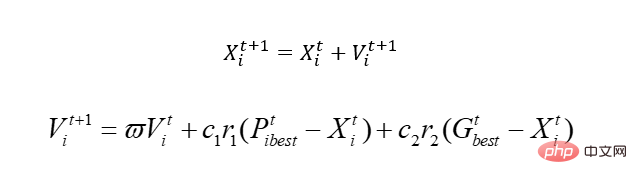
この公式を説明しましょう。そうすれば理解できるでしょう。
古いルールでは、方程式 y=sin(x1) cos(x2)があると仮定します
PSO アルゴリズムは、鳥の渡りをシミュレートすることによって最適化を実現します。さて、この核心について話しましょう。
先ほどの方程式には、x1、x2 という 2 つの変数があります。シミュレートされた鳥なので、ブラインド法を実現するために速度の概念が導入されますが、x は当然のことながら実行可能領域、つまり解空間です。速度を変えることでxが移動、つまりxの値が変化します。このうち、Pbestは鳥が歩いた場所における最適解を表し、Gbestは個体群全体の最適解を表す。どういう意味ですか、つまり、この鳥は移動するにつれて、より悪い位置に移動する可能性があります。なぜなら、遺伝と異なり、悪い場合は殺されてしまうからですが、この鳥は殺されません。もちろん、多くのローカルな問題が関係していますが、ここでは説明しません。完璧なアルゴリズムはありませんが、このアルゴリズムは正しいです。
アルゴリズム プロセス
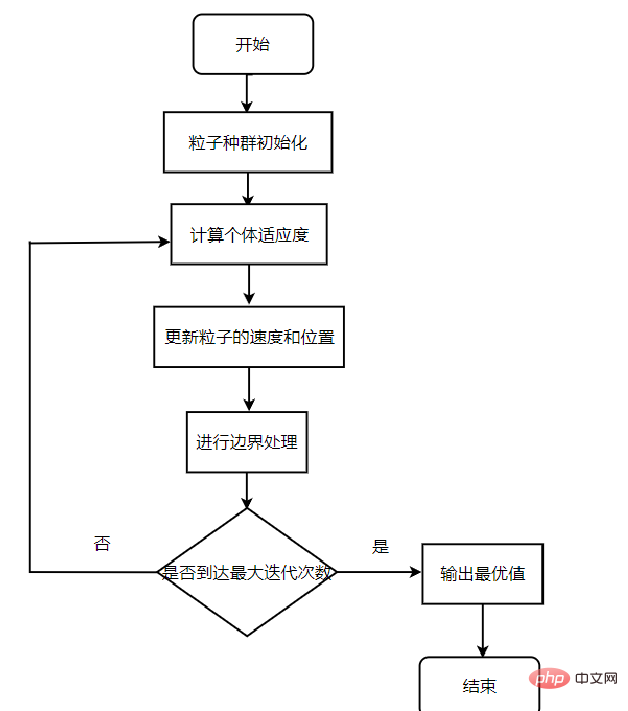
アルゴリズムの主なプロセス:
最初のステップ:粒子群のランダムな位置と速度を初期化し、反復回数を設定します。
ステップ 2: 各粒子のフィットネス値を計算します。
ステップ 3: 各粒子について、その適合度値を私が経験した最適な位置 pbest の適合度値と比較し、より良い場合は、それを現在の個別の最適位置として使用します。
ステップ 4: 各粒子について、その適合度値と gbestg がグローバルに経験した最適な位置の適合度値を比較し、より良い場合は、それを現在のグローバル最適位置として使用します。
ステップ 5: 速度と位置の式に従ってパーティクルの速度と位置を最適化し、パーティクルの位置を更新します。
ステップ 6: 終了条件 (通常は最大サイクル数または最小エラー要件) に達していない場合は、2 番目のステップに戻ります
利点:
PSO アルゴリズムには交差操作や突然変異操作がなく、粒子の速度に依存して探索が完了します。反復進化では、最適な粒子のみが他の粒子に情報を渡すため、探索速度が速くなります。
PSO アルゴリズムにはメモリがあり、粒子グループの過去の最良の位置を記憶し、他の粒子に渡すことができます。
調整が必要なパラメータが少なく、構造がシンプルでエンジニアリングへの実装が容易です。
問題の解によって直接決定される実数エンコードを採用し、問題の解に含まれる変数の数を粒子の次元として直接使用します。
欠点:
速度の動的な調整が欠如しており、局所最適に陥りやすいため、収束精度が低く、収束が困難になります。
離散最適化問題と組み合わせ最適化問題を効果的に解決できません。
パラメータ制御。さまざまな問題に対して、最適な結果を達成するために適切なパラメータを選択する方法。
一部の非デカルト座標系記述問題を効果的に解決できません。
簡単な実装
わかりました。最も単純な実装を見てみましょう:
import numpy as np
import random
class PSO_model:
def __init__(self,w,c1,c2,r1,r2,N,D,M):
self.w = w # 惯性权值
self.c1=c1
self.c2=c2
self.r1=r1
self.r2=r2
self.N=N # 初始化种群数量个数
self.D=D # 搜索空间维度
self.M=M # 迭代的最大次数
self.x=np.zeros((self.N,self.D)) #粒子的初始位置
self.v=np.zeros((self.N,self.D)) #粒子的初始速度
self.pbest=np.zeros((self.N,self.D)) #个体最优值初始化
self.gbest=np.zeros((1,self.D)) #种群最优值
self.p_fit=np.zeros(self.N)
self.fit=1e8 #初始化全局最优适应度
# 目标函数,也是适应度函数(求最小化问题)
def function(self,x):
A = 10
x1=x[0]
x2=x[1]
Z = 2 * A + x1 ** 2 - A * np.cos(2 * np.pi * x1) + x2 ** 2 - A * np.cos(2 * np.pi * x2)
return Z
# 初始化种群
def init_pop(self):
for i in range(self.N):
for j in range(self.D):
self.x[i][j] = random.random()
self.v[i][j] = random.random()
self.pbest[i] = self.x[i] # 初始化个体的最优值
aim=self.function(self.x[i]) # 计算个体的适应度值
self.p_fit[i]=aim # 初始化个体的最优位置
if aim < self.fit: # 对个体适应度进行比较,计算出最优的种群适应度
self.fit = aim
self.gbest = self.x[i]
# 更新粒子的位置与速度
def update(self):
for t in range(self.M): # 在迭代次数M内进行循环
for i in range(self.N): # 对所有种群进行一次循环
aim=self.function(self.x[i]) # 计算一次目标函数的适应度
if aim<self.p_fit[i]: # 比较适应度大小,将小的负值给个体最优
self.p_fit[i]=aim
self.pbest[i]=self.x[i]
if self.p_fit[i]<self.fit: # 如果是个体最优再将和全体最优进行对比
self.gbest=self.x[i]
self.fit = self.p_fit[i]
for i in range(self.N): # 更新粒子的速度和位置
self.v[i]=self.w*self.v[i]+self.c1*self.r1*(self.pbest[i]-self.x[i])+ self.c2*self.r2*(self.gbest-self.x[i])
self.x[i]=self.x[i]+self.v[i]
print("最优值:",self.fit,"位置为:",self.gbest)
if __name__ == '__main__':
# w,c1,c2,r1,r2,N,D,M参数初始化
w=random.random()
c1=c2=2#一般设置为2
r1=0.7
r2=0.5
N=30
D=2
M=200
pso_object=PSO_model(w,c1,c2,r1,r2,N,D,M)#设置初始权值
pso_object.init_pop()
pso_object.update()ソリューション TSP
データ表現
まず第一に、PSO の使用は、実際には以前の遺伝学の使用法と似ています。それでも、母集団を表すために行列を使用し、母集団間の距離を表すために行列を使用します。都市。
# 群体的初始化和路径的初始化
self.population = np.array([0] * self.num_pop * self.num).reshape(
self.num_pop, self.num)
self.fitness = [0] * self.num_pop
"""
计算城市的距离,我们用矩阵表示城市间的距离
"""
self.__matrix_distance = self.__matrix_dis()違い
オリジナルの PSO との最大の違いは何ですか?実際、それは単純で、更新の速度に関係しています。継続的な問題がある場合、実際には次のようになります。
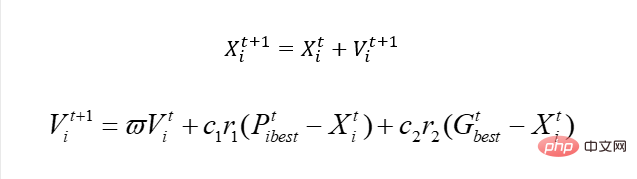
同様に、X を使用して都市番号を表すことはできますが、明らかに、この解決策を使用して都市番号を更新することはできません。スピード。
現時点で速度を更新したい場合は、新しい解決策を使用する必要があるため、この解決策は実際には遺伝的アルゴリズムを使用した X 更新です。端的に言えば、なぜスピードが必要かというと、Xを更新し、Xを良い方向に動かすためです。今は単純に速度アップデートを使用することはできなくなったので、とにかく X を更新するのですが、この X をうまく更新できるソリューションを選択すればよいのではないでしょうか。したがって、ここでは遺伝学を直接使用することができ、速度更新は Pbest と Gbest に基づいて、一定の重みに従って「学習」され、このようにして、この V は Pbest と Gbest の「特性」を持ちます。だとしたら、遺伝的交叉を直接模倣してベストと交配すると、それに対応する「特徴」を学習することはできないのでしょうか?
def cross_1(self, path, best_path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
left, right = min(r1, r2), max(r1, r2)
cross = best_path[left:right + 1]
for i in range(right - left + 1):
for k in range(self.num):
if path[k] == cross[i]:
path[k:self.num - 1] = path[k + 1:self.num]
path[-1] = 0
path[self.num - right + left - 1:self.num] = cross
return path同時に、依然として突然変異が導入される可能性があります。
def mutation(self,path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
path[r1],path[r2] = path[r2],path[r1]
return path完全なコード
わかりました。完全なコードを見てみましょう:
import numpy as np
import matplotlib.pyplot as plt
class HybridPsoTSP(object):
def __init__(self ,data ,num_pop=200):
self.num_pop = num_pop # 群体个数
self.data = data # 城市坐标
self.num =len(data) # 城市个数
# 群体的初始化和路径的初始化
self.population = np.array([0] * self.num_pop * self.num).reshape(
self.num_pop, self.num)
self.fitness = [0] * self.num_pop
"""
计算城市的距离,我们用矩阵表示城市间的距离
"""
self.__matrix_distance = self.__matrix_dis()
def __matrix_dis(self):
"""
计算14个城市的距离,将这些距离用矩阵存起来
:return:
"""
res = np.zeros((self.num, self.num))
for i in range(self.num):
for j in range(i + 1, self.num):
res[i, j] = np.linalg.norm(self.data[i, :] - self.data[j, :])
res[j, i] = res[i, j]
return res
def cross_1(self, path, best_path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
left, right = min(r1, r2), max(r1, r2)
cross = best_path[left:right + 1]
for i in range(right - left + 1):
for k in range(self.num):
if path[k] == cross[i]:
path[k:self.num - 1] = path[k + 1:self.num]
path[-1] = 0
path[self.num - right + left - 1:self.num] = cross
return path
def mutation(self,path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
path[r1],path[r2] = path[r2],path[r1]
return path
def comp_fit(self, one_path):
"""
计算,咱们这个路径的长度,例如A-B-C-D
:param one_path:
:return:
"""
res = 0
for i in range(self.num - 1):
res += self.__matrix_distance[one_path[i], one_path[i + 1]]
res += self.__matrix_distance[one_path[-1], one_path[0]]
return res
def out_path(self, one_path):
"""
输出我们的路径顺序
:param one_path:
:return:
"""
res = str(one_path[0] + 1) + '-->'
for i in range(1, self.num):
res += str(one_path[i] + 1) + '-->'
res += str(one_path[0] + 1) + '\n'
print(res)
def init_population(self):
"""
初始化种群
:return:
"""
rand_ch = np.array(range(self.num))
for i in range(self.num_pop):
np.random.shuffle(rand_ch)
self.population[i, :] = rand_ch
self.fitness[i] = self.comp_fit(rand_ch)
def main(data, max_n=200, num_pop=200):
Path_short = HybridPsoTSP(data, num_pop=num_pop) # 混合粒子群算法类
Path_short.init_population() # 初始化种群
# 初始化路径绘图
fig, ax = plt.subplots()
x = data[:, 0]
y = data[:, 1]
ax.scatter(x, y, linewidths=0.1)
for i, txt in enumerate(range(1, len(data) + 1)):
ax.annotate(txt, (x[i], y[i]))
res0 = Path_short.population[0]
x0 = x[res0]
y0 = y[res0]
for i in range(len(data) - 1):
plt.quiver(x0[i], y0[i], x0[i + 1] - x0[i], y0[i + 1] - y0[i], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.quiver(x0[-1], y0[-1], x0[0] - x0[-1], y0[0] - y0[-1], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.show()
print('初始染色体的路程: ' + str(Path_short.fitness[0]))
# 存储个体极值的路径和距离
best_P_population = Path_short.population.copy()
best_P_fit = Path_short.fitness.copy()
min_index = np.argmin(Path_short.fitness)
# 存储当前种群极值的路径和距离
best_G_population = Path_short.population[min_index, :]
best_G_fit = Path_short.fitness[min_index]
# 存储每一步迭代后的最优路径和距离
best_population = [best_G_population]
best_fit = [best_G_fit]
# 复制当前群体进行交叉变异
x_new = Path_short.population.copy()
for i in range(max_n):
# 更新当前的个体极值
for j in range(num_pop):
if Path_short.fitness[j] < best_P_fit[j]:
best_P_fit[j] = Path_short.fitness[j]
best_P_population[j, :] = Path_short.population[j, :]
# 更新当前种群的群体极值
min_index = np.argmin(Path_short.fitness)
best_G_population = Path_short.population[min_index, :]
best_G_fit = Path_short.fitness[min_index]
# 更新每一步迭代后的全局最优路径和解
if best_G_fit < best_fit[-1]:
best_fit.append(best_G_fit)
best_population.append(best_G_population)
else:
best_fit.append(best_fit[-1])
best_population.append(best_population[-1])
# 将每个个体与个体极值和当前的群体极值进行交叉
for j in range(num_pop):
# 与个体极值交叉
x_new[j, :] = Path_short.cross_1(x_new[j, :], best_P_population[j, :])
fit = Path_short.comp_fit(x_new[j, :])
# 判断是否保留
if fit < Path_short.fitness[j]:
Path_short.population[j, :] = x_new[j, :]
Path_short.fitness[j] = fit
# 与当前极值交叉
x_new[j, :] = Path_short.cross_1(x_new[j, :], best_G_population)
fit = Path_short.comp_fit(x_new[j, :])
if fit < Path_short.fitness[j]:
Path_short.population[j, :] = x_new[j, :]
Path_short.fitness[j] = fit
# 变异
x_new[j, :] = Path_short.mutation(x_new[j, :])
fit = Path_short.comp_fit(x_new[j, :])
if fit <= Path_short.fitness[j]:
Path_short.population[j] = x_new[j, :]
Path_short.fitness[j] = fit
if (i + 1) % 20 == 0:
print('第' + str(i + 1) + '步后的最短的路程: ' + str(Path_short.fitness[min_index]))
print('第' + str(i + 1) + '步后的最优路径:')
Path_short.out_path(Path_short.population[min_index, :]) # 显示每一步的最优路径
Path_short.best_population = best_population
Path_short.best_fit = best_fit
return Path_short # 返回结果类
if __name__ == '__main__':
data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))
main(data)初始染色体的路程: 71.30211569672313
第20步后的最短的路程: 29.340520066994223
第20步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第40步后的最短的路程: 29.340520066994223
第40步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第60步后的最短的路程: 29.340520066994223
第60步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第80步后的最短的路程: 29.340520066994223
第80步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第100步后的最短的路程: 29.340520066994223
第100步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第120步后的最短的路程: 29.340520066994223
第120步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第140步后的最短的路程: 29.340520066994223
第140步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第160步后的最短的路程: 29.340520066994223
第160步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第180步后的最短的路程: 29.340520066994223
第180步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第200步后的最短的路程: 29.340520066994223
第200步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
可以看到收敛速度还是很快的。
特点分析
ok,到目前为止的话,我们介绍了两个算法去解决TSP或者是优化问题。我们来分析一下,这些算法有什么特点,为啥可以达到我们需要的优化效果。其实不管是遗传还是PSO,你其实都可以发现,有一个东西,我们可以暂且叫它环境压力。我们通过物竞天择,或者鸟类迁移,进行模拟寻优。而之所以需要这样做,是因为我们指定了一个规则,在我们的规则之下。我们让模拟的种群有一种压力去靠拢,其中物竞天择和鸟类迁移只是我们的一种手段,去应对这样的“压力”。所以的对于这种算法而言,最核心的点就两个:
设计环境压力
我们需要做优化问题,所以我们必须要能够让我们的解往那个方向走,需要一个驱动,需要一个压力。因此我们需要设计这样的一个环境,在遗传算法,粒子群算法是通过种群当中的生存,来进行设计的它的压力是我们的目标函数。由种群和目标函数(目标指标)构成了一个环境和压力。
设计压力策略
之后的话,我们设计好了一个环境和压力,那么未来应对这种压力,我们需要去设计一种策略,来应付这种压力。遗传算法是通过PUA自己,也就是种群的优胜略汰。PSO是通过学习,学习种群的优秀粒子和过去自己家的优秀“祖先”来应对这种压力的。
强化学习
所以的话,我们是否可以使用别的方案来实现这种优化效果。,在强化学习的算法框架里面的话,我们明确的知道了为什么他们可以实现优化,是环境压力+压力策略。恰好咱们强化学习是有环境的,适应函数和环境恰好可以组成环境+压力。本身的算法收敛过程就是我们的压力策略。所以我们完全是可以直接使用强化学习进行这个处理的。那么在这里咱们就来使用强化学习在下一篇文章当中。
以上がTSP 問題を解決するために、Python を使用して PSO アルゴリズムを実装するにはどうすればよいですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7469
7469
 15
15
 1376
1376
 52
52
 77
77
 11
11
 19
19
 29
29
 mysqlは支払う必要がありますか
Apr 08, 2025 pm 05:36 PM
mysqlは支払う必要がありますか
Apr 08, 2025 pm 05:36 PM
MySQLには、無料のコミュニティバージョンと有料エンタープライズバージョンがあります。コミュニティバージョンは無料で使用および変更できますが、サポートは制限されており、安定性要件が低く、技術的な能力が強いアプリケーションに適しています。 Enterprise Editionは、安定した信頼性の高い高性能データベースを必要とするアプリケーションに対する包括的な商業サポートを提供し、サポートの支払いを喜んでいます。バージョンを選択する際に考慮される要因には、アプリケーションの重要性、予算編成、技術スキルが含まれます。完璧なオプションはなく、最も適切なオプションのみであり、特定の状況に応じて慎重に選択する必要があります。
 インストール後にMySQLの使用方法
Apr 08, 2025 am 11:48 AM
インストール後にMySQLの使用方法
Apr 08, 2025 am 11:48 AM
この記事では、MySQLデータベースの操作を紹介します。まず、MySQLWorkBenchやコマンドラインクライアントなど、MySQLクライアントをインストールする必要があります。 1. mysql-uroot-pコマンドを使用してサーバーに接続し、ルートアカウントパスワードでログインします。 2。CreatedAtaBaseを使用してデータベースを作成し、データベースを選択します。 3. createTableを使用してテーブルを作成し、フィールドとデータ型を定義します。 4. INSERTINTOを使用してデータを挿入し、データをクエリし、更新することでデータを更新し、削除してデータを削除します。これらの手順を習得することによってのみ、一般的な問題に対処することを学び、データベースのパフォーマンスを最適化することでMySQLを効率的に使用できます。
 MySQLダウンロードファイルが破損しており、インストールできません。修復ソリューション
Apr 08, 2025 am 11:21 AM
MySQLダウンロードファイルが破損しており、インストールできません。修復ソリューション
Apr 08, 2025 am 11:21 AM
mysqlダウンロードファイルは破損していますが、どうすればよいですか?残念ながら、MySQLをダウンロードすると、ファイルの破損に遭遇できます。最近は本当に簡単ではありません!この記事では、誰もが迂回を避けることができるように、この問題を解決する方法について説明します。それを読んだ後、損傷したMySQLインストールパッケージを修復するだけでなく、将来の行き詰まりを避けるために、ダウンロードとインストールプロセスをより深く理解することもできます。最初に、ファイルのダウンロードが破損した理由について話しましょう。これには多くの理由があります。ネットワークの問題は犯人です。ダウンロードプロセスの中断とネットワーク内の不安定性は、ファイル腐敗につながる可能性があります。ダウンロードソース自体にも問題があります。サーバーファイル自体が壊れており、もちろんダウンロードすると壊れています。さらに、いくつかのウイルス対策ソフトウェアの過度の「情熱的な」スキャンもファイルの破損を引き起こす可能性があります。診断問題:ファイルが本当に破損しているかどうかを判断します
 MySQLはダウンロード後にインストールできません
Apr 08, 2025 am 11:24 AM
MySQLはダウンロード後にインストールできません
Apr 08, 2025 am 11:24 AM
MySQLのインストール障害の主な理由は次のとおりです。1。許可の問題、管理者として実行するか、SUDOコマンドを使用する必要があります。 2。依存関係が欠落しており、関連する開発パッケージをインストールする必要があります。 3.ポート競合では、ポート3306を占めるプログラムを閉じるか、構成ファイルを変更する必要があります。 4.インストールパッケージが破損しているため、整合性をダウンロードして検証する必要があります。 5.環境変数は誤って構成されており、環境変数はオペレーティングシステムに従って正しく構成する必要があります。これらの問題を解決し、各ステップを慎重に確認して、MySQLを正常にインストールします。
 MySQLインストール後に開始できないサービスのソリューション
Apr 08, 2025 am 11:18 AM
MySQLインストール後に開始できないサービスのソリューション
Apr 08, 2025 am 11:18 AM
MySQLは開始を拒否しましたか?パニックにならないでください、チェックしてみましょう!多くの友人は、MySQLのインストール後にサービスを開始できないことを発見し、彼らはとても不安でした!心配しないでください、この記事はあなたがそれを落ち着いて対処し、その背後にある首謀者を見つけるためにあなたを連れて行きます!それを読んだ後、あなたはこの問題を解決するだけでなく、MySQLサービスの理解と問題のトラブルシューティングのためのあなたのアイデアを改善し、より強力なデータベース管理者になることができます! MySQLサービスは開始に失敗し、単純な構成エラーから複雑なシステムの問題に至るまで、多くの理由があります。最も一般的な側面から始めましょう。基本知識:サービススタートアッププロセスMYSQLサービススタートアップの簡単な説明。簡単に言えば、オペレーティングシステムはMySQL関連のファイルをロードし、MySQLデーモンを起動します。これには構成が含まれます
 高負荷アプリケーションのMySQLパフォーマンスを最適化する方法は?
Apr 08, 2025 pm 06:03 PM
高負荷アプリケーションのMySQLパフォーマンスを最適化する方法は?
Apr 08, 2025 pm 06:03 PM
MySQLデータベースパフォーマンス最適化ガイドリソース集約型アプリケーションでは、MySQLデータベースが重要な役割を果たし、大規模なトランザクションの管理を担当しています。ただし、アプリケーションのスケールが拡大すると、データベースパフォーマンスのボトルネックが制約になることがよくあります。この記事では、一連の効果的なMySQLパフォーマンス最適化戦略を検討して、アプリケーションが高負荷の下で効率的で応答性の高いままであることを保証します。実際のケースを組み合わせて、インデックス作成、クエリ最適化、データベース設計、キャッシュなどの詳細な主要なテクノロジーを説明します。 1.データベースアーキテクチャの設計と最適化されたデータベースアーキテクチャは、MySQLパフォーマンスの最適化の基礎です。いくつかのコア原則は次のとおりです。適切なデータ型を選択し、ニーズを満たす最小のデータ型を選択すると、ストレージスペースを節約するだけでなく、データ処理速度を向上させることもできます。
 MySQLインストール後にデータベースのパフォーマンスを最適化する方法
Apr 08, 2025 am 11:36 AM
MySQLインストール後にデータベースのパフォーマンスを最適化する方法
Apr 08, 2025 am 11:36 AM
MySQLパフォーマンスの最適化は、インストール構成、インデックス作成、クエリの最適化、監視、チューニングの3つの側面から開始する必要があります。 1。インストール後、INNODB_BUFFER_POOL_SIZEパラメーターやclose query_cache_sizeなど、サーバーの構成に従ってmy.cnfファイルを調整する必要があります。 2。過度のインデックスを回避するための適切なインデックスを作成し、説明コマンドを使用して実行計画を分析するなど、クエリステートメントを最適化します。 3. MySQL独自の監視ツール(ShowProcessList、ShowStatus)を使用して、データベースの健康を監視し、定期的にデータベースをバックアップして整理します。これらの手順を継続的に最適化することによってのみ、MySQLデータベースのパフォーマンスを改善できます。
 mysqlはインターネットが必要ですか?
Apr 08, 2025 pm 02:18 PM
mysqlはインターネットが必要ですか?
Apr 08, 2025 pm 02:18 PM
MySQLは、基本的なデータストレージと管理のためにネットワーク接続なしで実行できます。ただし、他のシステムとのやり取り、リモートアクセス、または複製やクラスタリングなどの高度な機能を使用するには、ネットワーク接続が必要です。さらに、セキュリティ対策(ファイアウォールなど)、パフォーマンスの最適化(適切なネットワーク接続を選択)、およびデータバックアップは、インターネットに接続するために重要です。




