Python でモンテカルロシミュレーションを実装する方法と手順-Python チュートリアル-php.cn

Python でモンテカルロシミュレーションを実装する方法と手順

WBOY

リリース： 2023-05-08 11:37:08

転載

3548 人が閲覧しました

Python でモンテカルロシミュレーションを実装する方法と手順

モンテカルロシミュレーションとは

モンテカルロシミュレーションは、ランダムシミュレーションを通じてイベントが発生する確率を計算する、確率統計に基づく手法です。プロジェクト管理では、モンテカルロシミュレーションは主に、プロジェクトの期間やコストなどの主要な指標の確率分布を計算するために使用され、プロジェクトマネージャーがリスクをより適切に管理し、意思決定を行うのに役立ちます。

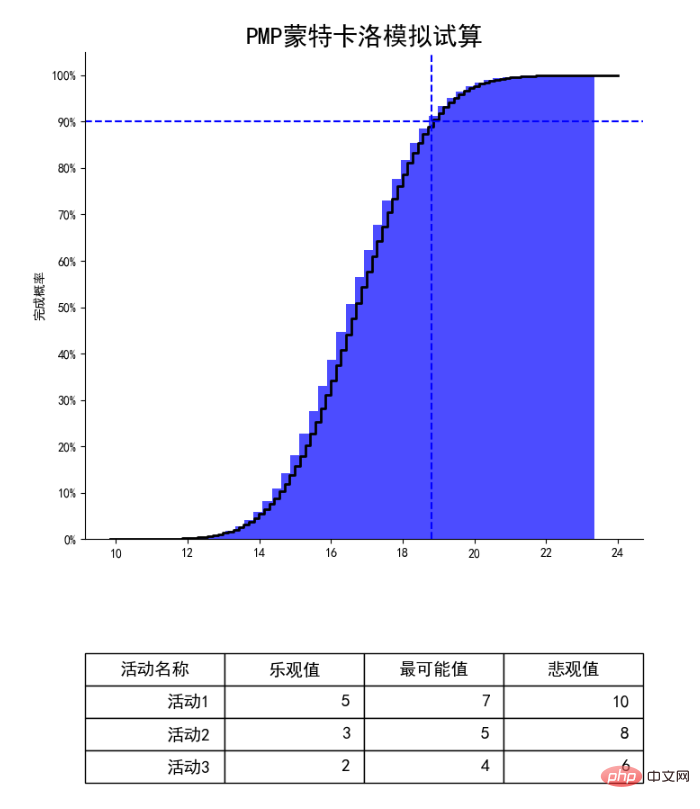
上の図を見てみましょう。この図は、3 つのプロジェクトアクティビティ (アクティビティ 1、アクティビティ 2、およびアクティビティ 3) のモンテカルロシミュレーションです。シミュレーションは、3 つのアクティビティの 3 点推定に基づいています。次に、コンピュータにランダムな予算計算を 1,000,000 回実行するよう依頼し、上の画像が得られました。

上の図の青い点線の交点を例に考えてみましょう。この点は何を指すのでしょうか? Y 軸を見てみましょう。ここでの 90% は、完了の確率が 90% であることを指します。この点に対応する横軸は 19 日に近いです。つまり、コンピュータシミュレーションを100万回繰り返したということです。プロジェクトが 19 日以内に完了する確率は 90% です。

プロジェクトを行った学生は皆、顧客やリーダーが常に私たちに、より速く、より速く、より速く進むことを望んでいることを知っています。リーダーは、19日はなく、16日しかないと言いました。この時、プロジェクトマネージャーとして上記のグラフから、16日間のY軸に対応するX軸の値が約30%であることが分かりました。リーダーに聞いてください「的中率はわずか 30% です。賭けますか?

これは「科学的な占い」の良い方法です。重要なのはシンプルさと、それを裏付ける確率論です。

Python 実装

Python でプロジェクト管理のモンテカルロシミュレーションを計算するにはどうすればよいですか?これは実際には非常に簡単で、Python の numpy ライブラリと matplotlib ライブラリを使用して計算と描画を実行できます。 Tian 先生が完全なコードを以下に示します:

#!/usr/bin/env python
# -*- coding:utf-8 -*-
"""
#-----------------------------------------------------------------------------
#                     --- TDOUYA STUDIOS ---
#-----------------------------------------------------------------------------
#
# @Project : di08-tdd-cdg-python-learning
# @File    : monte_carlo.py
# @Author  : tianxin.xp@gmail.com
# @Date    : 2023/3/12 18:22
#
# 用Python实现蒙特卡洛模拟
#
#--------------------------------------------------------------------------"""
from datetime import datetime

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.ticker import FuncFormatter, MultipleLocator
from scipy.stats import norm

plt.rcParams[&#39;font.sans-serif&#39;] = [&#39;SimHei&#39;]
plt.rcParams[&#39;axes.unicode_minus&#39;] = False


def to_percent(y, position):
    # 将纵轴用百分数表示
    return &#39;{:.0f}%&#39;.format(100 * y)


class Activity:
    """ 活动类，用于表示一个项目中的活动

   Attributes:
       name (str): 活动名称
       optimistic (float): 乐观时间
       pessimistic (float): 悲观时间
       most_likely (float): 最可能时间
   """

    def __init__(self, name, optimistic, pessimistic, most_likely):
        """
            初始化活动类

            Args:
                name (str): 活动名称
                optimistic (float): 乐观时间
                pessimistic (float): 悲观时间
                most_likely (float): 最可能时间
        """
        self.name = name
        self.optimistic = optimistic
        self.pessimistic = pessimistic
        self.most_likely = most_likely


class PMP:
    """
    PMP类用于进行项目管理中的相关计算：
    方法：
    monte_carlo_simulation : 蒙特卡洛模拟试算，包括计算项目工期、平均值、标准差、绘制积累图和概率密度曲线等功能。
    """

    def __init__(self, activities):
        """
        初始化PMP类，传入活动列表。
        :param activities: 活动列表，包括活动名称、乐观值、最可能值和悲观值。
        """
        self.activities = activities

    def monte_carlo_simulation(self, n):
        """
        进行蒙特卡洛模拟试算，计算项目工期、平均值、标准差、绘制积累图和概率密度曲线等。
        :param n: 模拟次数。
        """
        # 模拟参数和变量
        t = []
        for activity in self.activities:
            t.append(np.random.triangular(activity.optimistic, activity.most_likely, activity.pessimistic, n))

        # 计算项目工期
        project_duration = sum(t)

        # 计算平均值和标准差
        mean_duration = np.mean(project_duration)
        std_duration = np.std(project_duration)

        # 绘制积累图
        fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(8, 10), gridspec_kw={&#39;height_ratios&#39;: [3, 1]})

        ax1.hist(project_duration, bins=50, density=True, alpha=0.7, color=&#39;blue&#39;, cumulative=True)
        ax1.yaxis.set_major_locator(MultipleLocator(0.1))
        ax1.yaxis.set_major_formatter(FuncFormatter(to_percent))
        ax1.set_ylabel(&#39;完成概率&#39;)
        ax1.set_title(&#39;PMP蒙特卡洛模拟试算&#39;, fontsize=20)

        # 绘制概率密度曲线
        xmin, xmax = ax1.get_xlim()
        x = np.linspace(xmin, xmax, 100)
        p = norm.cdf(x, mean_duration, std_duration)
        ax1.plot(x, p, &#39;k&#39;, linewidth=2, drawstyle=&#39;steps-post&#39;)

        # 找到完成概率90%的点
        x_90 = norm.ppf(0.9, mean_duration, std_duration)

        # 绘制垂线
        ax1.axvline(x_90, linestyle=&#39;--&#39;, color=&#39;blue&#39;)
        ax1.axhline(0.9, linestyle=&#39;--&#39;, color=&#39;blue&#39;)

        # 隐藏右边和上方的坐标轴线
        ax1.spines[&#39;right&#39;].set_visible(False)
        ax1.spines[&#39;top&#39;].set_visible(False)

        # 添加表格
        col_labels = [&#39;活动名称&#39;, &#39;乐观值&#39;, &#39;最可能值&#39;, &#39;悲观值&#39;]

        cell_text = [[activity.name, activity.optimistic, activity.most_likely, activity.pessimistic] for activity in
                     self.activities]
        table = ax2.table(cellText=cell_text, colLabels=col_labels, loc=&#39;center&#39;)

        # 设置表格的字体大小和行高
        table.auto_set_font_size(False)
        table.set_fontsize(14)

        # # 设置表格的行高为1.5倍原来的高度
        for i in range(len(self.activities) + 1):
            table._cells[(i, 0)].set_height(0.2)
            table._cells[(i, 1)].set_height(0.2)
            table._cells[(i, 2)].set_height(0.2)
            table._cells[(i, 3)].set_height(0.2)

        ax2.axis(&#39;off&#39;)

        # 调整子图之间的间距和边距
        plt.subplots_adjust(hspace=0.3, bottom=0.05)

        # 保存图表
        now = datetime.now().strftime(&#39;%Y%m%d%H%M%S&#39;)
        plt.savefig(&#39;monte_carlo_simulation_{}.png&#39;.format(now))

        # 显示图形
        plt.show()


if __name__ == &#39;__main__&#39;:
    # 模拟参数和变量
    n = 1000000  # 模拟次数

    # 活动的工期分布
    activities = [
        Activity(&#39;活动1&#39;, 5, 10, 7),
        Activity(&#39;活动2&#39;, 3, 8, 5),
        Activity(&#39;活动3&#39;, 2, 6, 4)
    ]

    # 进行蒙特卡洛模拟
    pmp = PMP(activities)
    pmp.monte_carlo_simulation(n)

ログイン後にコピー

以上がPython でモンテカルロシミュレーションを実装する方法と手順の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。