Python を使用して遺伝的アルゴリズムを実装し、巡回セールスマン問題 (TSP) を解決するにはどうすればよいですか?

TSP 問題

それでは、始める前に、この TSP 問題について詳しく説明しましょう。デジタル モデリングを行ったことがある友人や、インテリジェントな最適化や機械学習を経験したことがある友人は、このことを知っているはずです。もちろん、この記事を広く読んでいただけるよう、可能な限り完璧かつ明確にするよう最善を尽くします。ここで実際に問題を解決できるようにします。

したがって、問題は実際には単純で、次のようになります:

N 次元平面では、今日はこの 2 次元平面を使用します。 , この平面上には多くの都市があり、それらの都市は相互に接続されています。次に、すべての都市を訪問するための最短経路を見つける必要があります。たとえば、都市 A、B、C、D、E があるとします。都市間の座標がわかったので、これは都市間の距離を知ることと同じです。次に、すべての都市 A、B、C、D、E への最短経路を作成できるシーケンスを見つけることができます。例えば、計算するとB→A→C→E→Dとなる場合があります。つまり、この順序を求めてください。

列挙

この問題を最初に解決したい場合、実際には多くの解決策がありますが、率直に言うと、パスの合計が最小になる順序を見つける必要があるだけです。たとえば、最初に A を実行し、次に A に最も近いものが B であるかどうかを確認し、次に B に移動し、次に B から移動します。もちろん、これは局所的な貪欲な戦略であり、局所的な最適値に到達するのは簡単です。その後、この時点で DP を検討できます。つまり、A から開始し、その後 2 つの都市が確実に存在することを前提とします。 3 都市が最も短く、4 と 5 が最も短い。最後に、B からも同じことを仮定します。または、すべての状況を直接列挙して距離を計算します。しかし、いずれにせよ、都市の数が増加するにつれてその複雑さは増大するため、現時点では人間の専門知識をコンピューティングに利用させる方法を見つけなければなりません。私はそれを「盲目」と呼んでいます。

インテリジェント アルゴリズム

次に、このインテリジェント アルゴリズムと、それを使用する理由について説明します。前のソリューションでは、大量のデータに対して大量の計算が必要になると述べました。必ずしもそうとは限りませんが、簡単に書くことができます。したがって、現時点では、まず TSP 問題に関して言えば、私たちが望んでいるのはシーケンス、つまり繰り返されないシーケンスです。それでは、現時点では、より単純な解決策はあるのでしょうか? データが十分に大きい場合、それに近いものであれば、必ずしも完全に正確で完全に最小の解決策は必要ありません。したがって、現時点では、従来のアルゴリズムを使用すると、1 つは 1 です。ルールに従って計算するだけで、標準的な答えが何であるかは実際にはわかりません。また、計算を停止するためのしきい値を設定することも困難です。従来のアルゴリズム。しかし、私たち人間には「運」というものがあり、あまりに幸運すぎて、魂に入った瞬間に答えが分からなくなってしまう人もいます。つまり、私たちのインテリジェントなアルゴリズムは実際には「Monkey」に少し似ています。しかし、人々はスキルに注目します。たとえば、経験上、3 つの長いものと 1 つの短いものが最も短いことがわかります。このテクニックを使用して答えを推測することができます。または、ブロガーと同じくらいハンサムなボーイフレンドを探している場合、必要なのは40シリーズの一枚だけです（30でも大丈夫です） グラフィックカードは簡単に取り外せます。孟にはスキルが必要であり、私たちはこれを戦略と呼びます。

戦略

つまり、先ほど話したテクニック、このトリックです。インテリジェント アルゴリズムでは、このマスクが戦略の 1 つです。解決策をより合理的にするには、どうすればそれを取り除くことができるでしょうか?そしてこの時百の花が咲き始める ここではお経は唱えません 最も古典的な 2 つのアルゴリズムを例として取り上げましょう。1 つは遺伝的アルゴリズム、もう 1 つは粒子群アルゴリズム (PSO) です。一例として、彼らは遺伝的アルゴリズムなどのマスク戦略を使用しました。自然選択をシミュレートすることによって、最初にランダムに一連の解と一連の配列を生成し、次に自然選択戦略に基づいてこれらの解をスクリーニングし、次にこれらのソリューションを使用して、新しくてより良いソリューションを見つけてください。このように行ったり来たりした後、最終的に良い解決策を見つけました。粒子群も同様ですが、この部分については実際に使用する際に詳しく説明します。

アルゴリズム

この戦略についてはすでに理解しましたが、アルゴリズムとは何でしょうか?実際、これはこれらの戦略を実装するためのステップであり、コード、ループ、データ構造です。私たちは、TSP のような自然選択、大量の解をランダムに生成する方法など、今述べたことを理解する必要があります。

データ サンプル

わかりました。ここでいくつかの基本的な概念についての説明は終わりました。この時点で、この TSP 問題をどのように表現するかを見てみましょう。これは実際には非常に簡単です。ここでは、テスト データを準備するだけです。ここには 14 の都市があると仮定します。これらの都市のデータは次のとおりです:

    data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
                     22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
                     17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
                     21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))

このデータ セットは、後でテストに使用します。すでに14都市になっています。

それでは、解決策を始めましょう

遺伝的アルゴリズム

わかりました。次に、遺伝的アルゴリズムとは何なのかについて話しましょう。それから、これを使ってこの TSP 問題を解決します。 。

それでは、遺伝的アルゴリズムがどのように騙されるかを見てみましょう。

算法流程

遗传算法其实是在用计算机模拟我们的物种进化。其实更加通俗的说法是筛选，这个就和我们袁老爷爷种植水稻一样。有些个体发育良好，有些个体发育不好，那么我就先筛选出发育好的，然后让他们去繁衍后代，然后再筛选，最后得到高产水稻。其实也和我们社会一样，不努力就木有女朋友就不能保留自己的基因，然后剩下的人就是那些优秀的人和富二代的基因，这就是现实呀。所以得好好学习，天天向上！

那么回到主题，我们的遗传算法就是在模拟这一个过程，模拟一个物竞天择的过程。

所以在我们的算法里面也是分为几大块

繁殖

首先我们的种群需要先繁殖。这样才能不断产生优良基于，那么对应我们的算法，假设我们需要求取

Y = np.sin(10 * x) * x + np.cos(2 * x) * x

的最大值（在一个范围内）那么我们的个体就是一组（X1）的解。好的个体就会被保留，不好的就会被pass，选择标准就是我们的函数 Y 。那么问题来了如何模拟这个过程？我们都知道在繁殖后代的时候我们是通过DNA来保留我们的基因信息，在这个过程当中，父母的DNA交互，并且在这个过程当中会产生变异，这样一来，父母双方的优秀基于会被保存，并且产生的变异有可能诞生更加优秀的后代。

所以接下来我们需要模拟我们的ＤＮＡ，进行交叉和变异。

交叉

这个交叉过程和我们的生物其实很像，当然我们在我们的计算机里面对于数字我们可以将其转化为二进制，当做我们的DNA

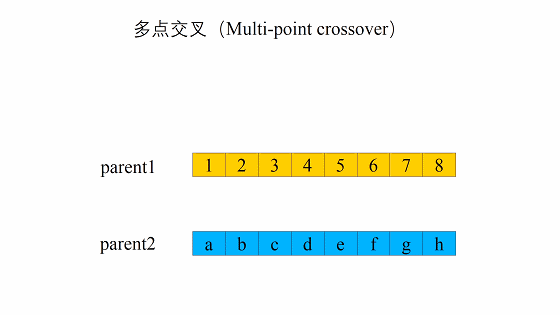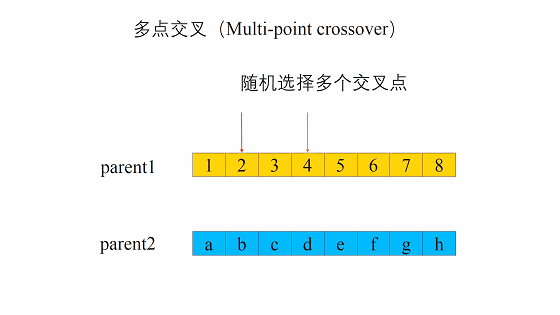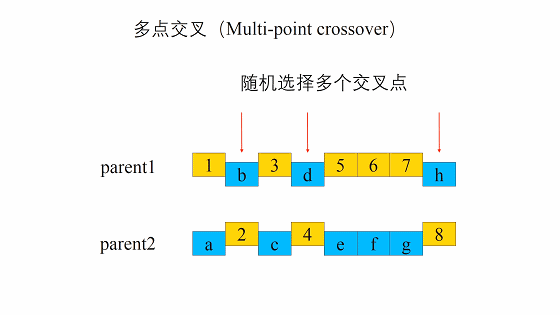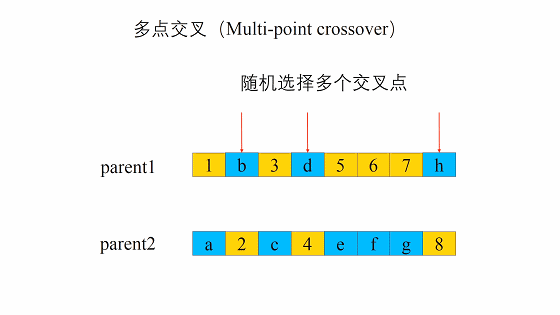
交叉的方式有很多，我们这边选择这一个，进行交叉。

变异

那这个在我们这里就更加简单了

我们只需要在交叉之后，再随机选择几个位置进行改变值就可以了。当然变异的概率是很小的，并且是随机的，这一点要注意。并且由于变异是随机的，所以不排除生成比原来还更加糟糕的个体。

选择

最后我们按照一定的规则去筛选这个些个体就可以了，然后淘汰原来的个体。那么在我们的计算机里面是使用了两个东西，首先我们要把原来二进制的玩意，给转化为我们原来的十进制然后带入我们的函数运算，然后保存起来，之后再每一轮统一筛选一下就好了。

逆转

这个咋说呢，说好听点叫逆转，难听点就算，对于一些新的生成的不好的解，我们是要舍弃的。

代码

那么这部分用代码描述的话就是这样的：

import numpy as np
import matplotlib.pyplot as plt
Population_Size = 100
Iteration_Number = 200
Cross_Rate = 0.8
Mutation_Rate = 0.003
Dna_Size = 10
X_Range=[0,5]
def F(x):
    '''
    目标函数，需要被优化的函数
    :param x:
    :return:
    '''
    return np.sin(10 * x) * x + np.cos(2 * x) * x
def CrossOver(Parent,PopSpace):
    '''
    交叉DNA，我们直接在种群里面选择一个交配
    然后就生出孩子了
    :param parent:
    :param PopSpace:
    :return:
    '''
    if(np.random.rand()) < Cross_Rate:
        cross_place = np.random.randint(0, 2, size=Dna_Size).astype(np.bool)
        cross_one = np.random.randint(0, Population_Size, size=1) #选择一位男/女士交配
        Parent[cross_place] = PopSpace[cross_one,cross_place]
    return Parent
def Mutate(Child):
    &#39;&#39;&#39;
    变异
    :param Child:
    :return:
    &#39;&#39;&#39;
    for point in range(Dna_Size):
        if np.random.rand() < Mutation_Rate:
            Child[point] = 1 if Child[point] == 0 else 0
    return Child
def TranslateDNA(PopSpace):
    &#39;&#39;&#39;
    把二进制转化为十进制方便计算
    :param PopSpace:
    :return:
    &#39;&#39;&#39;
    return PopSpace.dot(2 ** np.arange(Dna_Size)[::-1]) / float(2 ** Dna_Size - 1) * X_Range[1]
def Fitness(pred):
    &#39;&#39;&#39;
    这个其实是对我们得到的F(x)进行换算，其实就是选择的时候
    的概率，我们需要处理负数，因为概率不能为负数呀
    pred 这是一个二维矩阵
    :param pred:
    :return:
    &#39;&#39;&#39;
    return pred + 1e-3 - np.min(pred)
def Select(PopSpace,Fitness):
    &#39;&#39;&#39;
    选择
    :param PopSpace:
    :param Fitness:
    :return:
    &#39;&#39;&#39;
    &#39;&#39;&#39;
    这里注意的是，我们先按照权重去选择我们的优良个体，所以我们这里选择的时候允许重复的元素出现
    之后我们就可以去掉这些重复的元素，这样才能实现保留良种去除劣种。100--》70（假设有30个重复）
    如果不允许重复的话，那你相当于没有筛选
    &#39;&#39;&#39;
    Better_Ones = np.random.choice(np.arange(Population_Size), size=Population_Size, replace=True,
                           p=Fitness / Fitness.sum())
    # np.unique(Better_Ones) #这个是我后面加的
    return PopSpace[Better_Ones]
if __name__ == &#39;__main__&#39;:
    PopSpace = np.random.randint(2, size=(Population_Size, Dna_Size))  # initialize the PopSpace DNA
    plt.ion() 
    x = np.linspace(X_Range, 200)
    # plt.plot(x, F(x))
    plt.xticks([0,10])
    plt.yticks([0,10])
    for _ in range(Iteration_Number):
        F_values = F(TranslateDNA(PopSpace))  
        # something about plotting
        if &#39;sca&#39; in globals():
            sca.remove()
        sca = plt.scatter(TranslateDNA(PopSpace), F_values, s=200, lw=0, c=&#39;red&#39;, alpha=0.5)
        plt.pause(0.05)
        # GA part (evolution)
        fitness = Fitness(F_values)
        print("Most fitted DNA: ", PopSpace[np.argmax(fitness)])
        PopSpace = Select(PopSpace, fitness)
        PopSpace_copy = PopSpace.copy()
        for parent in PopSpace:
            child = CrossOver(parent, PopSpace_copy)
            child = Mutate(child)
            parent[:] = child
    plt.ioff()
    plt.show()

这个代码是以前写的，逆转没有写上（下面的有）

TSP遗传算法

ok,刚刚的例子是拿的解方程，也就是说是一个连续问题吧，当然那个连续处理的话并不是很好，只是一个演示。那么我们这个的话其实类似的。首先我们的ＤＮＡ，是城市的路径，也就是A-B-C-D等等，当然我们用下标表示城市。

种群表示

首先我们确定了使用城市的序号作为我们的个体DNA，例如咱们种群大小为100，有ＡＢＣＤ四个城市，那么他就是这样的，我们先随机生成种群，长这个样：

1 2 3 4
2 3 4 5
3 2 1 4
...

那个1,2,3,4是ABCD的序号。

交叉与变异

这里面的话，值得一提的就是，由于暂定城市需要是不能重复的，且必须是完整的，所以如果像刚刚那样进行交叉或者变异的话，那么实际上会出点问题，我们不允许出现重复，且必须完整，对于我们的DNA，也就是咱们瞎蒙的个体。

代码

由于咱们每一步在代码里面都有注释，所以的话咱们在这里就不再进行复述了。

from math import floor
import numpy as np
import matplotlib.pyplot as plt
class Gena_TSP(object):
    """
    使用遗传算法解决TSP问题
    """
    def __init__(self, data, maxgen=200,
                 size_pop=200, cross_prob=0.9,
                 pmuta_prob=0.01, select_prob=0.8
                 ):
        self.maxgen = maxgen            # 最大迭代次数
        self.size_pop = size_pop        # 群体个数，（一次性瞎蒙多少个解）
        self.cross_prob = cross_prob    # 交叉概率
        self.pmuta_prob = pmuta_prob    # 变异概率
        self.select_prob = select_prob  # 选择概率
        self.data = data        # 城市的坐标数据
        self.num = len(data)    # 有多少个城市，对应多少个坐标，对应染色体的长度（我们的解叫做染色体）
        """
        计算城市的距离，我们用矩阵表示城市间的距离
        """
        self.__matrix_distance = self.__matrix_dis()
        self.select_num = int(self.size_pop * self.select_prob)
        # 通过选择概率确定子代的选择个数
        """
        初始化子代和父代种群，两者相互交替
        """
        self.parent = np.array([0] * self.size_pop * self.num).reshape(self.size_pop, self.num)
        self.child = np.array([0] * self.select_num * self.num).reshape(self.select_num, self.num)
        """
        负责计算每一个个体的（瞎蒙的解）最后需要多少距离
        """
        self.fitness = np.zeros(self.size_pop)
        self.best_fit = []
        self.best_path = []
        # 保存每一步的群体的最优路径和距离
    def __matrix_dis(self):
        """
        计算14个城市的距离，将这些距离用矩阵存起来
        :return: 
        """
        res = np.zeros((self.num, self.num))
        for i in range(self.num):
            for j in range(i + 1, self.num):
                res[i, j] = np.linalg.norm(self.data[i, :] - self.data[j, :])
                res[j, i] = res[i, j]
        return res
    def rand_parent(self):
        """
        初始化种群
        :return:
        """
        rand_ch = np.array(range(self.num))
        for i in range(self.size_pop):
            np.random.shuffle(rand_ch)
            self.parent[i, :] = rand_ch
            self.fitness[i] = self.comp_fit(rand_ch)
    def comp_fit(self, one_path):
        """
        计算，咱们这个路径的长度，例如A-B-C-D
        :param one_path:
        :return:
        """
        res = 0
        for i in range(self.num - 1):
            res += self.__matrix_distance[one_path[i], one_path[i + 1]]
        res += self.__matrix_distance[one_path[-1], one_path[0]]
        return res
    def out_path(self, one_path):
        """
        输出我们的路径顺序
        :param one_path:
        :return:
        """
        res = str(one_path[0] + 1) + '-->'
        for i in range(1, self.num):
            res += str(one_path[i] + 1) + '-->'
        res += str(one_path[0] + 1) + '\n'
        print(res)
    def Select(self):
        """
        通过我们的这个计算的距离来计算出概率，也就是当前这些个体DNA也就瞎蒙的解
        之后我们在通过概率去选择个体，放到child里面
        :return:
        """
        fit = 1. / (self.fitness)  # 适应度函数
        cumsum_fit = np.cumsum(fit)
        pick = cumsum_fit[-1] / self.select_num * (np.random.rand() + np.array(range(self.select_num)))
        i, j = 0, 0
        index = []
        while i < self.size_pop and j < self.select_num:
            if cumsum_fit[i] >= pick[j]:
                index.append(i)
                j += 1
            else:
                i += 1
        self.child = self.parent[index, :]
    def Cross(self):
        """
        模仿DNA交叉嘛，就是交换两个瞎蒙的解的部分的解例如
        A-B-C-D
        C-D-A-B
        我们选几个交叉例如这样
        A-D-C-B
        1,3号交换了位置，当然这里注意可不能重复啊
        :return:
        """
        if self.select_num % 2 == 0:
            num = range(0, self.select_num, 2)
        else:
            num = range(0, self.select_num - 1, 2)
        for i in num:
            if self.cross_prob >= np.random.rand():
                self.child[i, :], self.child[i + 1, :] = self.intercross(self.child[i, :],
                                                                             self.child[i + 1, :])
    def intercross(self, ind_a, ind_b):
        """
        这个是我们两两交叉的具体实现
        :param ind_a:
        :param ind_b:
        :return:
        """
        r1 = np.random.randint(self.num)
        r2 = np.random.randint(self.num)
        while r2 == r1:
            r2 = np.random.randint(self.num)
        left, right = min(r1, r2), max(r1, r2)
        ind_a1 = ind_a.copy()
        ind_b1 = ind_b.copy()
        for i in range(left, right + 1):
            ind_a2 = ind_a.copy()
            ind_b2 = ind_b.copy()
            ind_a[i] = ind_b1[i]
            ind_b[i] = ind_a1[i]
            x = np.argwhere(ind_a == ind_a[i])
            y = np.argwhere(ind_b == ind_b[i])
            if len(x) == 2:
                ind_a[x[x != i]] = ind_a2[i]
            if len(y) == 2:
                ind_b[y[y != i]] = ind_b2[i]
        return ind_a, ind_b
    def Mutation(self):
        """
        之后是变异模块，这个就是按照某个概率，去替换瞎蒙的解里面的其中几个元素。
        :return:
        """
        for i in range(self.select_num):
            if np.random.rand() <= self.cross_prob:
                r1 = np.random.randint(self.num)
                r2 = np.random.randint(self.num)
                while r2 == r1:
                    r2 = np.random.randint(self.num)
                self.child[i, [r1, r2]] = self.child[i, [r2, r1]]
    def Reverse(self):
        """
        近化逆转，就是说下一次瞎蒙的解如果没有更好的话就不进入下一代，同时也是随机选择一个部分的
        我们不是一次性全部替换
        :return: 
        """
        for i in range(self.select_num):
            r1 = np.random.randint(self.num)
            r2 = np.random.randint(self.num)
            while r2 == r1:
                r2 = np.random.randint(self.num)
            left, right = min(r1, r2), max(r1, r2)
            sel = self.child[i, :].copy()
            sel[left:right + 1] = self.child[i, left:right + 1][::-1]
            if self.comp_fit(sel) < self.comp_fit(self.child[i, :]):
                self.child[i, :] = sel
    def Born(self):
        """
        替换，子代变成新的父代
        :return:
        """
        index = np.argsort(self.fitness)[::-1]
        self.parent[index[:self.select_num], :] = self.child
def main(data):
    Path_short = Gena_TSP(data)     # 根据位置坐标，生成一个遗传算法类
    Path_short.rand_parent()        # 初始化父类
    ## 绘制初始化的路径图
    fig, ax = plt.subplots()
    x = data[:, 0]
    y = data[:, 1]
    ax.scatter(x, y, linewidths=0.1)
    for i, txt in enumerate(range(1, len(data) + 1)):
        ax.annotate(txt, (x[i], y[i]))
    res0 = Path_short.parent[0]
    x0 = x[res0]
    y0 = y[res0]
    for i in range(len(data) - 1):
        plt.quiver(x0[i], y0[i], x0[i + 1] - x0[i], y0[i + 1] - y0[i], color=&#39;r&#39;, width=0.005, angles=&#39;xy&#39;, scale=1,
                   scale_units=&#39;xy&#39;)
    plt.quiver(x0[-1], y0[-1], x0[0] - x0[-1], y0[0] - y0[-1], color=&#39;r&#39;, width=0.005, angles=&#39;xy&#39;, scale=1,
               scale_units=&#39;xy&#39;)
    plt.show()
    print(&#39;初始染色体的路程: &#39; + str(Path_short.fitness[0]))
    # 循环迭代遗传过程
    for i in range(Path_short.maxgen):
        Path_short.Select()     # 选择子代
        Path_short.Cross()      # 交叉
        Path_short.Mutation()   # 变异
        Path_short.Reverse()    # 进化逆转
        Path_short.Born()      # 子代插入
        # 重新计算新群体的距离值
        for j in range(Path_short.size_pop):
            Path_short.fitness[j] = Path_short.comp_fit(Path_short.parent[j, :])
        index = Path_short.fitness.argmin()
        if (i + 1) % 50 == 0:
            print(&#39;第&#39; + str(i + 1) + &#39;步后的最短的路程: &#39; + str(Path_short.fitness[index]))
            print(&#39;第&#39; + str(i + 1) + &#39;步后的最优路径:&#39;)
            Path_short.out_path(Path_short.parent[index, :])  # 显示每一步的最优路径
        # 存储每一步的最优路径及距离
        Path_short.best_fit.append(Path_short.fitness[index])
        Path_short.best_path.append(Path_short.parent[index, :])
    return Path_short  # 返回遗传算法结果类
if __name__ == &#39;__main__&#39;:
    data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
                     22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
                     17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
                     21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))
    main(data)

运行结果

ok,我们来看看运行的结果：

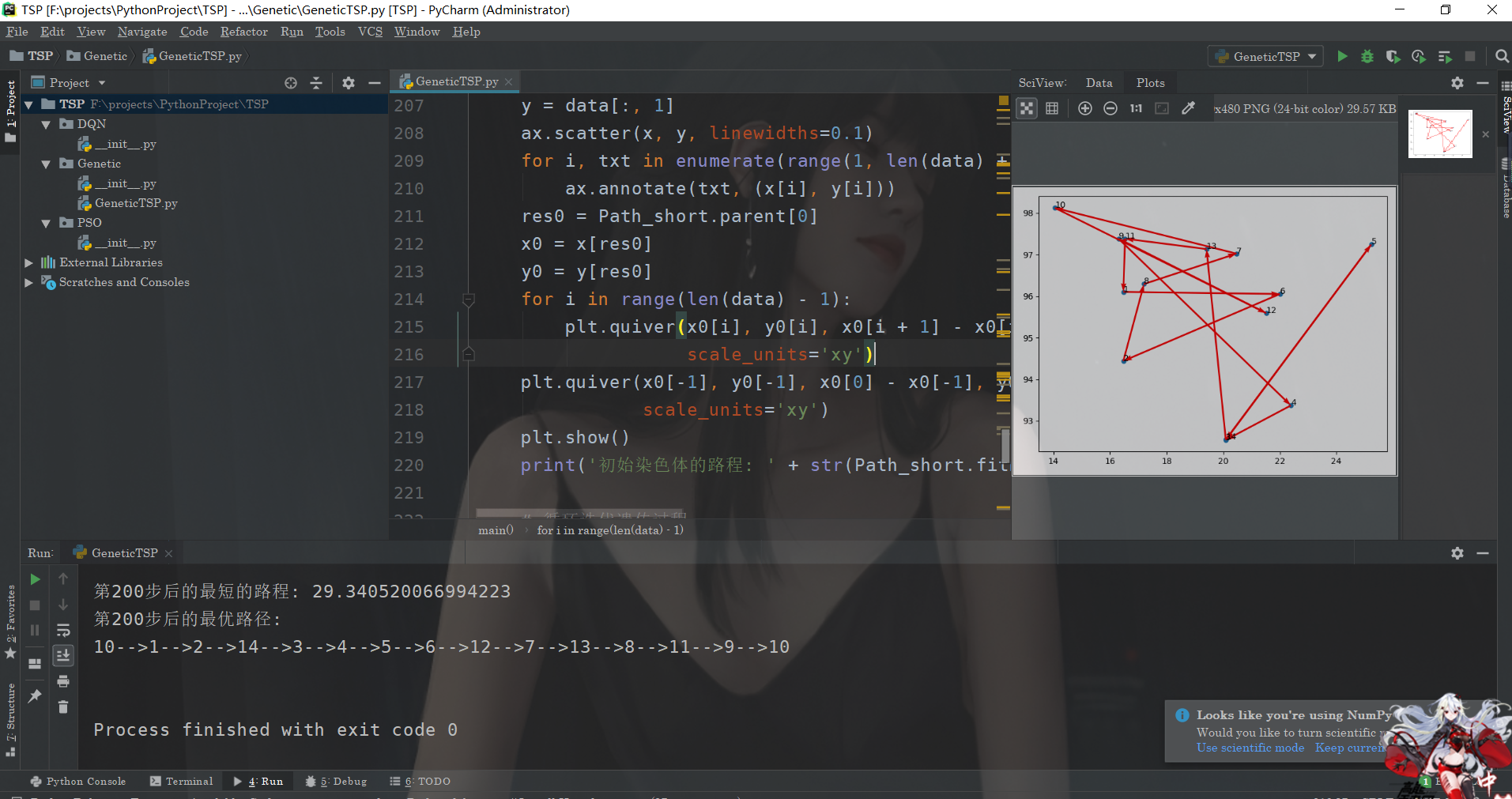
以上がPython を使用して遺伝的アルゴリズムを実装し、巡回セールスマン問題 (TSP) を解決するにはどうすればよいですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。