Python でニワトリの群れアルゴリズムを実装する方法-Python チュートリアル-php.cn

アルゴリズムの紹介

CSO (Chicken Swarm Optimization) と略されるチキン群れ最適化は、いわゆるバイオニクスの背景を持っていますが、本質的には粒子群アルゴリズムの変形です。

簡単に言えば、粒子群は粒子の集まりです。各粒子には独自の位置と速度があり、各粒子は最適な粒子に引き付けられる必要があります。これら 2 つのルールに加えて、粒子は完全に一致しています。位置と速度を除いて、互いに等しい。

もちろん、粒子群アルゴリズム自体もバイオニクスの背景があり、餌を食べる鳥の群れからインスピレーションを得ていると言われていますが、もちろんそれは重要ではありません。粒子が同等の鳥のグループに変わります。

ニワトリの群れのアルゴリズムは、これらの粒子または鳥に異なるアイデンティティ特性を追加するため、それらはもはや互いに等価ではなくなります。

鶏の群れには少なくとも 3 つのクラス (雄鶏、雌鶏、ひよこ) があり、それぞれの鶏は独自の位置と速度を持っています。しかし、違うのは、

雄鶏が最も雄大であるということです。基本的には自由に歩き回ることができますが、時々他の雄鶏に気づくと、次のような考えを抱くことがあります。食べ物をつかむことはランダムに相当し、他の雄鶏の 1 匹を描くとその位置に影響を与えます。
雌鶏が最も苦しんでおり、一方では雄鶏のリーダーシップを受け入れなければならず、他方では食べ物をめぐって他の雌鶏と競争しなければなりません。
小鶏は最も気楽で、鶏に従っているだけです。

位置関係が変わると、雌鶏やひよこは本来のリーダーを徐々に忘れ、個体数関係も変化する可能性があります。

Python はニワトリとニワトリの群れを実装します

まず第一に、ニワトリクラスを実装する必要があります。ニワトリには 2 つの基本属性、つまり場所とカテゴリがあります。

import numpy as np
from random import gauss, random
randint = np.random.randint
uniRand = np.random.uniform

class Chicken:
    def __init__(self, N, xRange, order=0, kind=0):
        # 生成(N)维参数
        self.x = uniRand(*xRange, (N,))
        self.best = np.inf
        self.xBest = np.zeros((N,))
        self.kind = kind            # 鸡的类别
        self.order = order          # 鸡的编号
    
    # 设置自己的首领公鸡
    def setCock(self, i):
        self.cock = i

    # 设置自己的监护母鸡
    def setHen(self, i):
        self.hen = i

ログイン後にコピー

種類は、雄鶏、雌鶏、ひよこの 3 つのカテゴリに分類されます。その中で、各雌鶏には独自のアルファ雄鶏がおり、各雛には独自の守護鶏がいます。

order は鶏の群れの中のこの鶏の番号で、主に鶏の群れに反映されます。

鶏の群れと粒子の群れには大きな違いがあります。最終的には、群れは 1 つだけです。鶏の群れでは、それぞれの雄鶏が独自の雌鶏とひよこを持ちます。これは、小さな鶏の群れに相当します。グループ。ただし、ニワトリ間の関係はニワトリ自身に依存しないため、ニワトリの群れに実装する必要があります。

randint = np.random.randint
class Swarm:
    # cNum 鸡数，是三个元素的列表，分别是公鸡、母鸡和小鸡数
    # N参数维度
    def __init__(self, cNum, N, xRange):
        self.initCs(cNum, N, xRange)
        self.bestCS = deepcopy(self.cs)     #最佳鸡群
        self.best = np.inf  #全局最优值
        self.xBest = np.zeros((N,)) #全局最优参数
        self.N = N

    def initCs(self, cNum, N, xRange, vRange):
        self.cs = []
        self.cNum = cNum
        self.cocks = np.arange(cNum[0])     # 公鸡编号
        self.hens = np.arange(cNum[0], cNum[0]+cNum[1]) #母鸡编号
        self.chicks = np.arange(cNum[0]+cNum[1], np.sum(cNum))  #小鸡编号
        kinds = np.repeat([0,1,2], cNum)
        for i in range(sum(cNum)):
            self.cs.append(Chicken(N,xRange, vRange, i, kinds[i]))
            if kinds[i] > 0:
                cock = randint(0, cNum[0])
                self.cs[i].setCock(cock)
            if kinds[i] > 1:
                hen = randint(cNum[0], cNum[0]+cNum[1])
                self.cs[i].setHen(hen)

ログイン後にコピー

このうち、initCs はニワトリとニワトリの群れを初期化する関数です。ニワトリのリーダー、オンドリ、ヒヨコの守護鶏はランダムに生成されます。

ニワトリの群れの更新

次のステップはアルゴリズムの中核部分です。ニワトリごとに異なる更新ルールに従う必要があります。その中でもオンドリが最もクールであり、その次の位置は次の条件にのみ依存します。自分自身と他のニワトリ、ランダムに選ばれたオンドリ。

cock

現在のオンドリの番号が i で、ランダムに選択されたオンドリの番号が j (j≠i) であることを思い出してください。 i 番目のオンドリの位置は

#xxx

i_{(t 1)=x}i_{(t)⋅(1 r)}

です。、r は正規分布によって生成されます。乱数は 1ΣN(0,Σ

2^{) として表すことができます。ここで、Σ}2^は

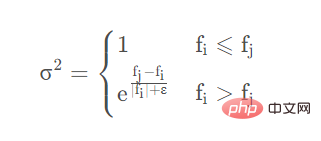Python でニワトリの群れアルゴリズムを実装する方法 # このうち、f は一般に適応度係数と呼ばれるもので、検索対象の関数にあるニワトリを詰め込んだ値に相当します。たとえば、y=

の最小値を検索する場合、ニワトリの現在位置が 1.5 の場合、f=1.5²=2.25 となります。 ε は、ゼロ除算エラーを防ぐ小さな量です。ただし、上記のすべての x はスカラーを表すのではなく、配列を表すことに注意してください。

Python の実装は

# 写在Swarm类中
def cockStep(self):
    for i in self.cocks:
        # 第j只公鸡
        j = np.random.randint(self.cNum[0])
        if j==i:
            j = (j+1) % self.cNum[0]
        # 第i只公鸡
        ci = self.cs[i]
        # 第j只公鸡
        cj = self.cs[self.cocks[j]]
        sigma = 1 if cj.best > ci.best else np.exp(
            (cj.best-ci.best)/(np.abs(ci.best)+1e-15))
        ci.x *= 1 + gauss(0, sigma)

ログイン後にコピー

Hen

現在の雌鶏番号が i であるとします。この雌鳥はリーダーのオンドリに従うだけでなく、他の鶏と餌を奪い合う。

#xx

(t 1)=x

i_{(t) k}1_r1_(xc_−xi_{) k}2_r2_(xj_−xi₎_{このうち、x}c

はリーダーの雄鶏で、x

j_{は別の雌鶏または雄鶏です。 k}1_,k2_{は係数であり、更新ロジックは rooster と同じで、f}i_{が大きい場合は} と表されます。

コードは Python でニワトリの群れアルゴリズムを実装する方法

def henStep(self):
    nGuarder = self.cNum[0] + self.cNum[1] - 2
    for i in self.hens:
        guarders = list(self.cocks) + list(self.hens)
        c = self.cs[i].cock     #首领公鸡
        guarders.remove(i)
        guarders.remove(c)
        # 随机生成另一只监护鸡
        j = guarders[np.random.randint(nGuarder)]
        ci = self.cs[i]
        cj = self.cs[j]
        cc = self.cs[c]
        k1, k2 = random(), random()
        if cc.best > ci.best:
            k1 *= np.exp((ci.best-cc.best)/(np.abs(ci.best)+1e-15))
        if cj.best < ci.best:
            k2 *=  np.exp(cj.best-ci.best)
        ci.x += k1*(cc.x-ci.x)+k2*(cj.x-ci.x)

ログイン後にコピー

小鸡

として実装されています。最後はチキンの更新ロジックです。鶏の餌の周りを見て、その更新ロジックは #xxx

(t 1)=x

(t) r(x_h(t) −x_i(t)) このうち、x_h はガーディアン編、r は乱数、アルゴリズムは

def chickStep(self):
    for i in self.chicks:
        ci = self.cs[i]
        ci.x += 2*random()*(self.cs[ci.hen].x-ci.x)

ログイン後にコピー

として実装されます。

_{鶏群全体へ}

「アルゴリズムは命から生まれ、命よりも高い」という言葉の通り、本来は年功序列が重視されますが、鶏群のアルゴリズムでは強さが求められます。まさに強調点です。運が良く、ニワトリがオンドリよりも優れた最適化結果を得た場合、ニワトリはオンドリに進化します。言い換えれば、時々、群れ内の鶏のアイデンティティが再配置されます。最適化効果が最も優れているのはリーダーの鶏で、最も悪いのは番鶏であり、最も悪いのは番鶏です。最悪なのはオンドリだけです。今はニワトリです。

def update(self):
    cn = np.sum(self.cNum)
    c1, c2 = self.cNum[0], self.cNum[0]+self.cNum[1]
    fitness = [self.cs[i].best for i in range(cn)]
    index = np.argsort(fitness)
    self.cocks = index[np.arange(c1)]
    self.hens = index[np.arange(c1,c2)]
    self.chicks = index[np.arange(c2,cn)]
    for i in self.cocks:
        self.cs[i].kind = 0
    for i in self.hens:
        self.cs[i].kind = 1
    for i in self.chicks:
        self.cs[i].kind = 2
    for i in range(cn):
        if self.cs[i].kind > 0:
            cock = self.cocks[randint(0, c1)]
            self.cs[i].setCock(cock)
        if self.cs[i].kind > 1:
            hen = self.hens[randint(c1,c2)]
            self.cs[i].setHen(hen)

ログイン後にコピー

最適化の反復

この時点で、クラスターアルゴリズムのフレームワークは正常に確立されました。次に、最も重要な部分である最適化が実装されます。

其基本逻辑是，输入一个待优化func，通过将每只鸡的位置x带入到这个函数中，得到一个判定值，最后通过这个判定值，来不断更新鸡群。

除了这个函数之外，还需要输入一些其他参数，比如整个鸡群算法的迭代次数，以及鸡群更新的频次等等

# func为待优化函数
# N为迭代次数
# T为鸡群更新周期
def optimize(self, func, N, T, msgT):
    for n in range(N):
        # 计算优化参数
        for c in self.cs:
            c.best = func(c.x)
        # 分别更新公鸡、母鸡和小鸡
        self.cockStep()
        self.henStep()
        self.chickStep()
        if (n+1)%T == 0:
            self.update()   #每T次更新一次种群
            self.printBest(n)
    self.printBest(n)

ログイン後にコピー

其中，printBest可以将当前最佳结果打印出来，其形式为

def printBest(self,n):
    fitness = [c.best for c in self.cs]
    best = np.min(fitness)
    ind = np.where(fitness==best)[0]
    msg = f"已经迭代{n}次，最佳优化结果为{np.min(fitness)}，参数为：\n"
    msg += ", ".join([f"{x:.6f}" for x in self.cs[ind].x])
    print(msg)

ログイン後にコピー

测试

算法完成之后，当然要找个函数测试一下，测试函数为

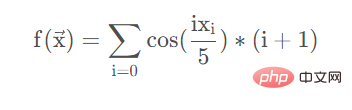
Python でニワトリの群れアルゴリズムを実装する方法

def test(xs):
    _sum = 0.0
    for i in range(len(xs)):
        _sum = _sum + np.cos((xs[i]*i)/5)*(i+1)
    return _sum

if __name__ == "__main__":
    cNum = [15,20,100]
    s = Swarm(cNum, 5, (-5,5))
    s.optimize(test, 20, 5)

ログイン後にコピー

测试结果如下

已经迭代4次，最佳优化结果为-5.793762423022024，参数为：
-6.599526, 3.117137, 5.959538, 7.225785, 5.204990
已经迭代9次，最佳优化结果为-10.61594651972434，参数为：
-7.003724, -5.589730, 0.981409, 12.920325, -19.006112
已经迭代14次，最佳优化结果为-9.143596747975293，参数为：
5.388234, -3.714421, -5.254391, -5.216215, -6.079223
已经迭代19次，最佳优化结果为-11.097888385616995，参数为：
-9.156244, -5.914600, -5.960154, 4.550833, 4.127889
已经迭代19次，最佳优化结果为-11.097888385616995，参数为：
-9.156244, -5.914600, -5.960154, 4.550833, 4.127889

以上がPython でニワトリの群れアルゴリズムを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。