統合されたマルチグラフ ニューラル ネットワーク

#1. 統一された観点からの GNN
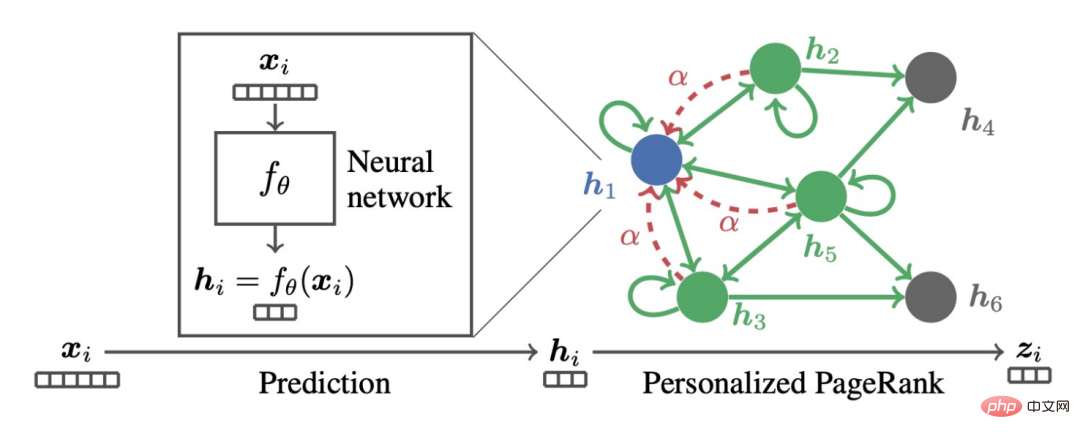
#1. 既存の GNN 伝播パラダイムGNN は空域でどのように伝播しますか?以下の図に示すように、ノード A を例として取り上げます。
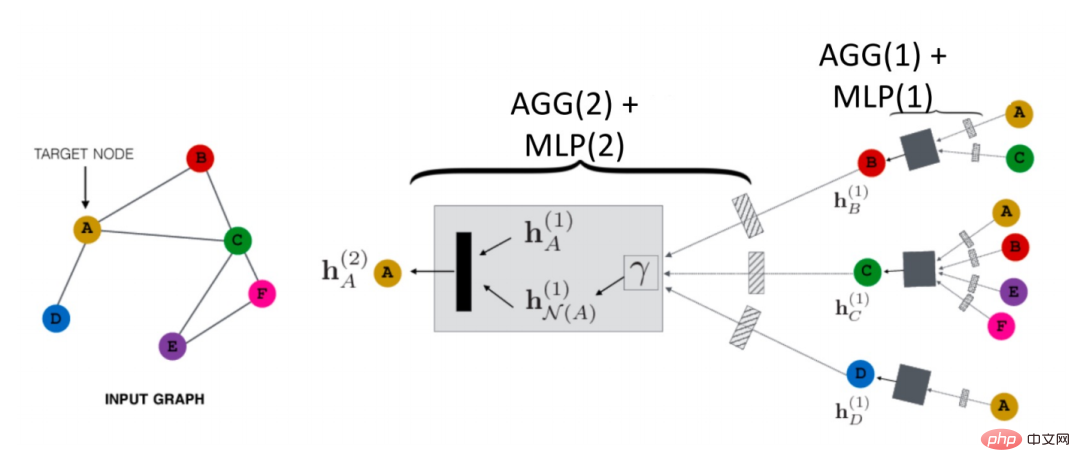
##まず、ノード A を識別します。その近隣ノード N (A) の情報は # hN(A)# に集約されます。 ##(1 ) を A と組み合わせて上位層 h## を表しますN(A)(1) が結合され、変換関数 (つまり、式内の Trans(・)) を通じて、次のレベルの表現が得られます。 A が得られます hN(A)(2)。これは最も基本的な GCN 伝播パラダイムです。
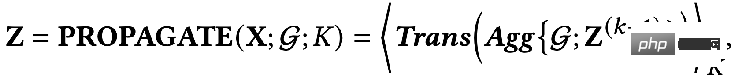 さらに、分離された伝播プロセスがあります。
さらに、分離された伝播プロセスがあります。
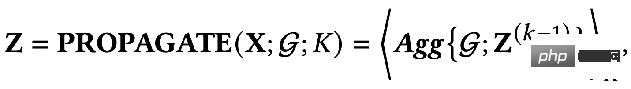
##これら 2 つの違いは何ですか?
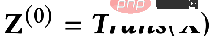 分離伝播パラダイムでは、最初に特徴抽出器、つまり変換関数を使用して初期特徴を抽出し、次に抽出された特徴が集計のために集計関数に入れられます。この方法では、特徴抽出と集約が分離されます。つまり、分離が実現されます。この利点は次のとおりです。
分離伝播パラダイムでは、最初に特徴抽出器、つまり変換関数を使用して初期特徴を抽出し、次に抽出された特徴が集計のために集計関数に入れられます。この方法では、特徴抽出と集約が分離されます。つまり、分離が実現されます。この利点は次のとおりです。
#以前の変換関数を自由に設計し、任意のモデルを使用できます。
- 集計中に多くのレイヤーを追加して、より遠くの接続情報を取得できますが、集計関数には次のようなパラメータがあるため、過剰なパラメータ化のリスクに直面することはありません。最適化するパラメータはありません。
- 上記は 2 つの主要なパラダイムであり、ノードの埋め込み出力ではネットワークの最後の層または中間層の残差を使用できます。層です。
##上記のレビューを通じて、GNN には 2 つの基本的な情報ソースがあることがわかります。
ネットワークのトポロジ構造: 一般に、グラフ構造の一致する情報属性を取得できます。
- # ノードの特性: 一般に、ノードの低周波信号と高周波信号が含まれます。
- #2. 統合された最適化フレームワーク GNN の伝播メカニズムに基づいて、次のことが可能です。既存の GNN には 2 つの共通の目標があることがわかります:
- ノードの特性から有益な情報をエンコードします。
- #トポロジのスムージング機能を使用します。
では、これら 2 つの目標を数学的な言語を使って説明できるでしょうか?誰かが次の式で表される GNN 最適化統合フレームワークを提案しました。

## 最初のもの最適化目標の項目:

は特徴フィッティング項目であり、その目標は学習されたノードを作成することであることを示しますZ は元のフィーチャ H に可能な限り近く、F#1#、F##2 は、次のことができるグラフ畳み込みです。核を自由に設計できる。畳み込みカーネルが単位行列 I の場合はオールパス フィルター、畳み込みカーネルが 0 行列の場合はローパス フィルター、畳み込みカーネルがラプラシアン行列 L の場合はローパス フィルターと等価です。ハイパスフィルター。
最適化目標の 2 番目の項は、形式的には行列のトレースであり、その関数はグラフ上の通常の項です。トレースと通常の用語の違いは何ですか?関係性はどうですか?実際、2 番目の項目は次の形式に展開されます。

##意味は、次のとおりです。キャプチャされた画像 隣接する 2 つのノード間の特徴の違いの程度は、グラフの滑らかさを表します。この目標を最小限に抑えることは、私と隣人をより似たものにすることと同じです。 3. 統合最適化フレームワークを使用して既存の GNN を理解する
ほとんどの GNN がこの目標を最適化しています。さまざまな状況で議論してください:
# パラメータが次の場合:

最適化目標が次のようになった場合:

##偏導関数を見つけて次を取得します。

上記を見てみましょう。結果はさらに拡張できます。

その意味は、K 番目の層を意味します。すべてのノード表現は伝播プロセスに等しいです。最後まで導出すると、特徴量変換 W* 完了後に隣接行列上を K 回伝播した初期特徴量 X と等しいことがわかります。実際、これは GCN または SGC のモデルから非線形層を取り除いたものです。
パラメータ F1=F2=I, ξ=1, ξ=1/α-1 の場合、α∈(0,q]、オールパス フィルターを選択すると、最適化目標は次のようになります:

このとき、Z の偏導関数も求め、その偏導関数を 0 にすると、閉次式が得られます。最適化目標の形式ソリューション:

結果をわずかに変換すると、次のようになります。次の式:

上記の式は、ノードの特徴が伝播するプロセスを表していることがわかります。パーソナライズされた PageRank を使用する、それが PPNP モデルです。

同様のモデルも同様です。勾配降下法を使用してそれを見つけると、 set ステップ サイズは b で、反復項は Z に関する時間 k-1 での目的関数の偏導関数です。 ####################################いつ #############
## になると次のものが得られます: 
##これは APPNP モデルです。 APPNP モデルが登場した背景には、PPNP モデルにおける行列の逆演算が複雑すぎるため、APPNP では反復近似を使用してそれを解決しています。 APPNP は両方とも同じフレームワークに由来しているため、APPNP が PPNP に収束できることも理解できます。 
#4. 新しい GNN フレームワーク

新しい適合項 O
##fit

を設計し、対応するグラフ正規項
#reg を使用し、新しい GNN モデルを取得するための新しい解法プロセスを追加します。 ① 例 1: オールパス フィルタリングからローパス フィルタリングまで前述したように、すべてのデバイス F1#=
F の下にフィルタリング Convolution カーネルを渡します
2=I 、畳み込みカーネルがラプラシアン行列 L の場合ハイパスフィルターです。これら 2 つの状況を重み付けして得られた GNN がローパス情報をエンコードできる場合: # #いつ ################## で正確な解決策を取得できます:

#同様に、これを反復的に解決できます:

#5, Elastic GNN
以前の統一フレームワークで述べた正規項は、計算グラフ上の任意の 2 点間の差分情報に相当する L2 正規項に相当します。研究者の中には、L2 正則化がグローバルすぎるため、グラフ全体の滑らかさが同じになる傾向があり、現実と完全に一致しているわけではないと感じている人もいます。したがって、グラフ内の比較的大きな変化にペナルティを与える L1 定期項を追加することが提案されました。

L1 定期期間部分は次のとおりです:

#つまり、上記の統合フレームワークは次のことを示しています:
よりマクロな視点を使用して GNN を理解できます
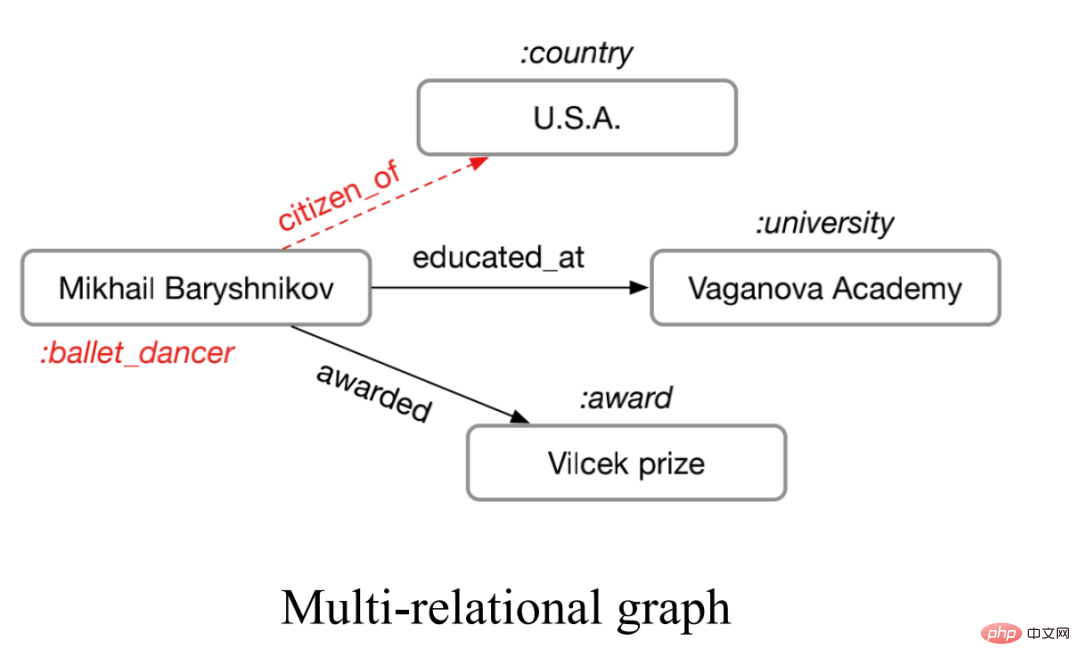
ただし、この統一フレームワークは、同種のグラフ構造にのみ適用できます。次に、より一般的なマルチリレーションシップ グラフ構造を見てみましょう。 2. リレーショナル GNN モデル
1、RGCN
##いわゆるマルチリレーションシップ グラフとは、次の図に示すように、エッジ タイプが 1 より大きいグラフを指します。
 #この種の多重関係図は、現実の世界で非常に広く普及しています。化学分子における複数の種類の分子結合。社会関係図における人々の間のさまざまな関係など。このようなグラフの場合、リレーショナル グラフ ニューラル ネットワークを使用してモデル化できます。主なアイデアは、N 個の関係を持つグラフを個別に集計して N 個の集計結果を取得し、その N 個の結果を集計することです。
#この種の多重関係図は、現実の世界で非常に広く普及しています。化学分子における複数の種類の分子結合。社会関係図における人々の間のさまざまな関係など。このようなグラフの場合、リレーショナル グラフ ニューラル ネットワークを使用してモデル化できます。主なアイデアは、N 個の関係を持つグラフを個別に集計して N 個の集計結果を取得し、その N 個の結果を集計することです。
 式で表すと次のようになります:
式で表すと次のようになります:
 集計が 2 つのステップで実行されることがわかります。まず、すべての関係 R から関係 r を選択し、次に、次の関係を含む関係を見つけます。すべてのノード
集計が 2 つのステップで実行されることがわかります。まず、すべての関係 R から関係 r を選択し、次に、次の関係を含む関係を見つけます。すべてのノード
Nr が集約され、そのうち Wr は、さまざまな関係に重みを付けるために使用される重みです。したがって、グラフ内の関係の数が増加すると、重み行列 Wr も増加し、問題が発生することがわかります。オーバーパラメータ化 (オーバーパラメータ化)。さらに、関係に従ってトポロジ関係図を分割すると、過度の平滑化が発生する可能性があります。 2、CompGCN
#過剰パラメータ化の問題を解決するために、CompGCN はベクトル化された関係エンコーダーを使用して N 関係行列を置き換えます:

エンコーダには、順方向、逆方向、自己ループの 3 方向の関係が含まれています。

繰り返しのたびに、リレーションの埋め込みも更新されます。

しかし、このヒューリスティックな設計とそのようなパラメトリック エンコーダは、過剰なパラメータ化を引き起こす可能性もあります。次に、上記の考慮事項に基づいて、最適化目標の観点からより信頼性の高い GNN を設計し、同時に既存の GNN の問題を解決できるかという作業の開始点を取得します。
3. 統合されたマルチリレーションシップ グラフ ニューラル ネットワーク
当社の EMR GNN は今年公開されました。マルチリレーションシップ グラフに適した GCN を設計する方法について、主に次の 3 つの側面に焦点を当てます。
- 適切な統合最適化アルゴリズムを設計する方法
- メッセージ配信メカニズム
- #GNN モデルの設計方法
1. 統合された最適化アルゴリズム
この最適化アルゴリズムは、次の 2 つの要件を満たす必要があります:
- 複数の関係をグラフ上で同時にキャプチャできるようになります
- 重要度をモデル化できるようになりますグラフ上のさまざまな関係の
マルチリレーションシップ グラフ上で提案する統合マルチリレーションシップ グラフの正規項は次のとおりです。

この通常の用語もグラフ信号の平滑化能力を捉えるためのものですが、この隣接行列は関係 r の下でキャプチャされ、正規化の対象となります 制約付きパラメータ #μr は、特定の関係の重要性をモデル化することです。 2 番目の項は、係数ベクトルの第 2 正規形正則化であり、係数ベクトルをより均一にするものです。
#過剰平滑化の問題を解決するために、元の特徴情報が失われないように適切な用語を追加しました。フィッティング項と正規項の合計は次のとおりです:

これは、次のとおりです。前の章 統一フレームワークと比較すると、ここで設計する目的関数には、ノード補正 Z と関係行列パラメーター μ の 2 つの変数が含まれています。したがって、そのような最適化目標に基づいてメッセージ伝播メカニズムを導き出すことも課題です。 2. メッセージ受け渡しメカニズムの導出
ここでは、反復最適化戦略を採用します:
- ##最初にノード表現 Z を修正し、次にパラメータ μを最適化します。
- 次に、前の結果 μ に基づいてノードを最適化します。 iteration Represent Z
固定ノードが Z を表す場合、最適化目標全体は、制約付き目的関数のみに関連する目的関数に縮退します。

これは実際には単体制約 (単体上のμの標準 A 凸関数の制約) です。このタイプの問題は、ミラー エントロピー降下法アルゴリズムを使用して解決できます。最初に定数を見つけてから、各関係に基づいて重み係数を更新します。更新プロセス全体は指数関数的勾配降下法アルゴリズムに似ています。

関係係数 μ を修正して Z を更新すると、最適化目標は次のように縮退します。この形式:

このようにして、目的関数の偏導関数を求めます。 Z に変換し、偏導関数が 0 に等しい場合、次の結果を得ることができます。 Z の閉じた形式の解は次のようになります。

同様に、反復を使用して次のことができます。近似解を求める このプロセスは次のように表現できます:

派生メッセージよりメカニズムを通過させることで、設計が過剰なスムーズを回避し、過剰なパラメータ化を回避できることを証明できます。以下では証明プロセスを見ていきます。
元のマルチリレーションシップ PageRank マトリックスは次のように定義されます:

パーソナライズされたマルチリレーションシップ PageRank マトリックスは、これに基づいて独自のノードを返す確率を追加します:

上記の循環方程式を解くことで、マルチリレーションシップのパーソナライズされた PageRank マトリクスを取得できます。 ### ##################私たちにさせて:##################
次のものが入手できます:

##これは、私たちが提案した解決策によって得られた閉形式の解決策です。つまり、私たちの伝播メカニズムは、ノードのパーソナライズされた PageRank マトリックス上の特徴 H を伝播するのと同等になります。この伝播メカニズムでは、ノードは一定の確率で自分のノードに戻ることができるため、情報伝達の過程で自分の情報が失われることがなく、過剰平滑化の問題が回避されます。
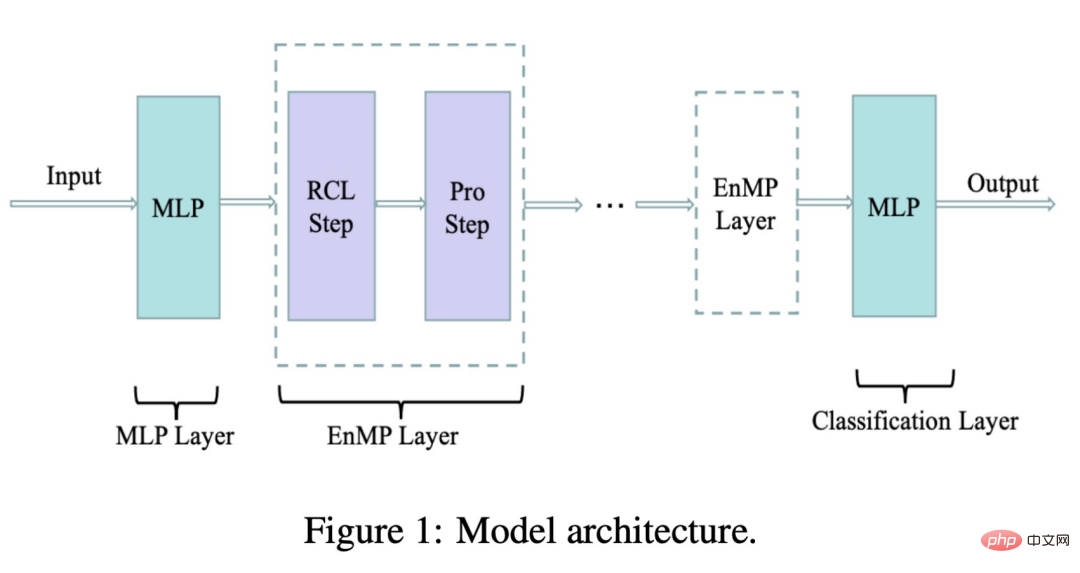
さらに、このモデルは、式からわかるように、各関係について学習可能な A のみを備えているため、過剰パラメータ化の現象も軽減します。係数 μr 、数値との比較前のエンコーダまたは重み行列 w#r のパラメータの大きさは、ほとんど無視できるほどです。次の図は、私たちが設計したモデル アーキテクチャです。

#ここで、RCL はパラメータ学習ステップです。 、Pro ステップは機能の伝播ステップです。これら 2 つのステップが一緒になってメッセージング層を形成します。では、追加のパラメーターを導入せずに、メッセージング レイヤーを DNN に統合するにはどうすればよいでしょうか?また、デカップリング設計のアイデアに従います: 最初に MLP を使用して入力特徴を抽出し、次に設計したメッセージ パッシング レイヤーの複数のレイヤーを通過します。複数のレイヤーを重ねても過度の平滑化が発生することはありません。最終的な転送結果は MLP によって処理されてノード分類が完了し、ダウンストリーム タスクに使用できます。式を使用して上記のプロセスを次のように表現します。

##f(X;W) は意味します。入力特徴は MLP を通じて抽出され、次の EnMP(K) は抽出結果が K レイヤ メッセージを通じて渡されることを意味します。 θ は分類された MLP を表します。 バックプロパゲーションでは、2 つの MLP のパラメータを更新するだけで済みますが、EnMP のパラメータはフォワードプロパゲーションプロセス中に学習されます。逆方向伝播プロセス中に EnMP のパラメータを更新する必要はありません。 さまざまなメカニズムのパラメーターを比較できます。EMR-GNN のパラメーターは主に前後 2 つの MLP から取得されていることがわかります。関係係数。層の数が 3 より大きい場合、EMR-GNN のパラメータの数は GCN のパラメータの数よりも少なく、他の異種グラフよりもさらに少ないことがわかります。
非常に少数のパラメータを使用して、EMR-GNN はさまざまなノードで次のように動作します。最高のレベルは分類タスクでも達成できます。

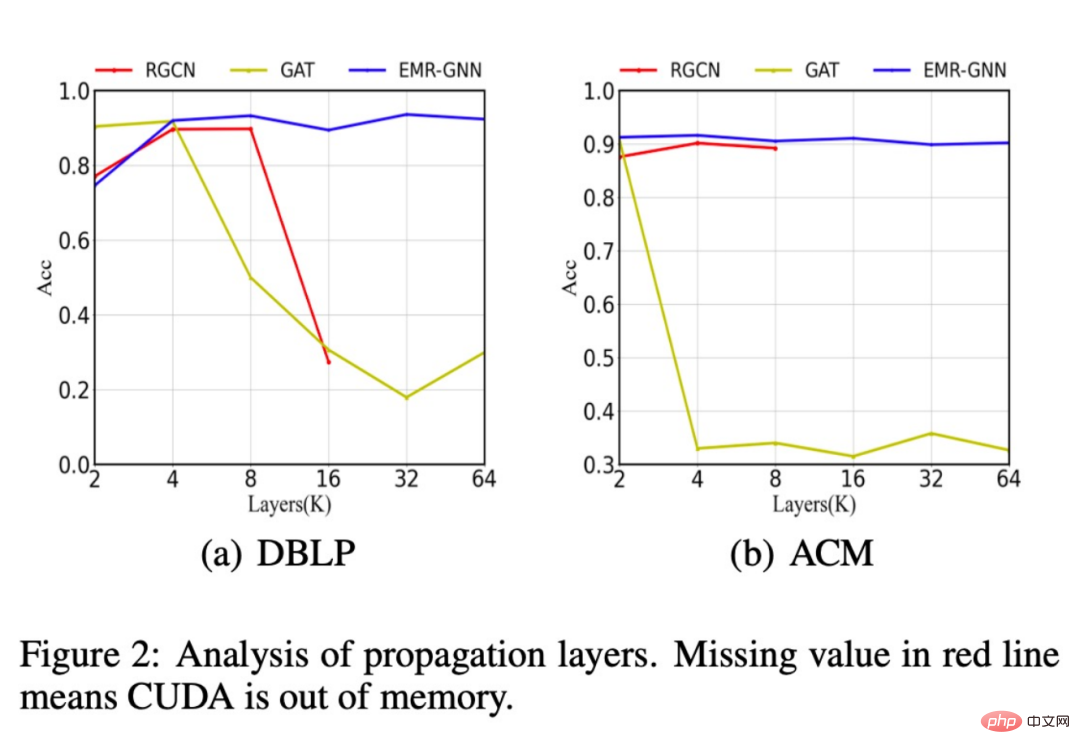
さらに、階層数が増加した後のさまざまなネットワーク構造の分類精度の変化も比較しました。下の図に示すように、階層数が 64 に増加すると、モデルは次のことが可能になります。高い精度を維持していますが、元の RGCN ではレイヤー数が 16 レイヤーを超えるとメモリ不足に陥り、パラメータが多すぎるためにこれ以上レイヤーを重ねることができなくなります。 GAT モデルのパフォーマンスは、過剰な平滑化により低下します。

さらに、EMR-GNN はデータ サイズが小さい場合にパフォーマンスが向上することもわかりました。サンプル全体の分類精度は達成できますが、RGCN は大幅に低下します。
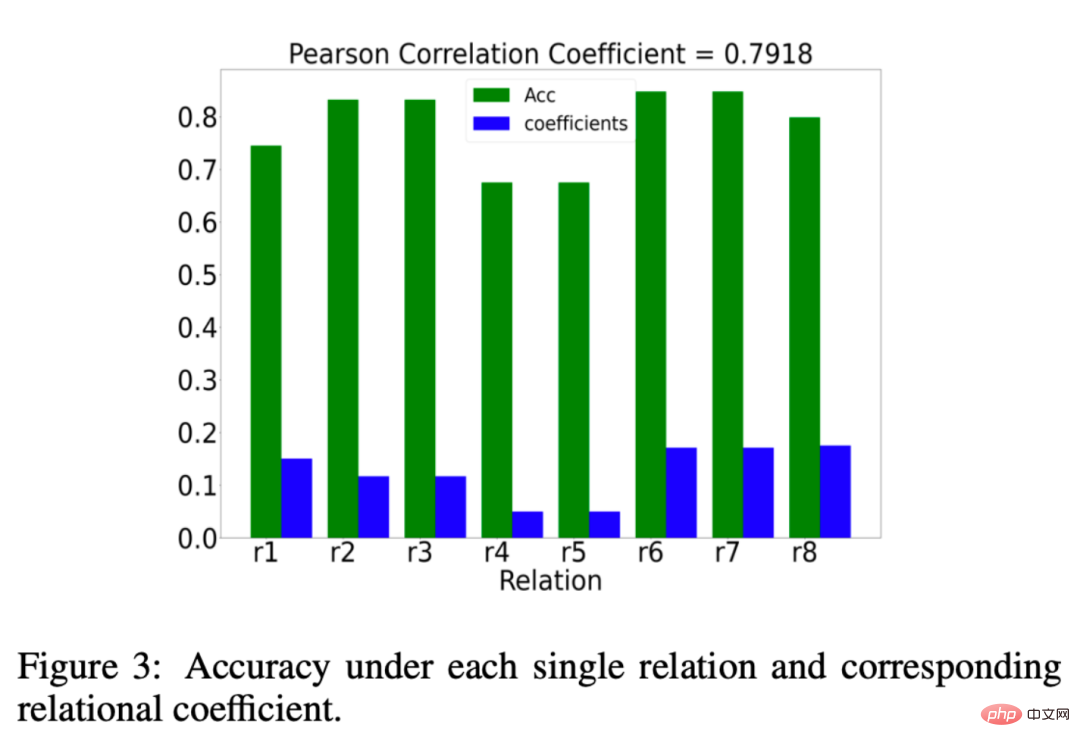
EMR-GNNで学習した関係係数μrが本当に意味があるのかについても分析しましたが、何が意味があるのでしょうか?関係係数 μr r が成立することを願っています。関係係数 重要な関係の重みを大きくし、重要でない関係の重みを減らします。分析の結果を以下の図に示します。

##緑のヒストグラムは、ある関係に基づく分類の効果 ある関係のもとで分類精度が高ければ、その関係は重要であると考えることができます。青い列は、EMR-GNN によって学習された関係係数を表します。青と緑の比較から、関係係数が関係の重要性を反映していることがわかります。
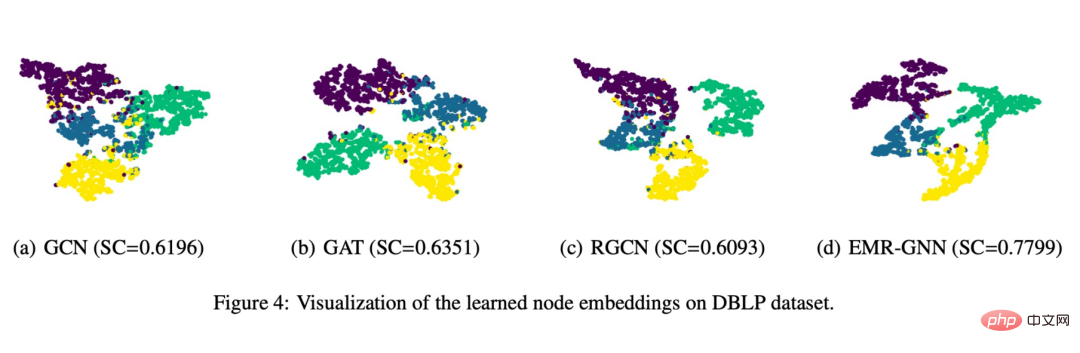
#最後に、以下に示すような視覚的な表示も作成しました。

EMR-GNN によってトレーニングされたノード エンベディングはノードの構造化情報を保持できることがわかります。これにより、同じタイプのノードをより凝集させ、異なるタイプのノードをより緊密にすることができます。分離すると、他のネットワークに比べてセグメント境界が明確になります。
4. 概要
##1. 統一された視点を使用して GNN
を理解します# ① この観点から、既存の GNN にどのような問題があるのかを簡単に確認できます。
② この統一された観点により、GNN の基本を再設計する方法が得られます。
#2. 目的関数の観点から新しいマルチリレーションシップ GNN の設計を試みます
## ①まず、統合最適化フレームワークを設計しました
## ② このような最適化フレームワークに基づいて、メッセージパッシングメカニズムを導き出しました
# ③ 少数のパラメータを持つこのメッセージ受け渡しメカニズムを MLP と組み合わせると、EMR-GNN
3 が得られます。EMR-GNN は、メリットは何ですか?
## ① 信頼できる最適化目標に依存しているため、得られる結果は信頼でき、その基礎となる原理は数学的に説明できます
② 既存の Relation GNN の過剰平滑化問題を解決できます
## ③ 過剰パラメータ化問題を解決します# ④ トレーニングが容易で、より少ないパラメータ量でより良い結果が得られます
5. Q&Aセッション
Q1: 関係係数の学習と注意メカニズムの間に違いはありますか?
A1: ここでの関係係数の学習は最適化フレームワークを通じて導き出される更新プロセスであり、注意はバックプロパゲーションに基づいて学習する必要があるプロセスであるため、最適化の観点からは両方が必要です。根本的な違いがあります。
#Q2: このモデルは大規模なデータセットにどの程度適用できますか?
A2: 付録でモデルの複雑さを分析しました。複雑さの点では RGCN と同等レベルですが、パラメーターの数は少なくなります。 RGCN よりも優れているため、私たちのモデルは大規模なデータセットにさらに適しています。
#Q3: このフレームワークにはエッジ情報を組み込むことができますか?
#A3: フィッティングタームまたは通常のタームに組み込むことができます。
#Q4: 数学の基礎はどこで学べばよいですか?
#A4: 一部は以前の研究に基づいており、最適化に関連する数学理論の他の部分もいくつかの古典的な最適化論文に基づいています。
#Q5: 関係図と異種図の違いは何ですか?
#A5: リレーションシップ グラフは異種グラフですが、通常、異種グラフとはノード タイプまたはエッジ タイプが 1 より大きいものと考えられます。関係図では、特に 1 より大きい関係カテゴリに注目します。後者には前者が含まれていることがわかります。
#Q6: ミニバッチ トレーニングはサポートできますか?
#A6: サポートされています。
Q7: GNN の将来の研究の方向性は、ヒューリスティックな設計よりも厳密で解釈可能な数学的導出に傾いているのでしょうか?
#A7: 私たち自身、厳密に解釈可能な数学的導出は信頼できる設計手法であると感じています。
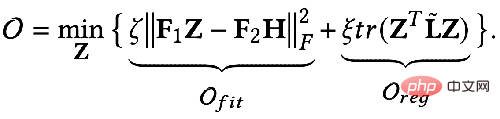
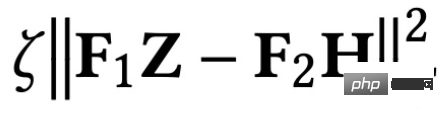
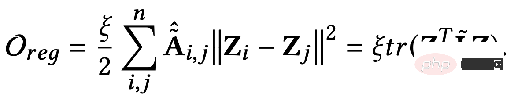
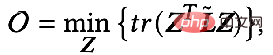
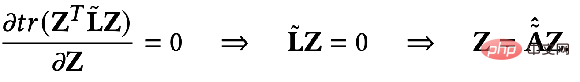
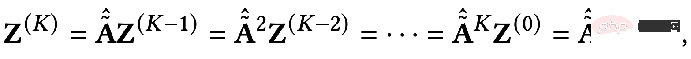
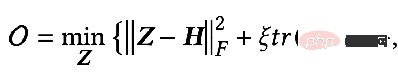
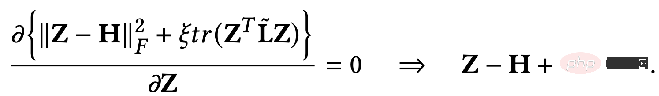
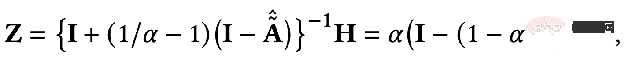
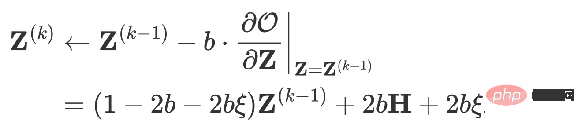
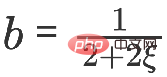
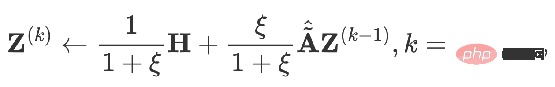
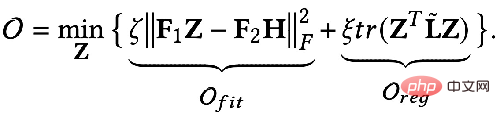
で正確な解決策を取得できます:
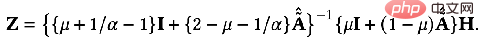
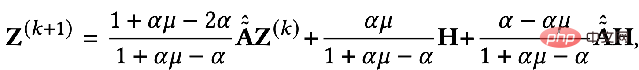
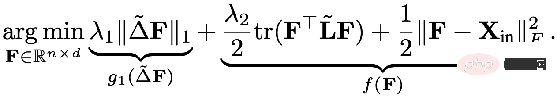
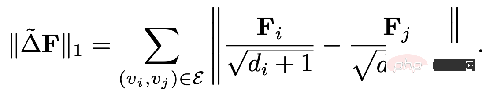
 #この種の多重関係図は、現実の世界で非常に広く普及しています。化学分子における複数の種類の分子結合。社会関係図における人々の間のさまざまな関係など。このようなグラフの場合、リレーショナル グラフ ニューラル ネットワークを使用してモデル化できます。主なアイデアは、N 個の関係を持つグラフを個別に集計して N 個の集計結果を取得し、その N 個の結果を集計することです。
#この種の多重関係図は、現実の世界で非常に広く普及しています。化学分子における複数の種類の分子結合。社会関係図における人々の間のさまざまな関係など。このようなグラフの場合、リレーショナル グラフ ニューラル ネットワークを使用してモデル化できます。主なアイデアは、N 個の関係を持つグラフを個別に集計して N 個の集計結果を取得し、その N 個の結果を集計することです。 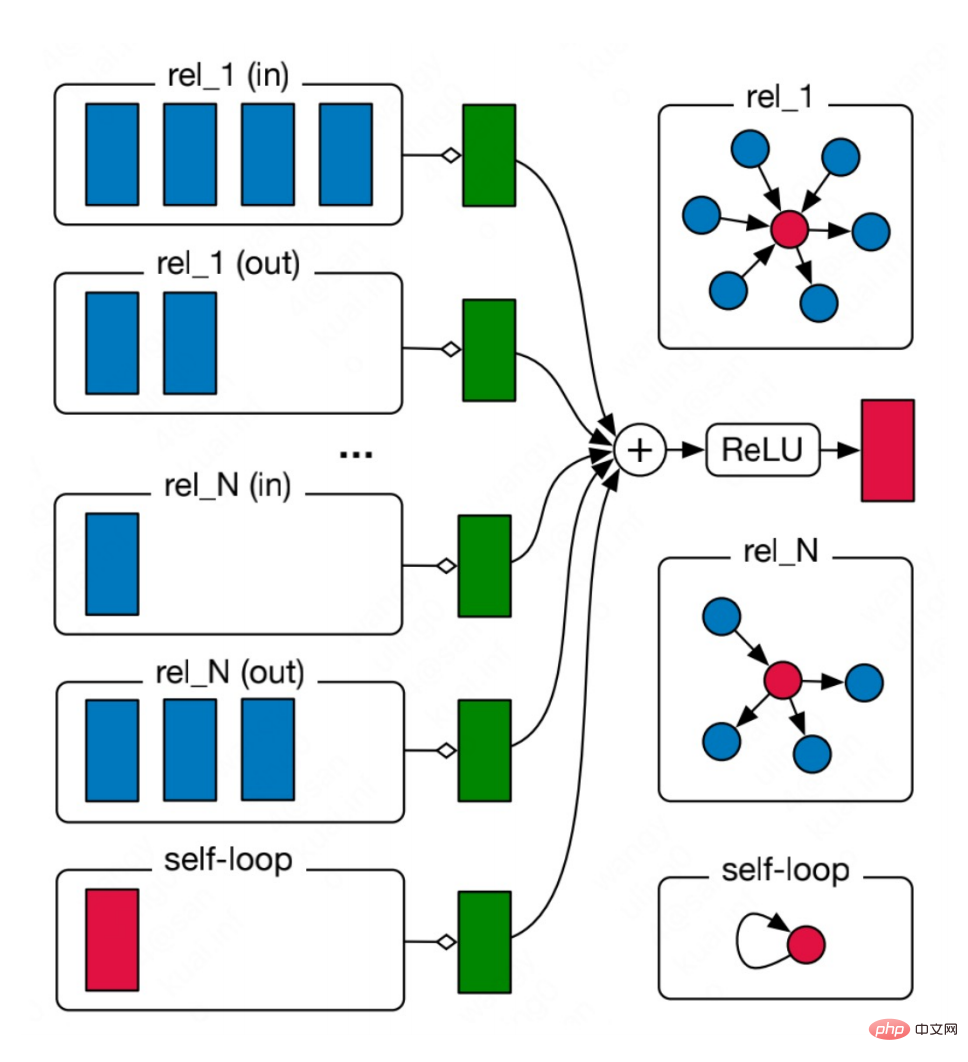 式で表すと次のようになります:
式で表すと次のようになります: 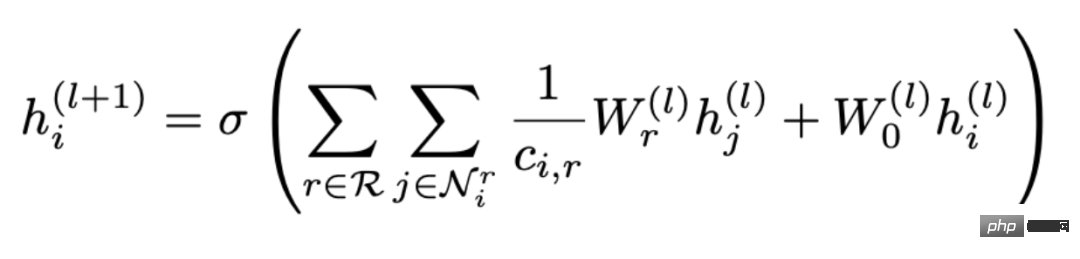 集計が 2 つのステップで実行されることがわかります。まず、すべての関係 R から関係 r を選択し、次に、次の関係を含む関係を見つけます。すべてのノード
集計が 2 つのステップで実行されることがわかります。まず、すべての関係 R から関係 r を選択し、次に、次の関係を含む関係を見つけます。すべてのノード 2、CompGCN
#過剰パラメータ化の問題を解決するために、CompGCN はベクトル化された関係エンコーダーを使用して N 関係行列を置き換えます:

エンコーダには、順方向、逆方向、自己ループの 3 方向の関係が含まれています。
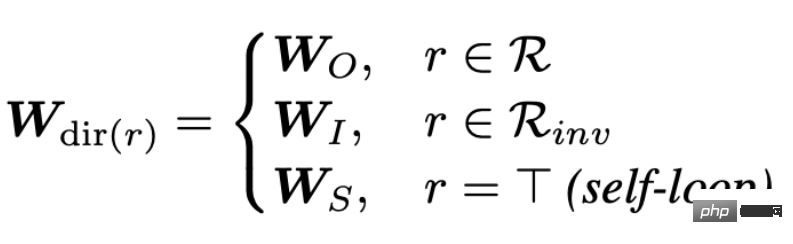
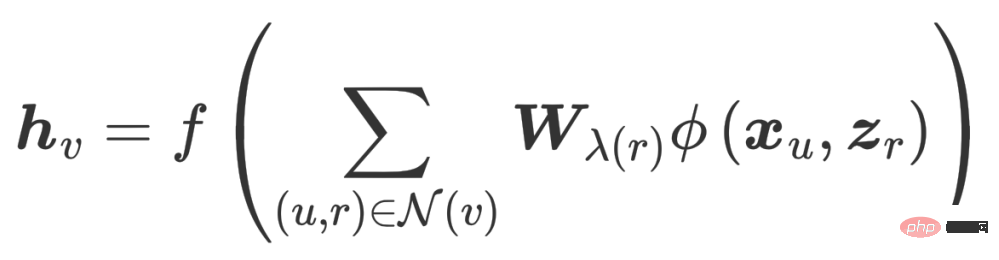
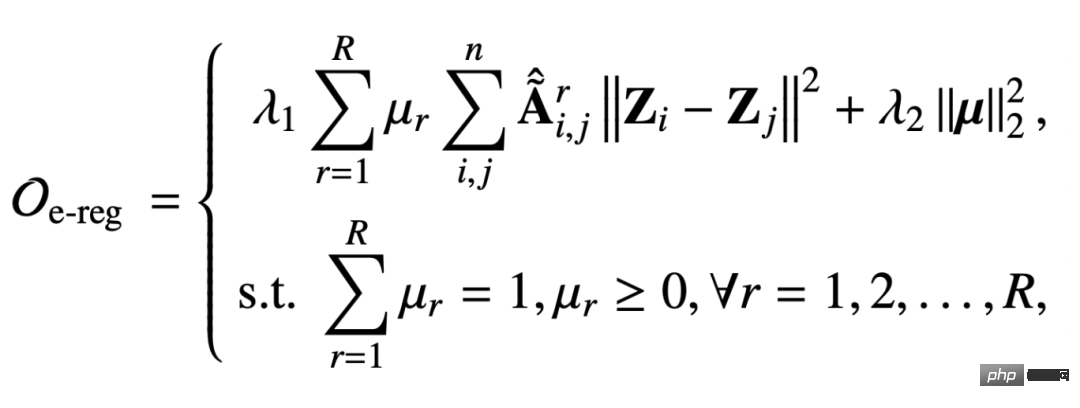
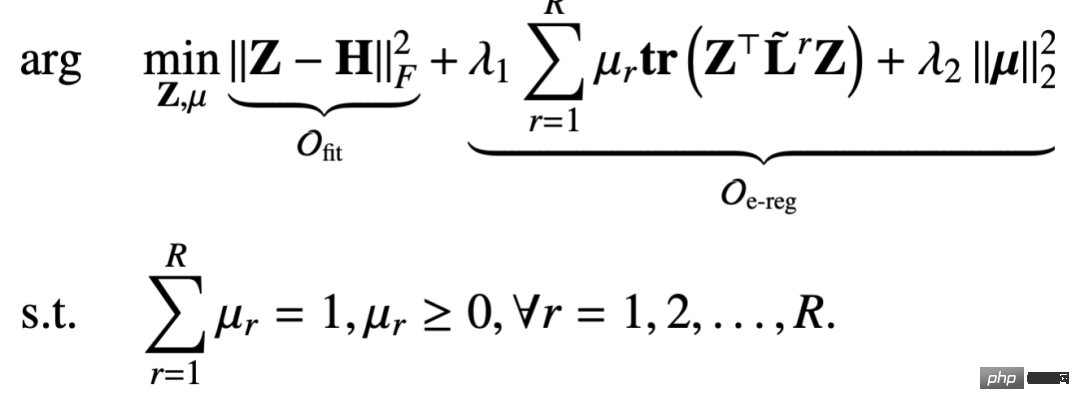
2. メッセージ受け渡しメカニズムの導出
ここでは、反復最適化戦略を採用します:
- ##最初にノード表現 Z を修正し、次にパラメータ μを最適化します。
- 次に、前の結果 μ に基づいてノードを最適化します。 iteration Represent Z
固定ノードが Z を表す場合、最適化目標全体は、制約付き目的関数のみに関連する目的関数に縮退します。
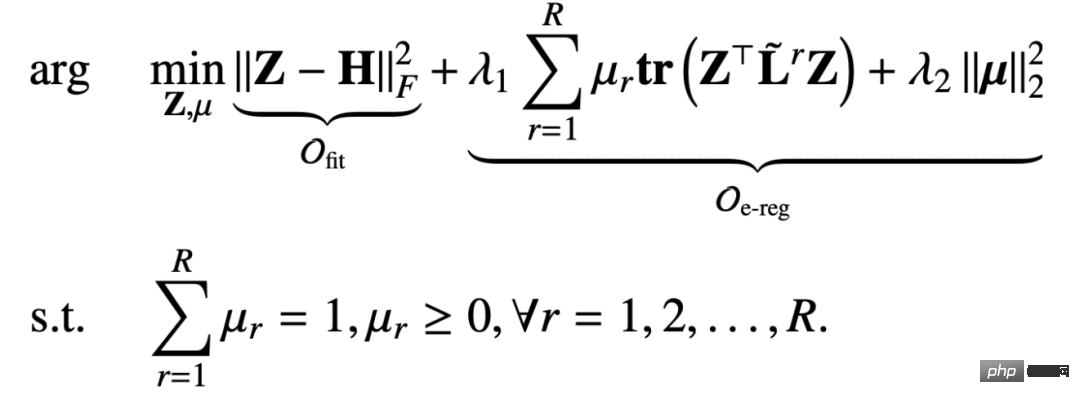

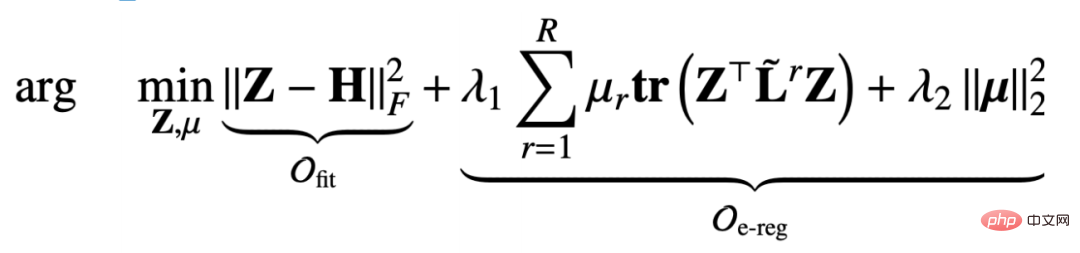
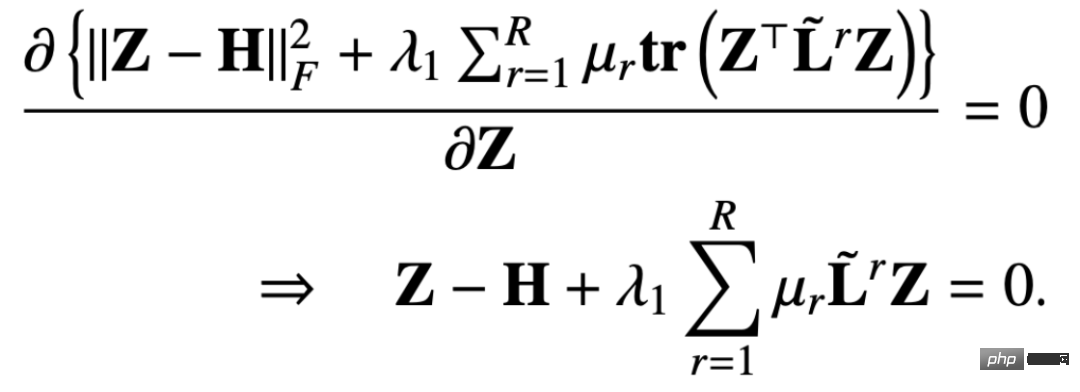
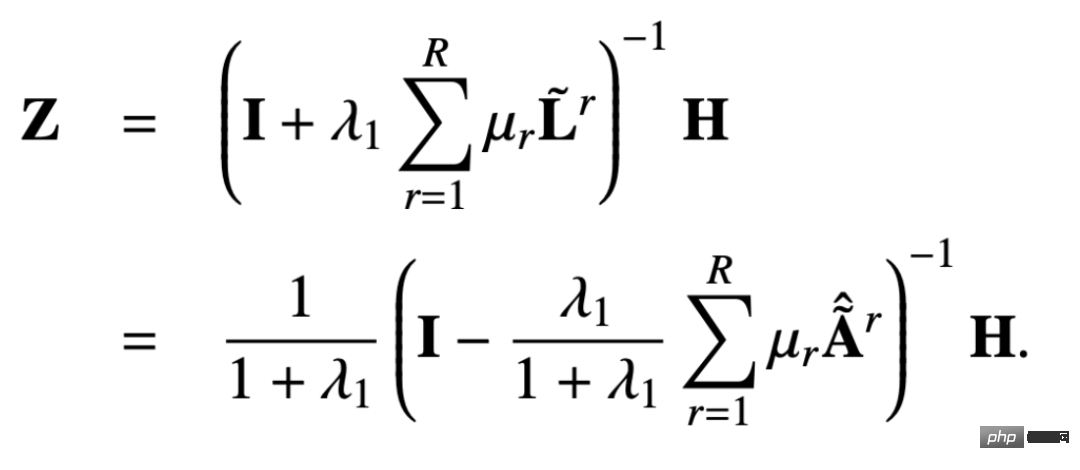
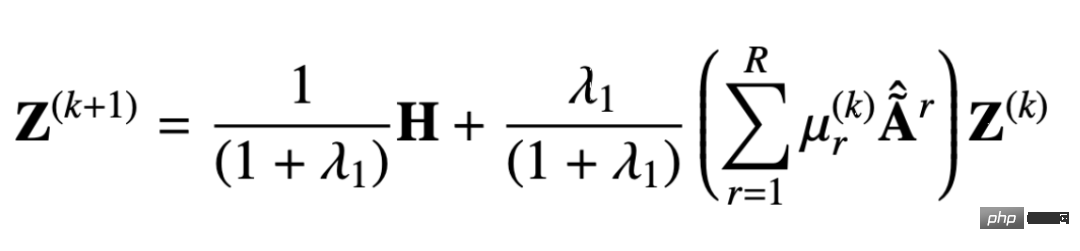
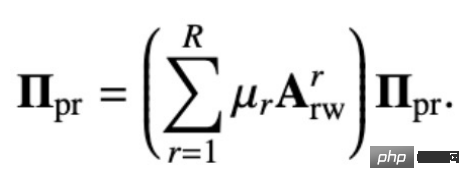
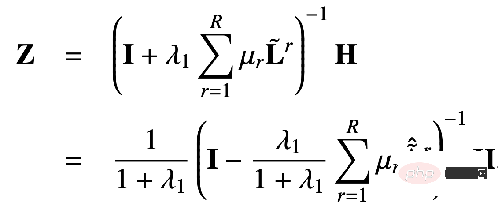
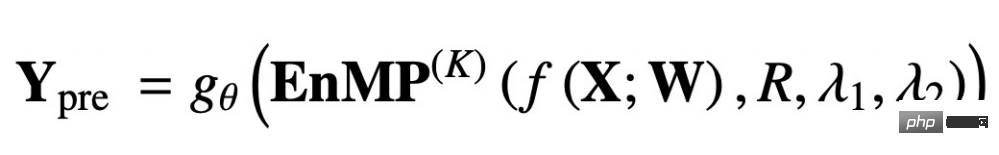
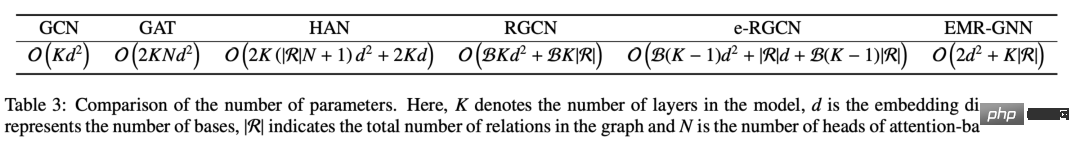
④ トレーニングが容易で、より少ないパラメータ量でより良い結果が得られます
5. Q&Aセッション
Q1: 関係係数の学習と注意メカニズムの間に違いはありますか?
A1: ここでの関係係数の学習は最適化フレームワークを通じて導き出される更新プロセスであり、注意はバックプロパゲーションに基づいて学習する必要があるプロセスであるため、最適化の観点からは両方が必要です。根本的な違いがあります。
#Q2: このモデルは大規模なデータセットにどの程度適用できますか?
A2: 付録でモデルの複雑さを分析しました。複雑さの点では RGCN と同等レベルですが、パラメーターの数は少なくなります。 RGCN よりも優れているため、私たちのモデルは大規模なデータセットにさらに適しています。
#Q3: このフレームワークにはエッジ情報を組み込むことができますか?
#A3: フィッティングタームまたは通常のタームに組み込むことができます。
#Q4: 数学の基礎はどこで学べばよいですか?
#A4: 一部は以前の研究に基づいており、最適化に関連する数学理論の他の部分もいくつかの古典的な最適化論文に基づいています。
#Q5: 関係図と異種図の違いは何ですか?
#A5: リレーションシップ グラフは異種グラフですが、通常、異種グラフとはノード タイプまたはエッジ タイプが 1 より大きいものと考えられます。関係図では、特に 1 より大きい関係カテゴリに注目します。後者には前者が含まれていることがわかります。
#Q6: ミニバッチ トレーニングはサポートできますか?
#A6: サポートされています。
Q7: GNN の将来の研究の方向性は、ヒューリスティックな設計よりも厳密で解釈可能な数学的導出に傾いているのでしょうか?#A7: 私たち自身、厳密に解釈可能な数学的導出は信頼できる設計手法であると感じています。
以上が統合されたマルチグラフ ニューラル ネットワークの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 1672
1672
 14
14
 1428
1428
 52
52
 1332
1332
 25
25
 1277
1277
 29
29
 1257
1257
 24
24
 AGNOフレームワークを使用してマルチモーダルAIエージェントを構築する方法は?
Apr 23, 2025 am 11:30 AM
AGNOフレームワークを使用してマルチモーダルAIエージェントを構築する方法は?
Apr 23, 2025 am 11:30 AM
エージェントAIに取り組んでいる間、開発者は速度、柔軟性、リソース効率の間のトレードオフをナビゲートすることがよくあります。私はエージェントAIフレームワークを探索していて、Agnoに出会いました(以前はPhi-でした。
 SQLに列を追加する方法は? - 分析Vidhya
Apr 17, 2025 am 11:43 AM
SQLに列を追加する方法は? - 分析Vidhya
Apr 17, 2025 am 11:43 AM
SQLの変更テーブルステートメント:データベースに列を動的に追加する データ管理では、SQLの適応性が重要です。 その場でデータベース構造を調整する必要がありますか? Alter Tableステートメントはあなたの解決策です。このガイドの詳細は、コルを追加します
 OpenaiはGPT-4.1でフォーカスをシフトし、コーディングとコスト効率を優先します
Apr 16, 2025 am 11:37 AM
OpenaiはGPT-4.1でフォーカスをシフトし、コーディングとコスト効率を優先します
Apr 16, 2025 am 11:37 AM
このリリースには、GPT-4.1、GPT-4.1 MINI、およびGPT-4.1 NANOの3つの異なるモデルが含まれており、大規模な言語モデルのランドスケープ内のタスク固有の最適化への動きを示しています。これらのモデルは、ようなユーザー向けインターフェイスをすぐに置き換えません
 Andrew Ngによる埋め込みモデルに関する新しいショートコース
Apr 15, 2025 am 11:32 AM
Andrew Ngによる埋め込みモデルに関する新しいショートコース
Apr 15, 2025 am 11:32 AM
埋め込みモデルのパワーのロックを解除する:Andrew Ngの新しいコースに深く飛び込む マシンがあなたの質問を完全に正確に理解し、応答する未来を想像してください。 これはサイエンスフィクションではありません。 AIの進歩のおかげで、それはRになりつつあります
 Rocketpyを使用したロケットの起動シミュレーションと分析-AnalyticsVidhya
Apr 19, 2025 am 11:12 AM
Rocketpyを使用したロケットの起動シミュレーションと分析-AnalyticsVidhya
Apr 19, 2025 am 11:12 AM
Rocketpy:A包括的なガイドでロケット発売をシミュレートします この記事では、強力なPythonライブラリであるRocketpyを使用して、高出力ロケット発売をシミュレートすることをガイドします。 ロケットコンポーネントの定義からシミュラの分析まで、すべてをカバーします
 Googleは、次の2025年にクラウドで最も包括的なエージェント戦略を発表します
Apr 15, 2025 am 11:14 AM
Googleは、次の2025年にクラウドで最も包括的なエージェント戦略を発表します
Apr 15, 2025 am 11:14 AM
GoogleのAI戦略の基礎としてのGemini Geminiは、GoogleのAIエージェント戦略の基礎であり、高度なマルチモーダル機能を活用して、テキスト、画像、オーディオ、ビデオ、コード全体で応答を処理および生成します。 DeepMによって開発されました
 3D自分で印刷できるオープンソースのヒューマノイドロボット:抱きしめる顔を購入する花粉ロボット工学
Apr 15, 2025 am 11:25 AM
3D自分で印刷できるオープンソースのヒューマノイドロボット:抱きしめる顔を購入する花粉ロボット工学
Apr 15, 2025 am 11:25 AM
「オープンソースロボットを世界に持ち込むために花粉ロボットを獲得していることを発表して非常にうれしいです」と、Facing FaceはXで述べました。
 DeepCoder-14B:O3-MINIおよびO1へのオープンソース競争
Apr 26, 2025 am 09:07 AM
DeepCoder-14B:O3-MINIおよびO1へのオープンソース競争
Apr 26, 2025 am 09:07 AM
AIコミュニティの重要な開発において、Agenticaと一緒にAIは、DeepCoder-14Bという名前のオープンソースAIコーディングモデルをリリースしました。 Openaiのようなクローズドソースの競合他社と同等のコード生成機能を提供する




