Java でトップ 10 の並べ替えアルゴリズムを実装する方法

ソートアルゴリズムの安定性:

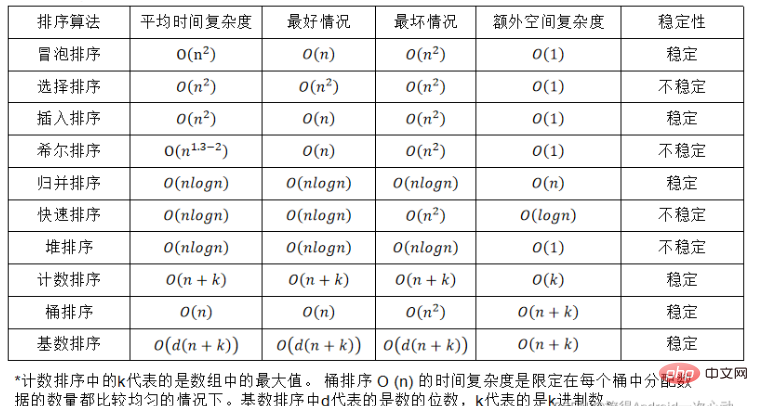
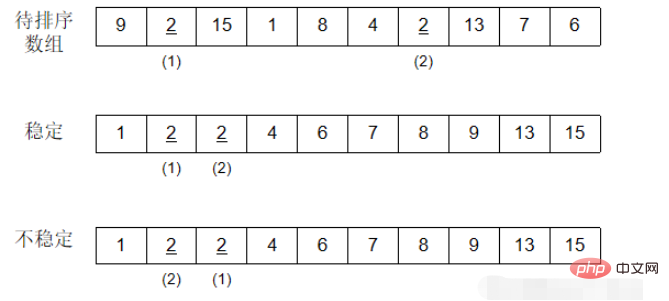
ソート対象のレコード列に同じキーワードを持つ複数のレコードが存在することを前提とし、ソート後のレコードが保証されるレコードの相対的な順序は変更されません。つまり、元のシーケンスでは、a[i]=a[j]、および a[i] が a[j] の前になります。ソート後は、a[i] であることが保証されます。 ] がまだ a[j] より前にある場合、この並べ替えアルゴリズムは安定と呼ばれ、それ以外の場合は不安定と呼ばれます。

1. 選択ソート

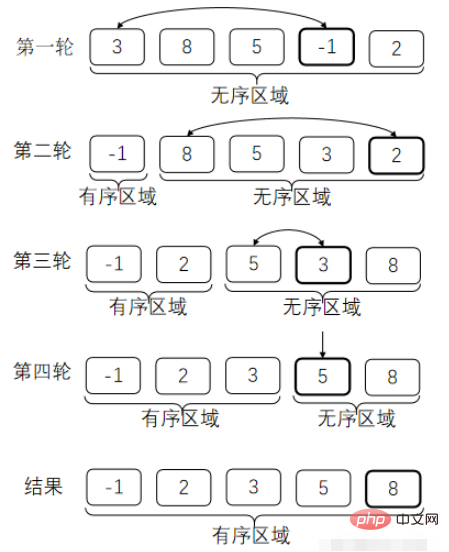
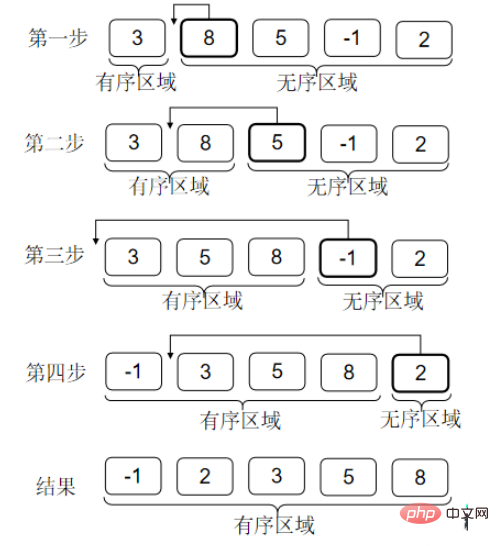
毎回、ソート対象の要素の中から最小の要素を選択し、1 番目、2 番目、...の順に配置します。 3番目...位置要素が交換されます。これにより、配列の先頭に順序付けられた領域が形成されます。スワップが実行されるたびに、順序付けされた領域の長さが 1 ずつ増加します。

public static void selectionSort(int[] arr){
    //细节一：这里可以是arr.length也可以是arr.length-1
    for (int i = 0; i < arr.length-1 ; i++) {
        int mini = i;
        for (int j = i+1; j < arr.length; j++) {
            //切换条件，决定升序还是降序
            if(arr[mini]>arr[j]) mini =j;
        }
        swap(arr,mini,i);
    }
}

2. バブルソート

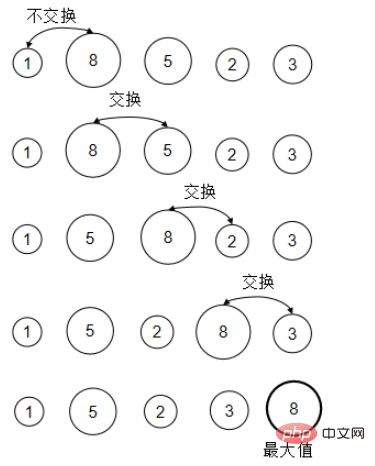
隣接する 2 つの数値を順番に比較します。順序が間違っている場合は、入れ替えます。この場合、それぞれの After比較のラウンドでは、最大の数値を入力すべき場所に入力できます。 （一番大きなバブルを一番上に持ってくるようなものです）

間違った順番の意味を説明します。昇順で並べ替えます。後の値は前の値以上である必要があります。そうでない場合は、それらを入れ替えます。

public static void bubbleSort(int[] arr){
    for (int i = 0; i < arr.length-1; i++) {
        //记录本次有没有进行交换的操作
        boolean flag = false;
        //保存在头就动头，保存在尾就动尾
        for(int j =0 ; j < arr.length-1-i ; j++){
            //升序降序选择地
            if(arr[j] > arr[j+1])
            {
                swap(arr,j,j+1);
                flag = true;
            }
        }
        //如果本次没有进行交换操作，表示数据已经有序
        if(!flag){break;} //程序结束
    }
}

3. インサーション ソート

インサーション ソートは、実際にはポーカーをプレイするときにカードを引くプロセスとして理解できます。カードは常に順番に並んでいます。カードがタッチされるたびに、カードは挿入されるべき場所に挿入されます。すべてのカードに触れると、すべてのカードが整います。

感想: 配列の前に順序付けられた領域ができているので、現在の数値を入れる位置を探すのに2進除算を使っています。挿入ソートの複雑さは O(nlogn) に最適化されていますか?

位置はログの複雑さで見つけることができます。重要なのは、配列を使用してデータを保存する場合、挿入中にデータを戻す複雑さは依然として O(n) であるということです。連結リストを使用する場合、位置を見つけて挿入するのは O(1) ですが、連結リストを 2 つに分割することはできません。

public static void insertSort(int[] arr){
        //从第二个数开始，把每个数依次插入到指定的位置
        for(int i = 1 ; i < arr.length ; i++)
        {
            int key = arr[i];
            int j = i-1;
            //大的后移操作
            while(j >= 0 && arr[j] > key)
            {
                arr[j+1] = arr[j];
                j--;
            }
            arr[j+1] = key;
        }
    }

4. ヒル ソート

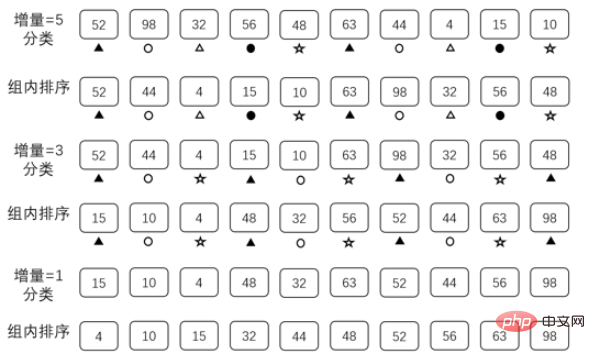
ヒル ソートは、1959 年に Donald Shell によって提案されたソート アルゴリズムです。ヒルソートでは、一連のデータを増分シーケンスとして準備する必要があります。

このデータ セットは、次の 3 つの条件を満たす必要があります:

1. データは降順に並べられています

2. データ内の最大値が以下であるソートする配列の長さ

3。データの最小値は 1 です。

配列が上記の要件を満たしている限り、インクリメンタル シーケンスとして使用できますが、インクリメンタル シーケンスが異なると並べ替えの効率に影響します。ここでは、

# 最適化を達成する理由を説明するために、増分シーケンスとして {5,3,1} を使用します。O(n) とO(n ^2) ギャップは大きくありません

public static void shellSort(int[] arr){
        //分块处理
        int gap = arr.length/2; //增量
        while(1<=gap)
        {
            //插入排序：只不过是与增量位交换
            for(int i = gap ; i < arr.length ; i++)
            {
                int key = arr[i];
                int j = i-gap;
                while(j >= 0 && arr[j] > key)
                {
                    arr[j+gap] = arr[j];
                    j-=gap;
                }
                arr[j+gap] = key;
            }
            gap = gap/2;
        }
    }

5。ヒープ ソート

は完全なバイナリ ツリーであり、大きなルート ヒープと小さなルート ヒープ

#の 2 つのタイプに分かれています。 ##can be O( 1) 最大/最小値を取得し、O(logn) の最大/最小値を削除し、O(logn) に要素を挿入します。

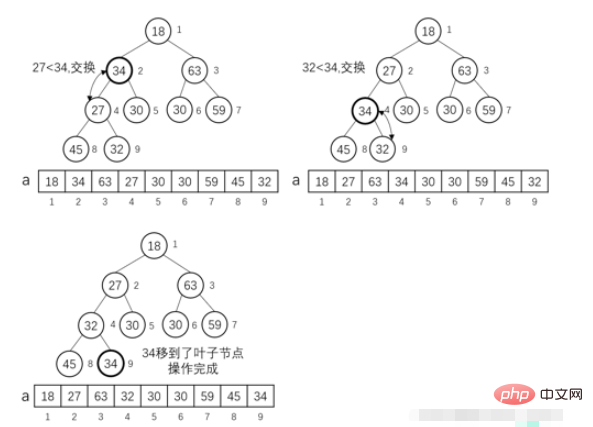
MIN-HEAPIFY (i) 操作:

完全なバイナリ ツリーを仮定します 特定のノード i の左のサブツリーと右のサブツリーの両方が、小さなルート ヒープのプロパティを満たします。ノード i の左の子が left_i で、右の子が left_i であると仮定します。ノード i は、rigℎt_i です。 a[i] が a[left_i] または a[rigℎt_i] より大きい場合、i ノードをルート ノードとするサブツリー全体は、小さなルート ヒープのプロパティを満たさないことになります。ここで、put i という操作を実行する必要があります。ルート ノードとして ルート ノードのサブツリーが小さなルート ヒープに調整されます。

//堆排序
    public static void heapSort(int[] arr){
        //开始调整的位置为最后一个叶子节点
        int start = (arr.length - 1)/2;
        //从最后一个叶子节点开始遍历，调整二叉树
        for (int i = start; i >= 0 ; i--){
            maxHeap(arr, arr.length, i);
        }
 
        for (int i = arr.length - 1; i > 0; i--){
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;
            maxHeap(arr, i, 0);
        }
    }
 
    //将二叉树调整为大顶堆
    public static void maxHeap(int[] arr, int size, int index){
        //建立左子节点
        int leftNode = 2 * index + 1;
        //建立右子节点
        int rightNode = 2 * index + 2;
 
        int maxNode = index;
        //左子节点的值大于根节点时调整
        if (leftNode < size && arr[leftNode] > arr[maxNode]){
            maxNode = leftNode;
        }
        //右子节点的值大于根节点时调整
        if (rightNode < size && arr[rightNode] > arr[maxNode]){
            maxNode = rightNode;
        }
        if (maxNode != index){
            int temp = arr[maxNode];
            arr[maxNode] = arr[index];
            arr[index] = temp;
            //交换之后可能会破坏原来的结构，需要再次调整
            //递归调用进行调整
            maxHeap(arr, size, maxNode);
        }
    }

私は大きなルート ヒープを使用しています。ソート プロセスは次のように要約されます: 最初に左のルート、次に右のルート (記述方法によって異なります) ->各ルートは上が下です。 (左、右、上、下)

6. マージ ソート

マージ ソートは分割統治法の典型的な応用例です。まず分割統治法について紹介しましょう。征服法とは、複雑な問題を 2 つ以上の同一または類似のサブ問題に分割し、その後、最終的なサブ問題が直接解決できるほど小さくなるまで、そのサブ問題をより小さなサブ問題に分割することです。サブ問題の解決策を組み合わせて、元の問題の解決策を取得します。

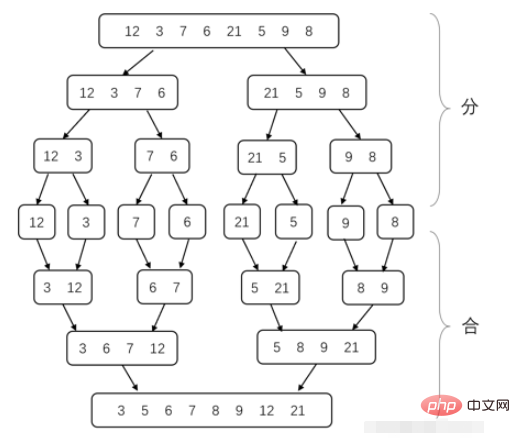
マージソート分解サブ問題のプロセスでは、配列の長さが 1 になるまで、毎回配列を 2 つの部分に分割します (数値が 1 つだけの配列が順序付けされているため)。 。次に、隣接する順序付き配列を 1 つの順序付き配列にマージします。それらがすべてまとめられるまで、配列全体がソートされます。ここで解決すべき問題は、2 つの順序付き配列を 1 つの順序付き配列にマージする方法です。実際には、毎回 2 つの配列の最小の 2 つの現在の要素を比較し、小さい方を選択します。

##1,3,42,5,7##2,5,7#1,3,44<5, 4 を取得し、配列 b のポインタを後方に移動します 1, 2、3、4##1、3、4配列 b には要素がありません。7 をとります1,2,3,4,5,7##

public static void mergeSort(int[] arr, int low, int high){
        int middle = (high + low)/2;
        if (low < high){
            //递归排序左边
            mergeSort(arr, low, middle);
            //递归排序右边
            mergeSort(arr, middle +1, high);
            //将递归排序好的左右两边合并
            merge(arr, low, middle, high);
        }
 
    }
 
    public static void merge(int[] arr, int low, int middle, int high){
        //存储归并后的临时数组
        int[] temp = new int[high - low + 1];
        int i = low;
        int j = middle + 1;
        //记录临时数组中存放数字的下标
        int index = 0;
        while (i <= middle && j <= high){
            if (arr[i] < arr[j]){
                temp[index] = arr[i];
                i++;
            } else {
                temp[index] = arr[j];
                j++;
            }
            index++;
        }
        //处理剩下的数据
        while (j <= high){
            temp[index] = arr[j];
            j++;
            index++;
        }
        while (i <= middle){
            temp[index] = arr[i];
            i++;
            index++;
        }
        //将临时数组中的数据放回原来的数组
        for (int k = 0; k < temp.length; ++k){
            arr[k + low] = temp[k];
        }
    }

七.快速排序

快速排序的工作原理是：从待排序数组中随便挑选一个数字作为基准数，把所有比它小的数字放在它的左边，所有比它大的数字放在它的右边。然后再对它左边的数组和右边的数组递归进行这样的操作。

全部操作完以后整个数组就是有序的了。 把所有比基准数小的数字放在它的左边，所有比基准数大的数字放在它的右边。这个操作，我们称为“划分”(Partition)。

	//快速排序
	public static void QuickSort1(int[] arr, int start, int end){
		int low = start, high = end;
		int temp;
		if(start < end){
		    int guard = arr[start];
			while(low != high){
				while(high > low && arr[high] >= guard) high--;
				while(low < high && arr[low] <= guard) low++;
				if(low < high){
					temp = arr[low];
					arr[low] = arr[high];
					arr[high] = temp;
				}
			}
			arr[start] = arr[low];
			arr[low] = guard;
			QuickSort1(arr, start, low-1);
			QuickSort1(arr, low+1, end);
		}
	}
	
	//快速排序改进版(填坑法)
	public static void QuickSort2(int[] arr, int start, int end){
		int low = start, high = end;
		if(start < end){
		while(low != high){
	    	int guard = arr[start];//哨兵元素
			while(high > low && arr[high] >= guard) high--;
			arr[low] = arr[high];
			while(low < high && arr[low] <= guard) low++;
			arr[high] = arr[low];
		}
		arr[low] = guard;
		QuickSort2(arr, start, low-1);
		QuickSort2(arr, low+1, end);
	}
}

八.鸽巢排序

计算一下每一个数出现了多少次。举一个例子，比如待排序的数据中1出现了2次，2出现了0次，3出现了3次，4出现了1次，那么排好序的结果就是{1.1.3.3.3.4}。

//鸽巢排序
    public static void PigeonholeSort(int[] arr){
        //获取最大值
        int k = 0;
        for (int i = 0; i < arr.length; i++) {
            k = Math.max(k,arr[i]);
        }
        //创建计数数组并且初始化为0
        int[] cnt = new int[k+10];
        for(int i = 0 ; i <= k ; i++) { cnt[i]=0; }
        for(int i = 0 ; i < arr.length ;i++) { cnt[arr[i]]++; }
        int j = 0;
        for(int i = 0 ; i <=k ; i++)
        {
            while(cnt[i]!=0)
            {
                arr[j]=i;
                j++;
                cnt[i]--;
            }
        }
    }

鸽巢排序其实算不上是真正意义上的排序算法，它的局限性很大。只能对纯整数数组进行排序，举个例子，如果我们需要按学生的成绩进行排序。是一个学生+分数的结构那就不能排序了。

九.计数排序

先考虑这样一个事情：如果对于待排序数据中的任意一个元素 a[i]，我们知道有 m 个元素比它小，那么我们是不是就可以知道排好序以后这个元素应该在哪个位置了呢？（这里先假设数据中没有相等的元素）。计数排序主要就是依赖这个原理来实现的。

比如待排序数据是{2,4,0,2,4} 先和鸽巢一样做一个cnt数组{1,0,2,0,2} 0,1,2,3,4

此时cnt[i]表示数据i出现了多少次，

然后对cnt数组做一个前缀和{1,1,3,3,5} ：0,1,2,3,4

此时cnt[i]表示数据中小于等于i的数字有多少个

配列 a	配列 b	説明	答えの配列
## 2,5 ,7	##1<2、1を取り、配列bのポインタを後方に移動します	1
1,3,4	2<3、2を取得、配列のポインタを後方に移動	1,2
1,3,4	##3<5、テイク 3、ポインタ配列 b 前に戻る	#1,2,3	##2,5,7
			##2、5、7
配列 b には要素がありません。5	#1,2,3,4,5	## を取ります #2,5,7	1,3,4

待排序数组	计数数组	说明	答案数组ans
2,4,0,2,4	1,1,3,3,5	初始状态	null,null,null,null,null,
2,4,0,2,4	1,1,3,3,5	cnt[4]=5，ans第5位赋值，cnt[4]-=1	null,null,null,null,4
2,4,0,2,4	1,1,3,3,4	cnt[2]=3，ans第3位赋值，cnt[2]-=1	null,null,2 null,4
2,4,0,2,4	1,1,2,3,4	cnt[0]=1，ans第1位赋值，cnt[0]-=1	0,null,2,null,4
2,4,0,2,4	0,1,2,3,4	cnt[4]=4，ans第4位赋值，cnt[4]-=1	0,null,2,4,4
2,4,0,2,4	0,1,2,3,3	cnt[2]=2，ans第2位赋值，cnt[2]-=1	0,2,2,4,4

十.基数排序

基数排序是通过不停的收集和分配来对数据进行排序的。

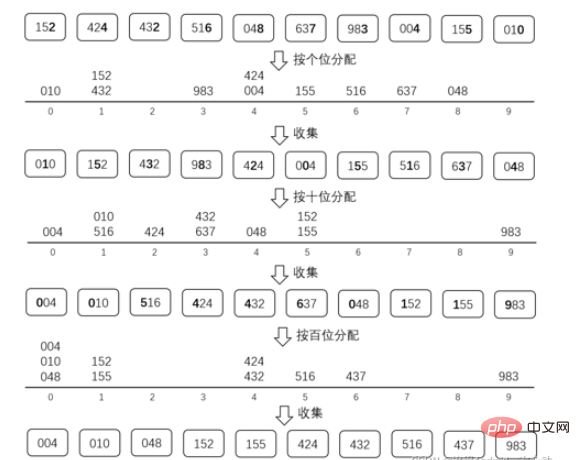
• 因为是10进制数，所以我们准备十个桶来存分配的数。

• 最大的数据是3位数，所以我们只需要进行3次收集和分配。

• 需要先从低位开始收集和分配（不可从高位开始排，如果从高位开始排的话，高位排好的顺序会在排低位的时候被打乱，有兴趣的话自己手写模拟一下试试就可以了）

• 在收集和分配的过程中，不要打乱已经排好的相对位置

比如按十位分配的时候，152和155这两个数的10位都是5，并且分配之前152在155的前面，那么收集的时候152还是要放在155之前的。

//基数排序
    public static void radixSort(int[] array) {
        //基数排序
        //首先确定排序的趟数;
        int max = array[0];
        for (int i = 1; i < array.length; i++) {
            if (array[i] > max) {
                max = array[i];
            }
        }
        int time = 0;
        //判断位数;
        while (max > 0) {
            max /= 10;
            time++;
        }
        //建立10个队列;
        List<ArrayList> queue = new ArrayList<ArrayList>();
        for (int i = 0; i < 10; i++) {
            ArrayList<Integer> queue1 = new ArrayList<Integer>();
            queue.add(queue1);
        }
        //进行time次分配和收集;
        for (int i = 0; i < time; i++) {
            //分配数组元素;
            for (int j = 0; j < array.length; j++) {
                //得到数字的第time+1位数;
                int x = array[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
                ArrayList<Integer> queue2 = queue.get(x);
                queue2.add(array[j]);
                queue.set(x, queue2);
            }
            int count = 0;//元素计数器;
            //收集队列元素;
            for (int k = 0; k < 10; k++) {
                while (queue.get(k).size() > 0) {
                    ArrayList<Integer> queue3 = queue.get(k);
                    array[count] = queue3.get(0);
                    queue3.remove(0);
                    count++;
                }
            }
 
        }
 
 
    }

以上がJava でトップ 10 の並べ替えアルゴリズムを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。