このタイプのテキストを解析するには、別の特定の文法規則が必要です。ここでは、文脈自由文法を表現できる文法規則バッカス正規形 (BNF) と拡張バッカス正規形 (EBNF) を紹介します。算術式のような小さなものから、ほぼすべてのプログラミング言語に相当する大きなものまで、文脈自由文法を使用して定義されます。
単純な算術演算式の場合、単語分割テクノロジを使用して、NUM NUM*NUM などの入力トークン ストリームに変換したと想定されます (詳細については、前のブログ投稿を参照してください)。単語分割法）。
これに基づいて、BNF ルールを次のように定義します:
expr ::= expr + term
| expr - term
| term
term ::= term * factor
| term / factor
| factor
factor ::= (expr)
| NUMもちろん、この方法は簡潔かつ明確ではありません。実際に使用するのは EBNF 形式です:
expr ::= term { (+|-) term }*
term ::= factor { (*|/) factor }*
factor ::= (expr)
| NUMBNF と EBNF の各規則 (::= の形式の式) は、置換とみなすことができます。つまり、左側の記号を右側の記号に置き換えることができます。解析プロセス中に BNF/EBNF を使用して入力テキストを文法規則と照合し、さまざまな置換や拡張を完了しようとします。 EBNF では、{...}* 内に配置されたルールはオプションであり、* はルールを 0 回以上繰り返すことができることを示します (正規表現と同様)。
次の図は、再帰降下パーサー (パーサー) と ENBF の「再帰」部分と「降下」部分の関係を明確に示しています。練習中、解析プロセス中にトークン ストリームを左から右にスキャンし、スキャン プロセス中にトークンを処理しますが、スタックすると構文エラーが生成されます。各文法ルールは関数またはメソッドに変換されます。たとえば、上記の ENBF ルールは次のメソッドに変換されます:
class ExpressionEvaluator():
...
def expr(self):
...
def term(self):
...
def factor(self):
...ルールに対応するメソッドを呼び出すプロセスで、次の記号が見つかった場合別のルールを使用して照合する必要がある場合は、別のルール メソッド (expr 内の term と term 内の因子を呼び出すなど) に「降順」します。これは、再帰降下の「降順」部分です。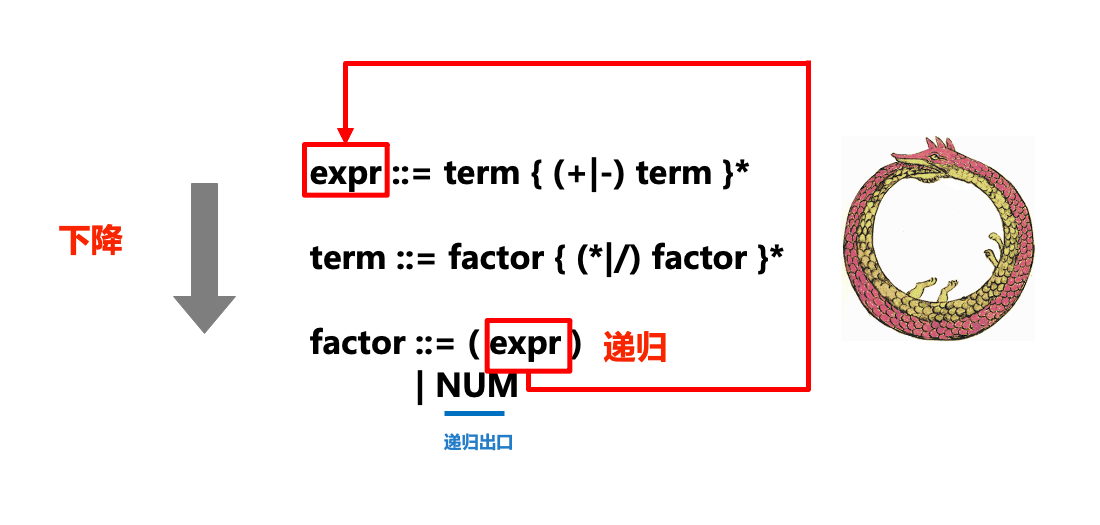 
expr ::= term { ( |-) term }*
など）については、while ループを介して実装します。 具体的なコードの実装を見てみましょう。まずは単語分割部分ですが、前回の記事を参考に単語分割ブログのコードを紹介しましょう。import re
import collections
# 定义匹配token的模式
NUM = r'(?P<NUM>\d+)' # \d表示匹配数字，+表示任意长度
PLUS = r'(?P<PLUS>\+)' # 注意转义
MINUS = r'(?P<MINUS>-)'
TIMES = r'(?P<TIMES>\*)' # 注意转义
DIVIDE = r'(?P<DIVIDE>/)'
LPAREN = r'(?P<LPAREN>\()' # 注意转义
RPAREN = r'(?P<RPAREN>\))' # 注意转义
WS = r'(?P<WS>\s+)' # 别忘记空格，\s表示空格，+表示任意长度
master_pat = re.compile(
'|'.join([NUM, PLUS, MINUS, TIMES, DIVIDE, LPAREN, RPAREN, WS]))
# Tokenizer
Token = collections.namedtuple('Token', ['type', 'value'])
def generate_tokens(text):
scanner = master_pat.scanner(text)
for m in iter(scanner.match, None):
tok = Token(m.lastgroup, m.group())
if tok.type != 'WS': # 过滤掉空格符
yield tok以下は式評価器の具体的な実装です: class ExpressionEvaluator():
""" 递归下降的Parser实现，每个语法规则都对应一个方法，
使用 ._accept()方法来测试并接受当前处理的token，不匹配不报错，
使用 ._except()方法来测试当前处理的token，并在不匹配的时候抛出语法错误
"""
def parse(self, text):
""" 对外调用的接口 """
self.tokens = generate_tokens(text)
self.tok, self.next_tok = None, None # 已匹配的最后一个token，下一个即将匹配的token
self._next() # 转到下一个token
return self.expr() # 开始递归
def _next(self):
""" 转到下一个token """
self.tok, self.next_tok = self.next_tok, next(self.tokens, None)
def _accept(self, tok_type):
""" 如果下一个token与tok_type匹配，则转到下一个token """
if self.next_tok and self.next_tok.type == tok_type:
self._next()
return True
else:
return False
def _except(self, tok_type):
""" 检查是否匹配，如果不匹配则抛出异常 """
if not self._accept(tok_type):
raise SyntaxError("Excepted"+tok_type)
# 接下来是语法规则，每个语法规则对应一个方法
def expr(self):
""" 对应规则： expression ::= term { ('+'|'-') term }* """
exprval = self.term() # 取第一项
while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.term()
if op == "PLUS":
exprval += right
elif op == "MINUS":
exprval -= right
return exprval
def term(self):
""" 对应规则： term ::= factor { ('*'|'/') factor }* """
termval = self.factor() # 取第一项
while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.factor()
if op == "TIMES":
termval *= right
elif op == "DIVIDE":
termval /= right
return termval
def factor(self):
""" 对应规则： factor ::= NUM | ( expr ) """
if self._accept("NUM"): # 递归出口
return int(self.tok.value)
elif self._accept("LPAREN"):
exprval = self.expr() # 继续递归下去求表达式值
self._except("RPAREN") # 别忘记检查是否有右括号，没有则抛出异常
return exprval
else:
raise SyntaxError("Expected NUMBER or LPAREN")e = ExpressionEvaluator()
print(e.parse("2"))
print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))
2
514
37。
入力したテキストが文法規則に準拠していない場合:print(e.parse("2 + (3 + * 4)"))ログイン後にコピー
、a SyntaxError 例外がスローされます: Expected NUMBER または LPAREN
要約すると、式評価アルゴリズムが正しく実行されていることがわかります。
2. 式ツリーの生成上記の式の結果が得られましたが、式の構造を分析して単純な式解析ツリーを生成したい場合はどうすればよいでしょうか?次に、上記のクラスのメソッドに特定の変更を加える必要があります:
class ExpressionTreeBuilder(ExpressionEvaluator):
def expr(self):
""" 对应规则： expression ::= term { ('+'|'-') term }* """
exprval = self.term() # 取第一项
while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.term()
if op == "PLUS":
exprval = ('+', exprval, right)
elif op == "MINUS":
exprval -= ('-', exprval, right)
return exprval
def term(self):
""" 对应规则： term ::= factor { ('*'|'/') factor }* """
termval = self.factor() # 取第一项
while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项，即运算符右值
right = self.factor()
if op == "TIMES":
termval = ('*', termval, right)
elif op == "DIVIDE":
termval = ('/', termval, right)
return termval
def factor(self):
""" 对应规则： factor ::= NUM | ( expr ) """
if self._accept("NUM"): # 递归出口
return int(self.tok.value) # 字符串转整形
elif self._accept("LPAREN"):
exprval = self.expr() # 继续递归下去求表达式值
self._except("RPAREN") # 别忘记检查是否有右括号，没有则抛出异常
return exprval
else:
raise SyntaxError("Expected NUMBER or LPAREN")print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))
print(e.parse('2+3+4'))(' ' , 2, 3)
(' ', 2, ('*', 3, 4))(' ', 2, ('*', (' ', 3, 4) ), 5))
(' ', (' ', 2, 3), 4)ファイルをチェックして確認してください。ただし、以下で説明するように、パーサーを自分で作成するには、さまざまな落とし穴や課題が伴います。 左再帰と演算子の優先順位のトラップGrammar
式ツリーが正しく生成されていることがわかります。
上記の例は非常に単純ですが、再帰降下パーサーを使用して非常に複雑なパーサーを実装することもできます。たとえば、Python コードは再帰降下パーサーを通じて解析されます。これに興味がある場合は、Python ソース コードの
左再帰
items ::= items ',' item
| itemdef items(self):
itemsval = self.items() # 取第一项，然而此处会无穷递归！
if itemsval and self._accept(','):
itemsval.append(self.item())
else:
itemsval = [self.item()]expr ::= factor { ('+'|'-'|'*'|'/') factor }*
factor ::= '(' expr ')'
| NUMPYTHON Copy full screenこの構文は技術的には実装できますが、計算順序の規則に従っていないため、「」が発生します。 3 4* 5" は、予想どおり 23 ではなく 35 と評価されます。したがって、計算結果の正確性を保証するには、個別の expr ルールと term ルールが必要です。 以上がPython で再帰降下パーサーを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
![[Web フロントエンド] Node.js クイック スタート](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
