
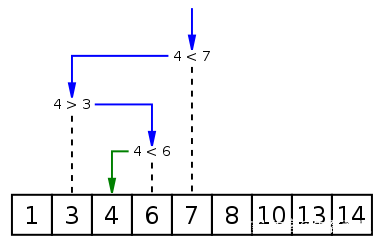
二分検索は、順序付けされた順序で特定の値を検索する方法です。配列要素の検索アルゴリズム。検索処理は配列の中央の要素から開始され、中央の要素が見つかった場合は検索処理を終了し、特定の要素が中央の要素より大きいか小さい場合は半分の要素を検索します。配列の中央の要素より大きいか小さいかを比較し、最初と同様に中央の要素から比較を開始します。特定のステップで配列が空の場合、それは見つからないことを意味します。この検索アルゴリズムでは、比較するたびに検索範囲が半分に減ります。
# 返回 x 在 arr 中的索引,如果不存在返回 -1
def binarySearch (arr, l, r, x):
# 基本判断
if r >= l:
mid = int(l + (r - l)/2)
# 元素整好的中间位置
if arr[mid] == x:
return mid
# 元素小于中间位置的元素,只需要再比较左边的元素
elif arr[mid] > x:
return binarySearch(arr, l, mid-1, x)
# 元素大于中间位置的元素,只需要再比较右边的元素
else:
return binarySearch(arr, mid+1, r, x)
else:
# 不存在
return -1
# 测试数组
arr = [ 2, 3, 4, 10, 40]
x = int(input('请输入元素:'))
# 函数调用
result = binarySearch(arr, 0, len(arr)-1, x)
if result != -1:
print("元素在数组中的索引为 %d" % result)
else:
print("元素不在数组中")実行結果:
要素を入力してください: 4
要素のインデックス配列は 2 です
要素を入力してください: 5
要素は配列内にありません
線形検索: 探している特定の値が見つかるまで、配列内の各要素を特定の順序でチェックすることを指します。
def search(arr, n, x):
for i in range (0, n):
if (arr[i] == x):
return i
return -1
# 在数组 arr 中查找字符 D
arr = [ 'A', 'B', 'C', 'D', 'E' ]
x = input("请输入要查找的元素:")
n = len(arr)
result = search(arr, n, x)
if(result == -1):
print("元素不在数组中")
else:
print("元素在数组中的索引为", result)実行結果:
検索する要素を入力してください: 配列内の A
です
要素のインデックスは 0
#並べ替え検索したい要素を入力してください: a
要素は配列内にありません
は、シンプルで直感的なソート アルゴリズムです。これは、順序付けされたシーケンスを構築することで機能し、並べ替えられていないデータの場合は、並べ替えられたシーケンス内で後ろから前にスキャンし、対応する位置を見つけて挿入します。
def insertionSort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i-1
while j >= 0 and key < arr[j]:
arr[j+1] = arr[j]
j -= 1
arr[j+1] = key
arr = [12, 11, 13, 5, 6, 7, 9, 9, 17]
insertionSort(arr)
print("排序后的数组:")
print(arr)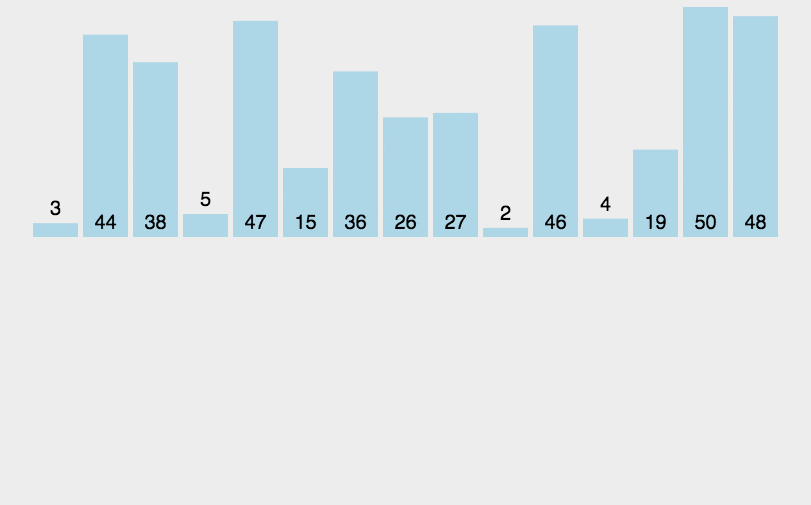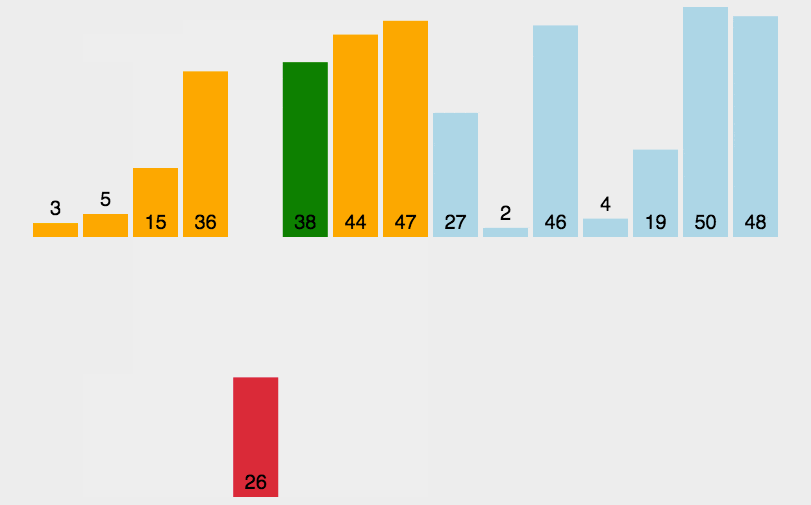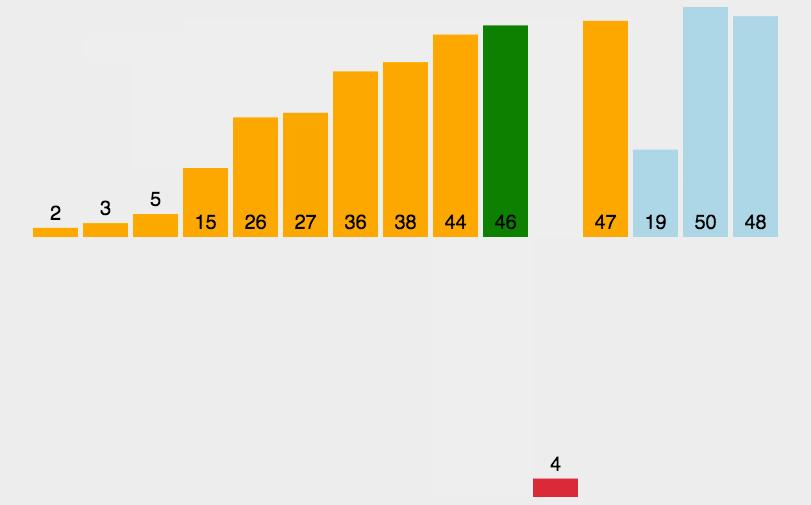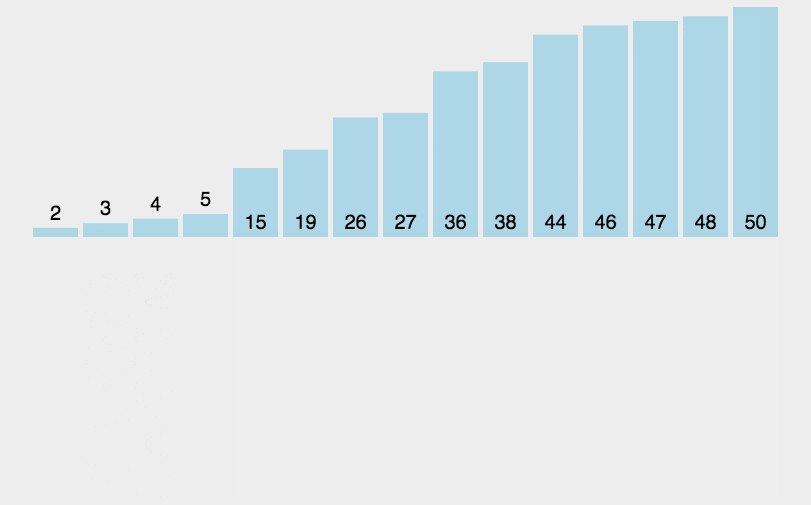 実行結果:
実行結果: ソートされた配列:
[5, 6, 7, 9 , 9 、11、12、13、17]もちろん、このように書くこともできます。そのほうがより簡潔です
list1 = [12, 11, 13, 5, 6, 7, 9, 9, 17]
for i in range(len(list1)-1, 0, -1):
for j in range(0, i):
if list1[i] < list1[j]:
list1[i], list1[j] = list1[j], list1[i]
print(list1)クイックソート
分割統治戦略を使用して、シーケンス (リスト) を 2 つのサブシーケンス (小さい方と大きい方) に分割し、その 2 つのサブシーケンスを再帰的に並べ替えます。
手順は次のとおりです:シーケンスから「base」と呼ばれる要素を選択します。 " (ピボット);
シーケンスを並べ替えます。ベースライン値より小さい要素はすべてベースラインの前に配置され、ベースライン値より大きい要素はすべて配置されます。ベースライン値は、ベースラインの前、ベースの後ろに配置されます (ベース値に等しい数値はどちらの側にも配置できます)。この分割が完了すると、基準値のソートが完了します。
基準値未満の要素の部分列を再帰的に結合します基本値要素のサブシーケンス順序付けより大きい。
ベンチマーク値の具体的な選択方法はいくつかありますが、この選択方法がソートの時間パフォーマンスに決定的な影響を与えます。
def partition(arr, low, high):
i = (low-1) # 最小元素索引
pivot = arr[high]
for j in range(low, high):
# 当前元素小于或等于 pivot
if arr[j] <= pivot:
i = i+1
arr[i], arr[j] = arr[j], arr[i]
arr[i+1], arr[high] = arr[high], arr[i+1]
return (i+1)
# arr[] --> 排序数组
# low --> 起始索引
# high --> 结束索引
# 快速排序函数
def quickSort(arr, low, high):
if low < high:
pi = partition(arr, low, high)
quickSort(arr, low, pi-1)
quickSort(arr, pi+1, high)
return arr
arr = [10, 7, 8, 9, 1, 5]
n = len(arr)
print("排序后的数组:")
print(quickSort(arr, 0, n-1))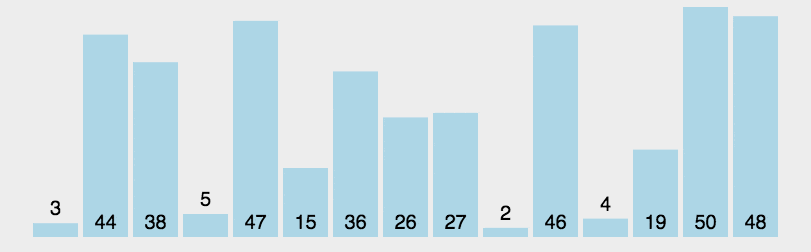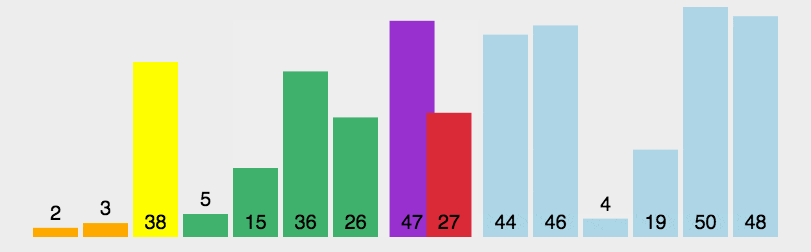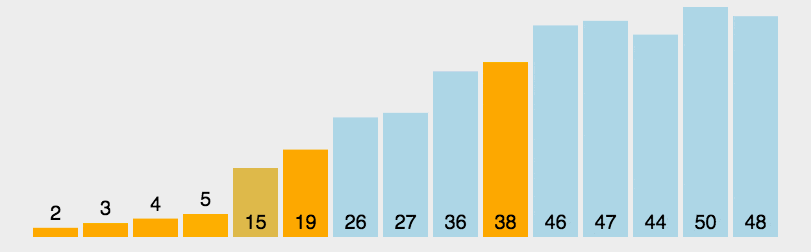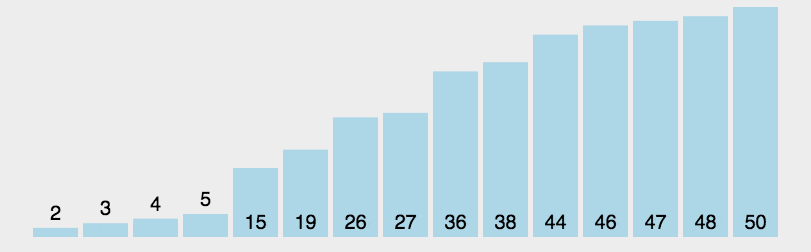 実行結果:
実行結果: ソートされた配列:
[1, 5, 7, 8 , 9 , 10]選択ソート (選択ソート):選択ソート
は、シンプルで直感的な並べ替えアルゴリズムです。仕組みは次のとおりです。 まず、ソートされていないシーケンスの中で最も小さい (大きい) 要素を見つけて、ソートされたシーケンスの開始位置に格納し、その後、引き続きソートされていない残りの要素から最も小さい (大きい) 要素を見つけて配置します。ソートされたシーケンス。シーケンスの終わり。すべての要素がソートされるまで続きます。
A = [64, 25, 12, 22, 11]
for i in range(len(A)):
min_idx = i
for j in range(i+1, len(A)):
if A[min_idx] > A[j]:
min_idx = j
A[i], A[min_idx] = A[min_idx], A[i]
print("排序后的数组:")
print(A)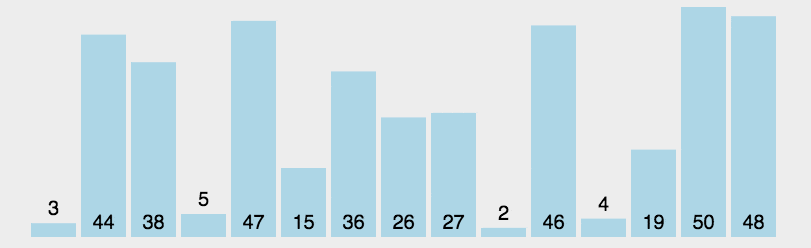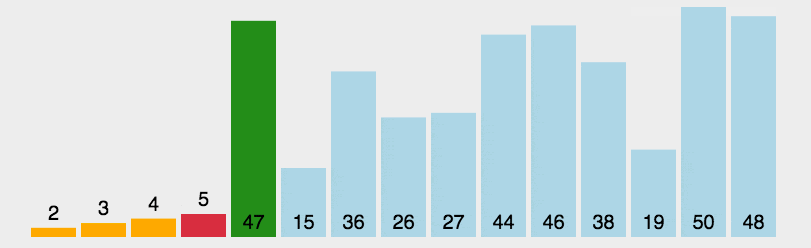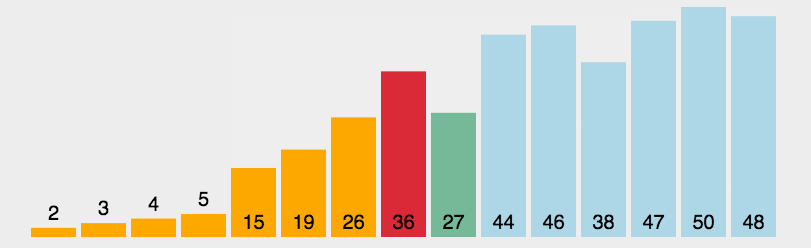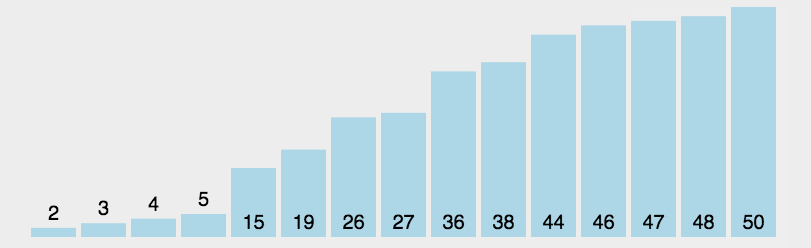 実行結果:
実行結果: ソートされた配列:
[11, 12, 22, 25 , 64 ]バブル ソート:バブル ソート
も、シンプルで直感的な並べ替えアルゴリズムです。ソート対象のシーケンスを繰り返し調べて、一度に 2 つの要素を比較し、順序が間違っている場合はそれらを交換します。配列を訪問する作業は、それ以上の交換が必要なくなるまで繰り返されます。これは、配列がソートされたことを意味します。このアルゴリズムの名前は、小さい要素がスワッピングによって配列の先頭にゆっくりと「浮動」するという事実に由来しています。
def bubbleSort(arr):
n = len(arr)
# 遍历所有数组元素
for i in range(n):
# Last i elements are already in place
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
return arr
arr = [64, 34, 25, 12, 22, 11, 90]
print("排序后的数组:")
print(bubbleSort(arr))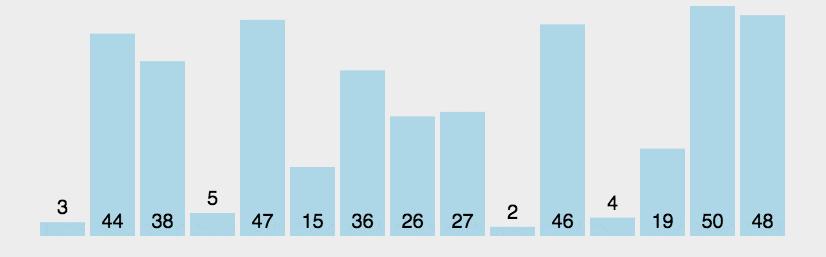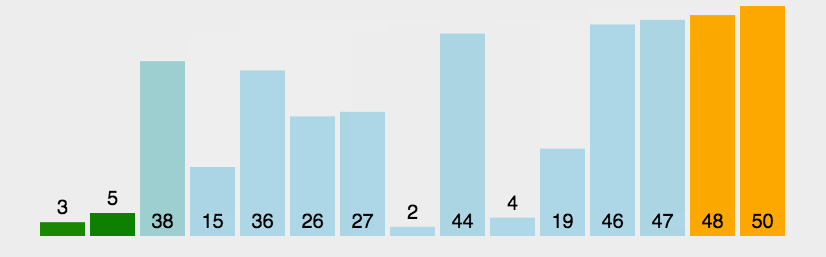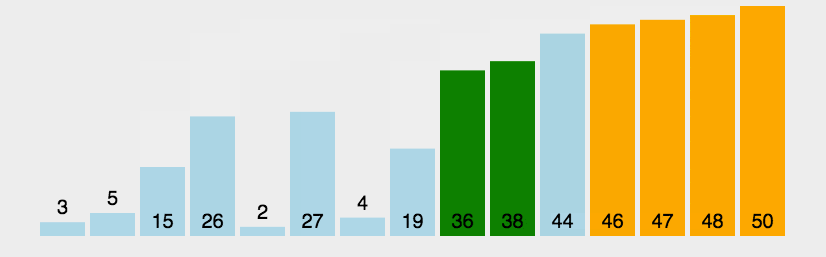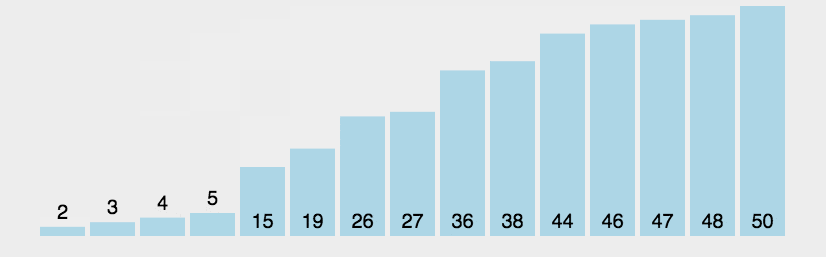 実行結果:
実行結果: ソートされた配列:
[11, 12, 22, 25 , 34 、64、90]
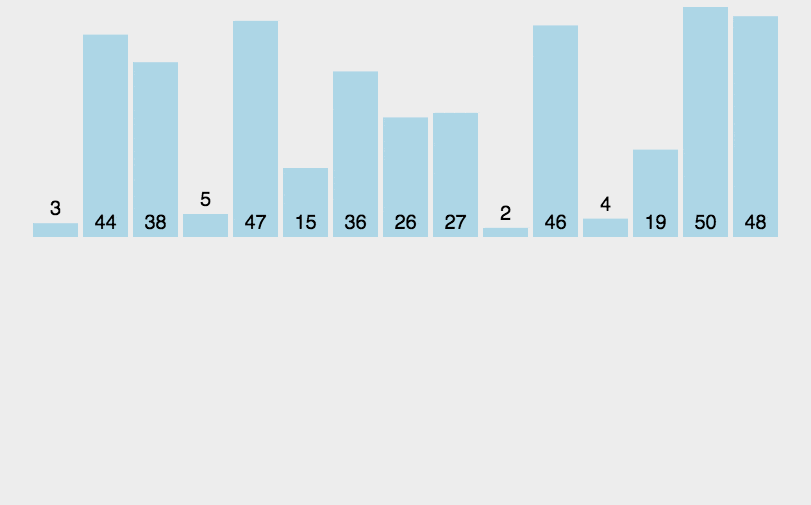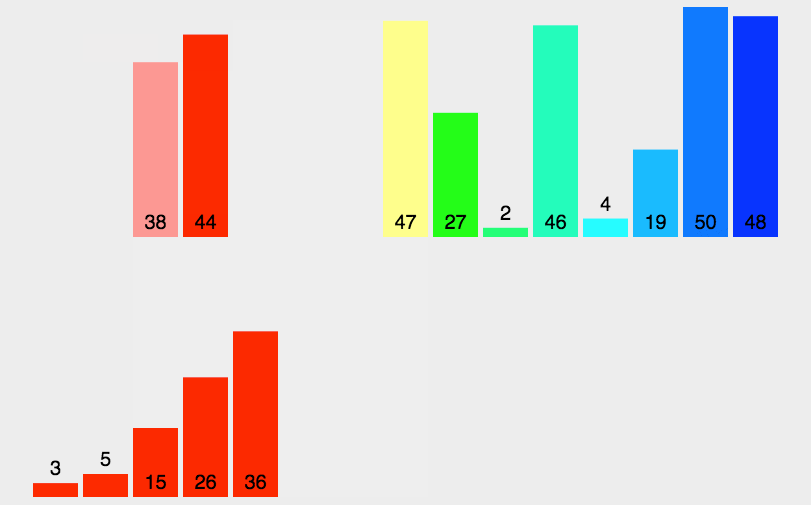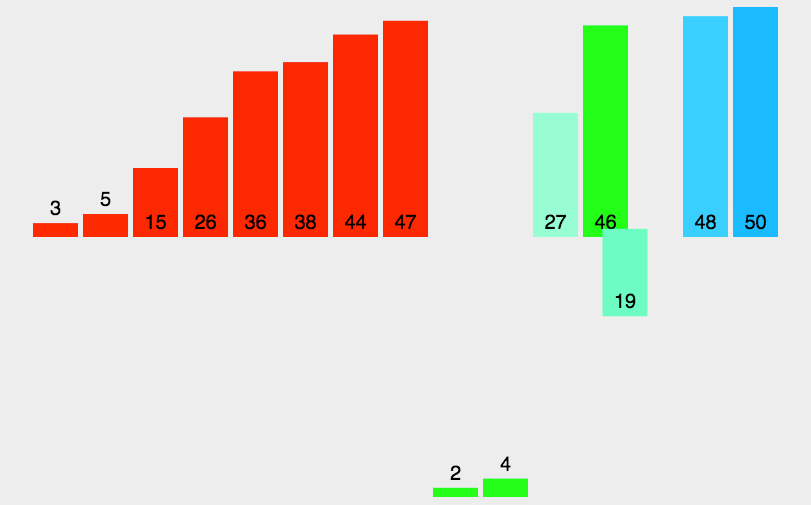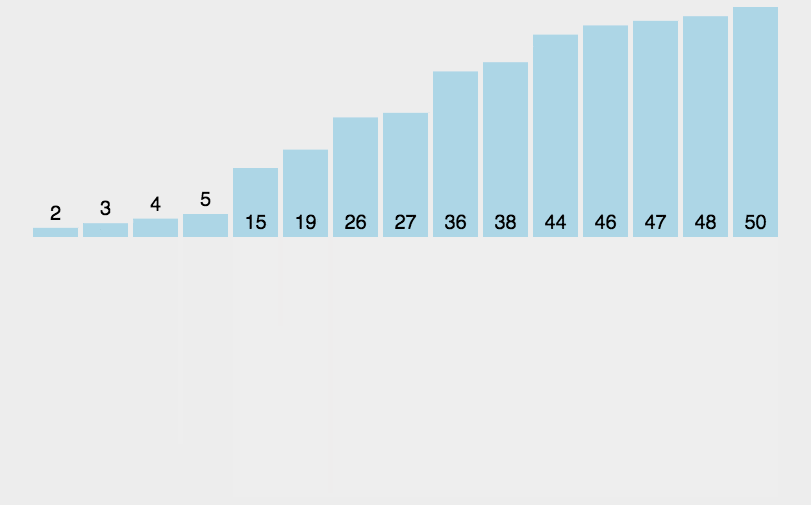
归并排序(Merge sort,或mergesort):,是创建在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
分治法:
分割:递归地把当前序列平均分割成两半。
集成:在保持元素顺序的同时将上一步得到的子序列集成到一起(归并)。
def merge(arr, l, m, r):
n1 = m - l + 1
n2 = r - m
# 创建临时数组
L = [0] * (n1)
R = [0] * (n2)
# 拷贝数据到临时数组 arrays L[] 和 R[]
for i in range(0, n1):
L[i] = arr[l + i]
for j in range(0, n2):
R[j] = arr[m + 1 + j]
# 归并临时数组到 arr[l..r]
i = 0 # 初始化第一个子数组的索引
j = 0 # 初始化第二个子数组的索引
k = l # 初始归并子数组的索引
while i < n1 and j < n2:
if L[i] <= R[j]:
arr[k] = L[i]
i += 1
else:
arr[k] = R[j]
j += 1
k += 1
# 拷贝 L[] 的保留元素
while i < n1:
arr[k] = L[i]
i += 1
k += 1
# 拷贝 R[] 的保留元素
while j < n2:
arr[k] = R[j]
j += 1
k += 1
def mergeSort(arr, l, r):
if l < r:
m = int((l+(r-1))/2)
mergeSort(arr, l, m)
mergeSort(arr, m+1, r)
merge(arr, l, m, r)
return arr
print ("给定的数组")
arr = [12, 11, 13, 5, 6, 7, 13]
print(arr)
n = len(arr)
mergeSort(arr, 0, n-1)
print("排序后的数组")
print(arr)运行结果:
给定的数组
[12, 11, 13, 5, 6, 7, 13]
排序后的数组
[5, 6, 7, 11, 12, 13, 13]
堆排序(Heapsort):是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。

def heapify(arr, n, i):
largest = i
l = 2 * i + 1 # left = 2*i + 1
r = 2 * i + 2 # right = 2*i + 2
if l < n and arr[i] < arr[l]:
largest = l
if r < n and arr[largest] < arr[r]:
largest = r
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i] # 交换
def heapSort(arr):
n = len(arr)
# Build a maxheap.
for i in range(n, -1, -1):
heapify(arr, n, i)
# 一个个交换元素
for i in range(n-1, 0, -1):
arr[i], arr[0] = arr[0], arr[i] # 交换
heapify(arr, i, 0)
return arr
arr = [12, 11, 13, 5, 6, 7, 13, 18]
heapSort(arr)
print("排序后的数组")
print(heapSort(arr))运行结果:
排序后的数组
[5, 6, 7, 12, 11, 13, 13, 18]
计数排序:的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
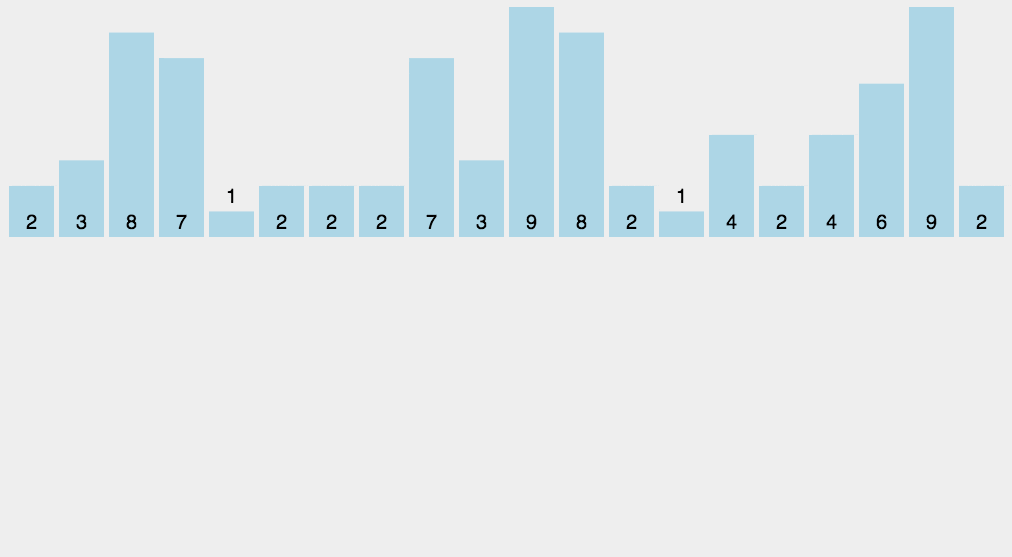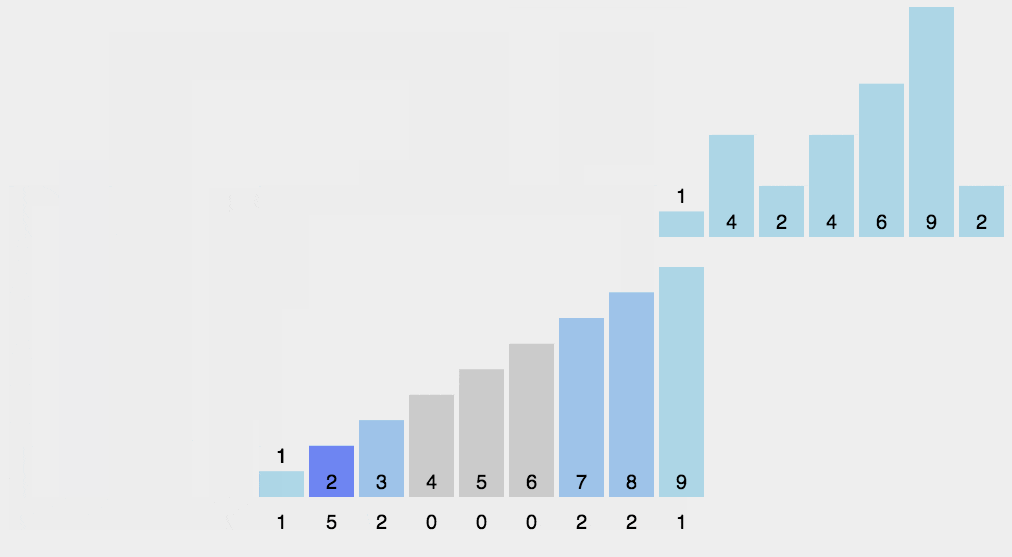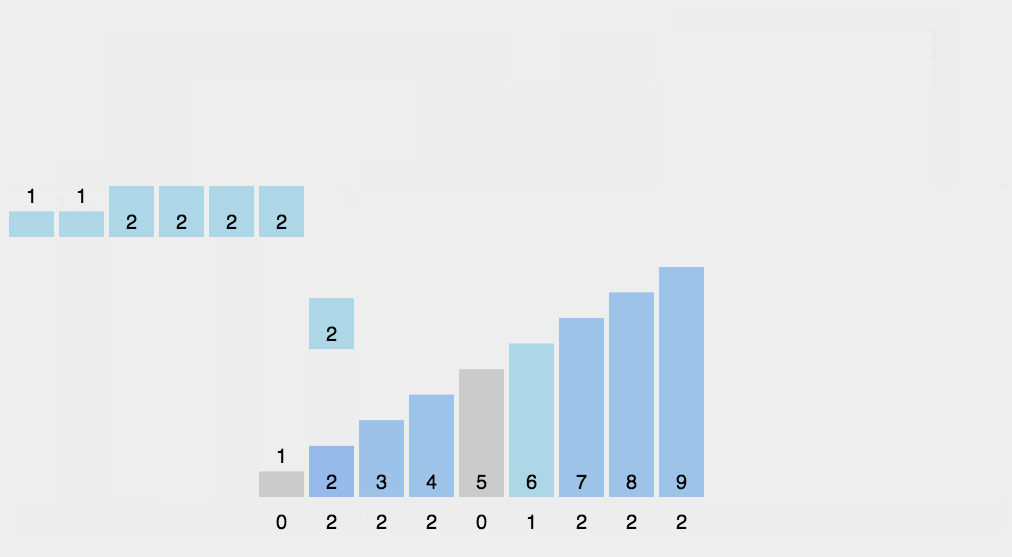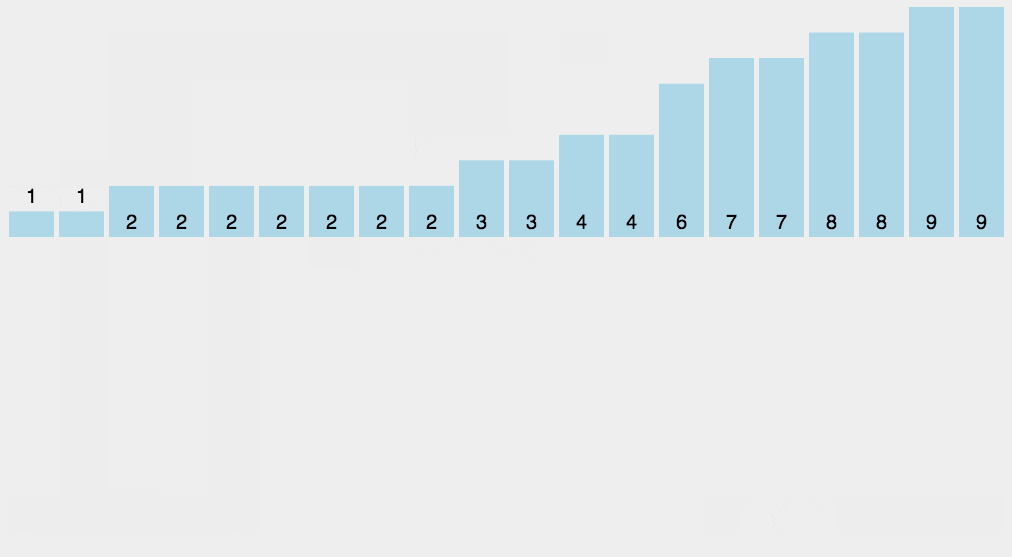
def countSort(arr):
output = [0 for i in range(256)]
count = [0 for i in range(256)]
ans = ["" for _ in arr]
for i in arr:
count[ord(i)] += 1
for i in range(256):
count[i] += count[i-1]
for i in range(len(arr)):
output[count[ord(arr[i])]-1] = arr[i]
count[ord(arr[i])] -= 1
for i in range(len(arr)):
ans[i] = output[i]
return ans
arr = "wwwnowcodercom"
ans = countSort(arr)
print("字符数组排序 %s" %("".join(ans)))运行结果:
字符数组排序 ccdemnooorwwww
希尔排序:也称递减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序。
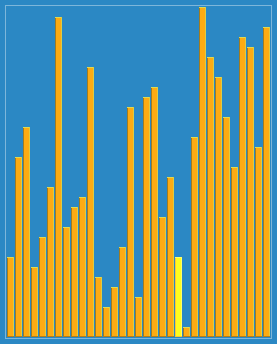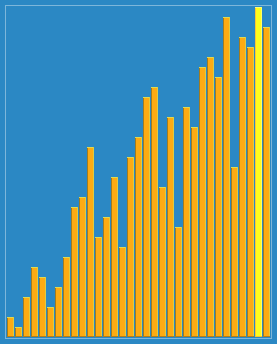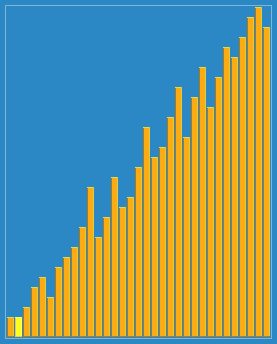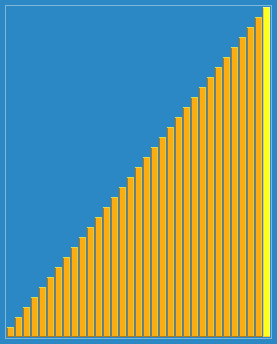
def shellSort(arr):
n = len(arr)
gap = int(n/2)
while gap > 0:
for i in range(gap, n):
temp = arr[i]
j = i
while j >= gap and arr[j-gap] > temp:
arr[j] = arr[j-gap]
j -= gap
arr[j] = temp
gap = int(gap/2)
return arr
arr = [12, 34, 54, 2, 3, 2, 5]
print("排序前:")
print(arr)
print("排序后:")
print(shellSort(arr))运行结果:
排序前:
[12, 34, 54, 2, 3, 2, 5]
排序后:
[2, 2, 3, 5, 12, 34, 54]
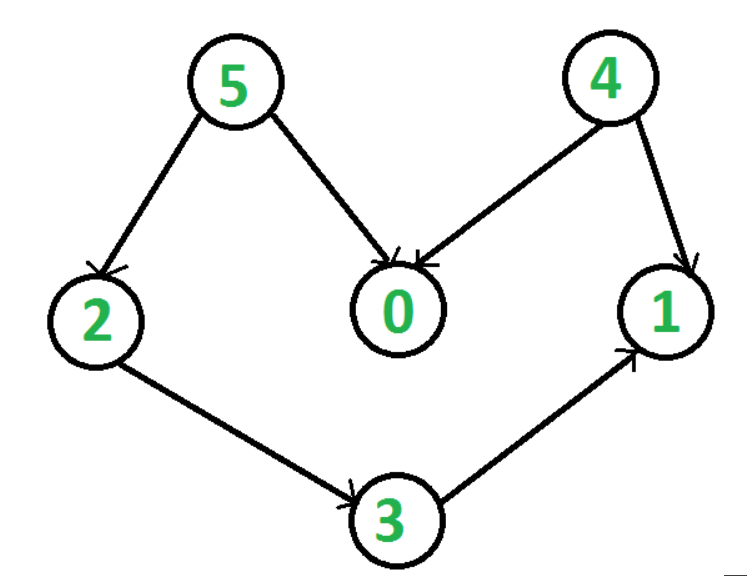
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。拓扑排序是一种将集合上的偏序转换为全序的操作。
在图论中,由一个有向无环图的顶点组成的序列,当且仅当满足下列条件时,称为该图的一个拓扑排序(英语:Topological sorting):
每个顶点出现且只出现一次;若A在序列中排在B的前面,则在图中不存在从B到A的路径。
from collections import defaultdict
class Graph:
def __init__(self, vertices):
self.graph = defaultdict(list)
self.V = vertices
def addEdge(self, u, v):
self.graph[u].append(v)
def topologicalSortUtil(self, v, visited, stack):
visited[v] = True
for i in self.graph[v]:
if visited[i] == False:
self.topologicalSortUtil(i, visited, stack)
stack.insert(0,v)
def topologicalSort(self):
visited = [False]*self.V
stack = []
for i in range(self.V):
if visited[i] == False:
self.topologicalSortUtil(i, visited, stack)
print(stack)
g= Graph(6)
g.addEdge(5, 2)
g.addEdge(5, 0)
g.addEdge(4, 0)
g.addEdge(4, 1)
g.addEdge(2, 3)
g.addEdge(3, 1)
print("拓扑排序结果:")
g.topologicalSort()运行结果:
拓扑排序结果:
[5, 4, 2, 3, 1, 0]
以上がPython の検索および並べ替えアルゴリズムのサンプル コード分析の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。