14 のアトリビューション アルゴリズムを理解して統合し、ニューラル ネットワークを解釈可能にする
DNN はさまざまな実用的なアプリケーションで広範な成功を収めてきましたが、DNN がどのように意思決定を行うかを説明するのが難しいため、そのプロセスはブラック ボックスとみなされることがよくあります。解釈可能性の欠如は DNN の信頼性を損なうため、自動運転や AI 医療などの一か八かのタスクへの DNN の広範な適用を妨げます。したがって、説明可能な DNN はますます注目を集めています。
DNN を説明するための典型的な観点として、アトリビューション手法は、ネットワーク出力に対する各入力変数の帰属/重要度/寄与スコアを計算することを目的としています。たとえば、画像分類用の事前トレーニング済み DNN と入力画像が与えられた場合、各入力変数の属性スコアは、分類信頼スコアに対する各ピクセルの数値的影響を指します。
研究者たちは近年、多くのアトリビューション手法を提案してきましたが、そのほとんどは異なるヒューリスティックに基づいています。現在、これらの帰属方法の正しさをテストするための、または少なくともそれらの中核的なメカニズムを数学的に解明するための統一された理論的観点が欠如しています。
研究者たちは、さまざまなアトリビューション方法を統一しようと試みてきましたが、これらの研究ではいくつかの方法しか取り上げられていません。
この記事では、「14 の入力単位重要度帰属アルゴリズムの固有メカニズムの統一的な説明」を提案します。

#論文アドレス: https://arxiv.org/pdf/2303.01506.pdf
#実際、「移行に対する耐性を向上させる 12 のアルゴリズム」であろうと、「14 の入力ユニット重要度属性アルゴリズム」であろうと、それらはすべてエンジニアリング アルゴリズムによって最も大きな打撃を受けます。これら 2 つの分野では、ほとんどのアルゴリズムが経験的なものであり、人々は実験的な経験や直観的な理解に基づいて、いくつかのもっともらしい工学アルゴリズムを設計します。ほとんどの研究では、「入力ユニットの重要性が正確に何であるか」について厳密な定義や理論的な実証が行われていません。いくつかの研究では、特定の実証が行われていますが、多くの場合、それらは非常に不完全です。もちろん、「厳密な定義と実証の欠如」という問題は人工知能の分野全体に浸透していますが、特にこれら 2 つの方向で顕著です。
- まず、解釈可能な機械学習の分野に多数の経験的アトリビューション アルゴリズムが氾濫している環境において、「14 個すべてのアトリビューション アルゴリズム (ニューラル ネットワーク入力の解釈)」を実証したいと考えています。ユニット重要度アルゴリズムのメカニズムは、ニューラル ネットワークによってモデル化されたインタラクション ユーティリティの分布として表現でき、異なる帰属アルゴリズムは異なるインタラクション ユーティリティの分布比率に対応します。このように、異なるアルゴリズムはまったく異なる設計の焦点を持っていますが (たとえば、一部のアルゴリズムは概要を示した目的関数を持ち、一部のアルゴリズムは純粋なパイプラインです)、数学的には、これらのアルゴリズムは「インタラクション ユーティリティ」「ディストリビューション」に含めることができることがわかりました。 」 物語論理の。
- 上記の対話型ユーティリティ割り当てフレームワークに基づいて、属性アルゴリズムによって予測される入力ユニットの重要性を測定するために、ニューラル ネットワークの入力ユニット重要度属性アルゴリズムの 3 つの評価基準をさらに提案できます。妥当な値ですか?
研究における本当の難しさは、さまざまな経験的帰属アルゴリズムが異なる直観に基づいて構築されていることが多く、それぞれの論文が独自の観点から「自分自身を正当化する」ことのみを目的としていることです。それぞれの設計帰属アルゴリズムさまざまな直観や視点に基づいていますが、さまざまなアルゴリズムの本質を統一的に記述するための標準化された数学言語がありません。
アルゴリズムのレビュー
数学について話す前に、この記事では以前のアルゴリズムを直感的なレベルから簡単にレビューします。1. 勾配ベースのアトリビューション アルゴリズム。 このタイプのアルゴリズムは一般に、各入力ユニットに対するニューラル ネットワークの出力の勾配が入力ユニットの重要性を反映できると考えられています。たとえば、Gradient*Input アルゴリズムは、入力単位の重要性を、勾配と入力単位値の要素ごとの積としてモデル化します。勾配は入力単位の局所的な重要度のみを反映できることを考慮して、スムーズ 勾配および統合勾配アルゴリズムは、平均勾配と入力単位値の要素ごとの積として重要度をモデル化します。ここで、これら 2 つの方法における平均勾配は、ドメイン内の勾配の平均値、または入力サンプルとベースライン点の間の線形補間点の平均勾配。同様に、Grad-CAM アルゴリズムは、各チャネルのすべての特徴勾配にわたるネットワーク出力の平均を取得して、重要度スコアを計算します。さらに、Expected Gradients アルゴリズムは、単一のベンチマーク ポイントを選択すると偏ったアトリビューション結果が得られることが多いと考えており、異なるベンチマーク ポイントの下での Integrated Gradients アトリビューション結果の期待値としてモデルの重要性を提案します。 #2. レイヤーごとのバックプロパゲーションに基づくアトリビューション アルゴリズム。 ディープ ニューラル ネットワークは非常に複雑なことが多く、ニューラル ネットワークの各層の構造は比較的単純です (たとえば、深いフィーチャは通常、浅いフィーチャの線形加算と非線形活性化関数です)。そのため、次の重要性の分析が容易になります。浅い特徴から深い特徴まで。したがって、このタイプのアルゴリズムは、中間レベルの特徴の重要度を推定し、これらの重要度を層ごとに入力層まで伝播することによって、入力ユニットの重要度を取得します。このカテゴリのアルゴリズムには、LRP-epsilon、LRP-alphabeta、Deep Taylor、DeepLIFT Rescale、DeepLIFT RevealCancel、DeepShap などが含まれます。異なるバックプロパゲーション アルゴリズム間の基本的な違いは、層ごとに異なる重要度伝播ルールが使用されることです。 #3. オクルージョンベースのアトリビューション アルゴリズム。 このタイプのアルゴリズムは、モデル出力に対する入力ユニットのオクルージョンの影響に基づいて、入力ユニットの重要性を推測します。たとえば、Occlusion-1 (オクルージョン パッチ) アルゴリズムは、i 番目のピクセル (ピクセル ブロック) の重要性を、ピクセル i がオクルージョンされていない場合と、他のピクセルがオクルージョンされていない場合にオクルージョンされる場合の出力の変化としてモデル化します。 Shapley 値アルゴリズムは、他のピクセルの考えられるすべてのオクルージョン状況を包括的に考慮し、異なるオクルージョン状況下でピクセル i に対応する出力の平均変化としての重要性をモデル化します。研究により、Shapley 値は線形性、ダミー、対称性、効率性の公理を満たす唯一の帰属アルゴリズムであることが証明されています。 さまざまな経験的アトリビューション アルゴリズムを徹底的に研究した後、次のような質問について考えずにはいられません。数学的レベル ニューラル ネットワークの属性によってどのような問題が解決されますか?多くの経験的帰属アルゴリズムの背後に、統一された数学的モデリングとパラダイムはあるのでしょうか?この目的を達成するために、帰属の定義から始めて上記の問題を検討してみます。アトリビューションとは、ニューラル ネットワーク出力に対する各入力ユニットの重要度スコア/寄与を指します。したがって、上記の問題を解決する鍵は、(1) 「ネットワーク出力に対する入力ユニットの影響メカニズム」を数学レベルでモデル化し、(2) 重要度の設計にこの影響メカニズムを使用する経験的帰属アルゴリズムがどれだけあるのかを説明することです。帰属式。 最初の重要なポイントに関して、私たちの研究では、各入力ユニットがニューラル ネットワークの出力に 2 つの方法で影響を与えることが多いことがわかりました。一方、ある入力装置が他の入力装置に依存することなく独立して動作し、ネットワークの出力に影響を与えることを「独立効果」といいます。一方、入力装置が他の入力装置と連携して一定のパターンを形成することにより、ネットワークの出力に影響を与えることを「相互作用効果」と呼びます。私たちの理論は、ニューラル ネットワークの出力を、異なる入力変数の独立した効果と、異なるセットの入力変数間の相互作用の効果に厳密に分解できることを証明しています。 このうち、14 の経験的アトリビューション アルゴリズムの内部メカニズムを統合する
 は i 番目の入力ユニットの独立した効果を表し、
は i 番目の入力ユニットの独立した効果を表し、 は、セット内の複数の効果 S 入力ユニット間の相互作用効果。 2 番目の重要な点に関して、既存の 14 個すべての経験的帰属アルゴリズムの内部メカニズムが、上記の独立ユーティリティと対話ユーティリティの割り当てと、異なる属性を表現できることを発見しました。アルゴリズムは、独立ユーティリティと対話ユーティリティを分散します。ニューラル ネットワーク入力ユニットを異なる割合で使用します。具体的には、
は、セット内の複数の効果 S 入力ユニット間の相互作用効果。 2 番目の重要な点に関して、既存の 14 個すべての経験的帰属アルゴリズムの内部メカニズムが、上記の独立ユーティリティと対話ユーティリティの割り当てと、異なる属性を表現できることを発見しました。アルゴリズムは、独立ユーティリティと対話ユーティリティを分散します。ニューラル ネットワーク入力ユニットを異なる割合で使用します。具体的には、  # とします。 は、i 番目の入力単位の帰属スコアを表します。我々は、14 個すべての経験的帰属アルゴリズムによって得られた
# とします。 は、i 番目の入力単位の帰属スコアを表します。我々は、14 個すべての経験的帰属アルゴリズムによって得られた  が次の数学的パラダイム (つまり、独立効用と対話効用の加重和) として一様に表現できることを厳密に証明します。
が次の数学的パラダイム (つまり、独立効用と対話効用の加重和) として一様に表現できることを厳密に証明します。 
は、i 番目の入力ユニット  ## に割り当てられた j 番目の入力ユニットの独立した効果の割合を反映します。 # は、集合 S 内の複数の入力ユニット間の相互作用効果のうち、i 番目の入力ユニットに割り当てられる割合を表します。多くのアトリビューション アルゴリズムの「根本的な違い」は、異なるアトリビューション アルゴリズムが異なる割り当て比率
## に割り当てられた j 番目の入力ユニットの独立した効果の割合を反映します。 # は、集合 S 内の複数の入力ユニット間の相互作用効果のうち、i 番目の入力ユニットに割り当てられる割合を表します。多くのアトリビューション アルゴリズムの「根本的な違い」は、異なるアトリビューション アルゴリズムが異なる割り当て比率  に対応することです。
に対応することです。  #表 1 は、14 の異なるアトリビューション アルゴリズムが独立した効果とインタラクティブな効果をどのように割り当てるかを示しています。
#表 1 は、14 の異なるアトリビューション アルゴリズムが独立した効果とインタラクティブな効果をどのように割り当てるかを示しています。

はそれぞれテイラー独立効果とテイラー相互作用効果を表し、 を満たします。 は、独立したエフェクト
は、独立したエフェクト 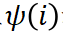 とインタラクティブなエフェクト
とインタラクティブなエフェクト  を改良したものです。
を改良したものです。














##アトリビューション アルゴリズムの信頼性を評価するための 3 つの主要な基準

この研究でアトリビューション アルゴリズムの公開メカニズムが明らかになったことで、同じ理論的枠組みの下で、さまざまなアトリビューション アルゴリズムの信頼性を公平に評価し、比較できるようになります。具体的には、あるアトリビューションアルゴリズムが独立効果と相互作用効果を公平かつ合理的に配分しているかどうかを評価するために、以下の3つの評価基準を提案します。
(1)ガイドライン 1: 割り当てプロセスですべての独立した効果と対話型効果をカバーします。ニューラル ネットワークの出力を独立した効果とインタラクティブな効果に分解した後、信頼できるアトリビューション アルゴリズムは、割り当てプロセスですべての独立した効果とインタラクティブな効果を可能な限りカバーする必要があります。たとえば、「I'm not happy」という文への帰属は、「I'm」、「not」、「happy」という 3 つの単語の独立した効果をすべてカバーする必要があり、また、J (私は、そうではない)、J (私は、幸せです) もカバーする必要があります。 ) 、J (そうではない、幸せではない)、J (私は、そうではない、幸せではない) など、考えられるすべての相互作用効果。
(2)ガイドライン 2: 独立したエフェクトやインタラクションを無関係な入力ユニットに割り当てないでください。 i 番目の入力ユニットの独立したエフェクトは、i 番目の入力ユニットにのみ割り当てられ、他の入力ユニットには割り当てられません。同様に、集合 S 内の入力ユニット間の相互作用効果は、集合 S 内の入力ユニットにのみ割り当てられるべきであり、集合 S の外の入力ユニット(相互作用に参加していない)には割り当てられるべきではありません。たとえば、「not」と「happy」の間の相互作用効果を「I'm」という単語に割り当てるべきではありません。
(3) ガイドライン 3: 割り当てを完了する 。それぞれの独立したエフェクト (インタラクション エフェクト) は、対応する入力ユニットに完全に割り当てられる必要があります。言い換えれば、ある独立した効果(相互作用効果)によって対応するすべての入力ユニットに割り当てられた属性値は、完全に独立した効果(相互作用効果)の値に合計される必要があります。たとえば、交互作用効果 J (not、happy) は、効果  (not、happy) の一部を単語 not に割り当て、効果の一部
(not、happy) の一部を単語 not に割り当て、効果の一部  を割り当てます。 (違う、幸せ) 幸せという言葉を贈ってください。したがって、分配率は
を割り当てます。 (違う、幸せ) 幸せという言葉を贈ってください。したがって、分配率は 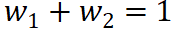 を満たす必要があります。
を満たす必要があります。
次に、これら 3 つの評価基準を使用して、上記の 14 の異なるアトリビューション アルゴリズムを評価しました (表 2 を参照)。アルゴリズムの Integrated Gradients、Expected Gradients、Shapley value、Deep Shap、DeepLIFT Rescale、DeepLIFT RevealCancel がすべての信頼性基準を満たしていることがわかりました。

表 2. 14 の異なるアトリビューション アルゴリズムが 3 つの信頼性を満たすかどうかのまとめ基準 評価基準。
著者の紹介この記事の著者であるDeng Huiqiは、中山大学の応用数学の博士号を取得しています。博士課程の在学中に、香港バプティスト大学のコンピュータ サイエンス学部とテキサス A&M 大学の客員学生として勤務し、現在は Zhang Quanshi のチームで博士研究員として研究を行っています。研究の方向性は主に信頼性・解釈可能な機械学習であり、ディープニューラルネットワークの帰属の重要性の説明、ニューラルネットワークの表現能力の説明などが含まれます。
Deng Huiqi は初期段階で多くの仕事をしました。張先生は、証明方法とシステムをよりスムーズにするために、最初の作業が完了した後、理論を再構成するのを手伝っただけです。鄧慧奇さんは卒業まであまり論文を書かなかったが、2021年末に張先生のもとに来てからは、ゲームインタラクションシステムの下で1年以上の間に、(1)ニューラルの共通表現ボトルネックの発見と理論的説明を含む3つの課題を遂行した。ネットワーク、つまりニューラル ネットワークは、中程度の複雑さのインタラクティブな表現をモデル化するのにさらに熟練していないことが示されています。この研究は幸運にも ICLR 2022 の口頭論文に選ばれ、レビュースコアはトップ 5 にランクされました (スコア 8 8 8 10)。 (2) この理論は、ベイジアン ネットワークの概念的表現傾向を証明し、ベイジアン ネットワークの分類性能、汎化能力、敵対的堅牢性を説明するための新しい視点を提供します。 (3) トレーニング プロセス中にさまざまな複雑さのインタラクティブな概念を学習するニューラル ネットワークの能力を理論的に説明します。
以上が14 のアトリビューション アルゴリズムを理解して統合し、ニューラル ネットワークを解釈可能にするの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7560
7560
 15
15
 1384
1384
 52
52
 84
84
 11
11
 28
28
 98
98
 CLIP-BEVFormer: BEVFormer 構造を明示的に監視して、ロングテール検出パフォーマンスを向上させます。
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: BEVFormer 構造を明示的に監視して、ロングテール検出パフォーマンスを向上させます。
Mar 26, 2024 pm 12:41 PM
上記および筆者の個人的な理解: 現在、自動運転システム全体において、認識モジュールが重要な役割を果たしている。道路を走行する自動運転車は、認識モジュールを通じてのみ正確な認識結果を得ることができる。下流の規制および制御モジュール自動運転システムでは、タイムリーかつ正確な判断と行動決定が行われます。現在、自動運転機能を備えた自動車には通常、サラウンドビューカメラセンサー、ライダーセンサー、ミリ波レーダーセンサーなどのさまざまなデータ情報センサーが搭載されており、さまざまなモダリティで情報を収集して正確な認識タスクを実現しています。純粋な視覚に基づく BEV 認識アルゴリズムは、ハードウェア コストが低く導入が容易であるため、業界で好まれており、その出力結果はさまざまな下流タスクに簡単に適用できます。
 C++ での機械学習アルゴリズムの実装: 一般的な課題と解決策
Jun 03, 2024 pm 01:25 PM
C++ での機械学習アルゴリズムの実装: 一般的な課題と解決策
Jun 03, 2024 pm 01:25 PM
C++ の機械学習アルゴリズムが直面する一般的な課題には、メモリ管理、マルチスレッド、パフォーマンスの最適化、保守性などがあります。解決策には、スマート ポインター、最新のスレッド ライブラリ、SIMD 命令、サードパーティ ライブラリの使用、コーディング スタイル ガイドラインの遵守、自動化ツールの使用が含まれます。実践的な事例では、Eigen ライブラリを使用して線形回帰アルゴリズムを実装し、メモリを効果的に管理し、高性能の行列演算を使用する方法を示します。
 C++sort 関数の基礎となる原則とアルゴリズムの選択を調べる
Apr 02, 2024 pm 05:36 PM
C++sort 関数の基礎となる原則とアルゴリズムの選択を調べる
Apr 02, 2024 pm 05:36 PM
C++sort 関数の最下層はマージ ソートを使用し、その複雑さは O(nlogn) で、クイック ソート、ヒープ ソート、安定したソートなど、さまざまなソート アルゴリズムの選択肢を提供します。
 人工知能は犯罪を予測できるのか? CrimeGPT の機能を調べる
Mar 22, 2024 pm 10:10 PM
人工知能は犯罪を予測できるのか? CrimeGPT の機能を調べる
Mar 22, 2024 pm 10:10 PM
人工知能 (AI) と法執行機関の融合により、犯罪の予防と検出の新たな可能性が開かれます。人工知能の予測機能は、犯罪行為を予測するためにCrimeGPT (犯罪予測技術) などのシステムで広く使用されています。この記事では、犯罪予測における人工知能の可能性、その現在の応用、人工知能が直面する課題、およびこの技術の倫理的影響について考察します。人工知能と犯罪予測: 基本 CrimeGPT は、機械学習アルゴリズムを使用して大規模なデータセットを分析し、犯罪がいつどこで発生する可能性があるかを予測できるパターンを特定します。これらのデータセットには、過去の犯罪統計、人口統計情報、経済指標、気象パターンなどが含まれます。人間のアナリストが見逃す可能性のある傾向を特定することで、人工知能は法執行機関に力を与えることができます
 改良された検出アルゴリズム: 高解像度の光学式リモートセンシング画像でのターゲット検出用
Jun 06, 2024 pm 12:33 PM
改良された検出アルゴリズム: 高解像度の光学式リモートセンシング画像でのターゲット検出用
Jun 06, 2024 pm 12:33 PM
01 今後の概要 現時点では、検出効率と検出結果の適切なバランスを実現することが困難です。我々は、光学リモートセンシング画像におけるターゲット検出ネットワークの効果を向上させるために、多層特徴ピラミッド、マルチ検出ヘッド戦略、およびハイブリッドアテンションモジュールを使用して、高解像度光学リモートセンシング画像におけるターゲット検出のための強化されたYOLOv5アルゴリズムを開発しました。 SIMD データセットによると、新しいアルゴリズムの mAP は YOLOv5 より 2.2%、YOLOX より 8.48% 優れており、検出結果と速度のバランスがより優れています。 02 背景と動機 リモート センシング技術の急速な発展に伴い、航空機、自動車、建物など、地表上の多くの物体を記述するために高解像度の光学式リモート センシング画像が使用されています。リモートセンシング画像の判読における物体検出
 Jiuzhang Yunji DataCanvas マルチモーダル大規模モデル プラットフォームの実践と考察
Oct 20, 2023 am 08:45 AM
Jiuzhang Yunji DataCanvas マルチモーダル大規模モデル プラットフォームの実践と考察
Oct 20, 2023 am 08:45 AM
1. マルチモーダル大型モデルの発展の歴史 上の写真は、1956 年に米国のダートマス大学で開催された最初の人工知能ワークショップです。このカンファレンスが人工知能開発の始まりとも考えられています。記号論理学の先駆者たち(前列中央の神経生物学者ピーター・ミルナーを除く)。しかし、この記号論理理論は長い間実現できず、1980 年代と 1990 年代に最初の AI の冬の到来さえもたらしました。最近の大規模な言語モデルが実装されて初めて、ニューラル ネットワークが実際にこの論理的思考を担っていることがわかりました。神経生物学者ピーター ミルナーの研究は、その後の人工ニューラル ネットワークの開発に影響を与えました。彼が参加に招待されたのはこのためです。このプロジェクトでは。
 58 ポートレート プラットフォームの構築におけるアルゴリズムの適用
May 09, 2024 am 09:01 AM
58 ポートレート プラットフォームの構築におけるアルゴリズムの適用
May 09, 2024 am 09:01 AM
1. 58 Portraits プラットフォーム構築の背景 まず、58 Portraits プラットフォーム構築の背景についてお話ししたいと思います。 1. 従来のプロファイリング プラットフォームの従来の考え方ではもはや十分ではありません。ユーザー プロファイリング プラットフォームを構築するには、複数のビジネス分野からのデータを統合して、ユーザーの行動や関心を理解するためのデータ マイニングも必要です。最後に、ユーザー プロファイル データを効率的に保存、クエリ、共有し、プロファイル サービスを提供するためのデータ プラットフォーム機能も必要です。自社構築のビジネス プロファイリング プラットフォームとミドルオフィス プロファイリング プラットフォームの主な違いは、自社構築のプロファイリング プラットフォームは単一のビジネス ラインにサービスを提供し、オンデマンドでカスタマイズできることです。ミッドオフィス プラットフォームは複数のビジネス ラインにサービスを提供し、複雑な機能を備えていることです。モデリングを提供し、より一般的な機能を提供します。 2.58 中間プラットフォームのポートレート構築の背景のユーザーのポートレート 58
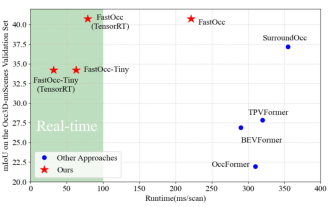 SOTA をリアルタイムで追加すると、大幅に増加します。 FastOcc: より高速な推論と展開に適した Occ アルゴリズムが登場しました。
Mar 14, 2024 pm 11:50 PM
SOTA をリアルタイムで追加すると、大幅に増加します。 FastOcc: より高速な推論と展開に適した Occ アルゴリズムが登場しました。
Mar 14, 2024 pm 11:50 PM
上記と著者の個人的な理解は、自動運転システムにおいて、認識タスクは自動運転システム全体の重要な要素であるということです。認識タスクの主な目的は、自動運転車が道路を走行する車両、路側の歩行者、運転中に遭遇する障害物、道路上の交通標識などの周囲の環境要素を理解して認識できるようにすることで、それによって下流のシステムを支援できるようにすることです。モジュール 正しく合理的な決定と行動を行います。自動運転機能を備えた車両には、通常、サラウンドビューカメラセンサー、ライダーセンサー、ミリ波レーダーセンサーなど、さまざまな種類の情報収集センサーが装備されており、自動運転車が正確に認識し、認識できるようにします。周囲の環境要素を理解することで、自動運転車が自動運転中に正しい判断を下せるようになります。頭




