
負のループがない(ループの重みの合計が負である)ときに負の重みエッジに遭遇した場合、ベルマン・フォードアルゴリズムを使用して最短距離を解くことができます。パス。このアルゴリズムの利点は、負の変数重みの場合を処理でき、実装が簡単であることですが、欠点は、時間が複雑すぎることです。ただし、効率を高めるためにアルゴリズムをいくつかの方法で最適化できます。
Bellman-Ford アルゴリズムはダイクストラ アルゴリズムに似ており、どちらも緩和操作に基づいています。ダイクストラ アルゴリズムは貪欲な方法を使用して、最小の重みを持つ未処理のノードを選択し、それを緩和しますが、ベルマン フォード アルゴリズムはすべてのエッジを合計 n-1 回緩和します。 n 番目の操作がまだ緩和できる場合は、負のループが存在する必要があります。負のループは最短パスの長さを継続的に短縮できるためです。ノードの数が n、エッジの数が m である場合、ベルマン フォード アルゴリズムの最大実行時間は O(nm) です。
1 データ構造
エッジは緩和に使用する必要があるため、エッジ セット配列ストレージが使用されます。各エッジには 3 つのドメインがあります: 2 つの端点 a と b、およびエッジの重み w
2 緩和操作
すべてのエッジ j(a,b,w) について、dis[ e[j] b]>dis[e[j].a] e[j].w の場合は緩和され、dis[e[j]b]=dis[e[j].a] e[j] .w 。このうち、dis[v]は始点からノードvまでの最短経路長を表します。
3 緩和操作をn-1回繰り返します
4 ネガティブループ判定
もう一度緩和操作を行い、それでも緩和できれば権利ありです負のループ。
package graph.bellmanford;
import java.util.Scanner;
public class BellmanFord {
static node e[] = new node[210];
static int dis[] = new int[110];
static int n;
static int m;
static int cnt = 0;
static {
for (int i = 0; i < e.length; i++) {
e[i] = new node();
}
}
static void add(int a, int b, int w) {
e[cnt].a = a;
e[cnt].b = b;
e[cnt++].w = w;
}
static boolean bellman_ford(int u) { // 求源点 u 到其它顶点的最短路径长度,判负环
for (int i = 0; i < dis.length; i++) {
dis[i] = 0x3f;
}
dis[u] = 0;
for (int i = 1; i < n; i++) { // 执行 n-1 次
boolean flag = false;
for (int j = 0; j < m; j++) // 边数 m 或 cnt
if (dis[e[j].b] > dis[e[j].a] + e[j].w) {
dis[e[j].b] = dis[e[j].a] + e[j].w;
flag = true;
}
if (!flag)
return false;
}
for (int j = 0; j < m; j++) // 再执行 1 次,还能松弛说明有环
if (dis[e[j].b] > dis[e[j].a] + e[j].w)
return true;
return false;
}
static void print() { // 输出源点到其它节点的最短距离
System.out.println("最短距离:");
for (int i = 1; i <= n; i++)
System.out.print(dis[i] + " ");
System.out.println();
}
public static void main(String[] args) {
int a, b, w;
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
for (int i = 0; i < m; i++) {
a = scanner.nextInt();
b = scanner.nextInt();
w = scanner.nextInt();
add(a, b, w);
}
if (bellman_ford(1)) // 判断负环
System.out.println("有负环!");
else
print();
}
}
class node {
int a;
int b;
int w;
}1 ネガティブ ループなしのテスト
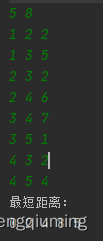
2 ネガティブ ループ テストを使用したテスト
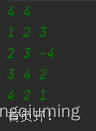
以上がJava Bellman-Ford アルゴリズムの原理と実装方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。