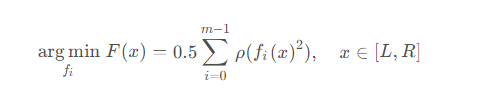いわゆる線形最小二乗法は、方程式を解くことの連続であると理解できますが、異なるのは、未知の量が方程式の数よりはるかに小さい場合、解けない問題が得られることです。最小二乗法の本質は、誤差を最小限に抑えながら未知の数値に値を割り当てることです。
最小二乗法は非常に古典的なアルゴリズムであり、私たちは高校でこの名前に触れたことがある、非常に一般的に使用されるアルゴリズムです。私は以前、線形最小二乗の原理と Python での実装について書きました: 最小二乗とその Python 実装; および scipy で非線形最小二乗を呼び出す方法: 非線形最小二乗(記事の最後にある補足コンテンツ) ;疎行列の最小二乗法である疎行列最小二乗法もあります。
以下では、numpy と scipy で実装された線形最小二乗法について説明し、2 つの速度を比較します。
numpy の実装
最小二乗法は numpy に実装されています。つまり、lstsq(a,b) は、a@x=b と同様に x を解くために使用されます。ここで、a は M× です。 N 行列; b が M 行のベクトルのとき、それは連立一次方程式を解くのとまったく同じです。 Ax=b のような連立方程式の場合、A がフルランク シミュレーションの場合は x=A−1 b と表現でき、それ以外の場合は x=(AT と表現できます) A)−1 AT b.
b が M×K の行列の場合、列ごとに x のセットが計算されます。
戻り値は 4 つあり、フィッティングによって得られた x、フィッティング誤差、行列 a のランク、行列 a の単一値形式です。
import numpy as np
np.random.seed(42)
M = np.random.rand(4,4)
x = np.arange(4)
y = M@x
xhat = np.linalg.lstsq(M,y)
print(xhat[0])
#[0. 1. 2. 3.] ログイン後にコピー
scipy パッケージ scipy.linalg は最小二乗関数も提供します。関数名も lstsq で、そのパラメーター リストは
lstsq(a, b, cond=None, overwrite_a=False, overwrite_b=False, check_finite=True, lapack_driver=None) ログイン後にコピー
です。ここで、a、b は Ax です= b. どちらもオーバーライド可能なスイッチを提供します。これらを True に設定すると、実行時間を節約できます。さらに、この関数は、linalg の多くの関数が持つオプションである有限性チェックもサポートしています。戻り値は numpy の最小二乗関数と同じです。
cond は、特異値のしきい値を示す浮動小数点パラメータです。特異値が cond 未満の場合、特異値は破棄されます。
lapack_driver は文字列オプションで、LAPACK のどのアルゴリズム エンジンが選択されているかを示します。オプションで「gelsd」、「gelsy」、「gelss」です。
import scipy.linalg as sl
xhat1 = sl.lstsq(M, y)
print(xhat1[0])
# [0. 1. 2. 3.] ログイン後にコピー
速度比較 最後に、2 つの最小二乗関数セットの速度比較を行います
from timeit import timeit
N = 100
A = np.random.rand(N,N)
b = np.arange(N)
timeit(lambda:np.linalg.lstsq(A, b), number=10)
# 0.015487500000745058
timeit(lambda:sl.lstsq(A, b), number=10)
# 0.011151800004881807 ログイン後にコピー
今回は、2 つの関数はそれほど離れていません。つまり、行列の次元が 500 に拡大されても、この 2 つはほぼ同じになります。
N = 500
A = np.random.rand(N,N)
b = np.arange(N)
timeit(lambda:np.linalg.lstsq(A, b), number=10)
0.389679799991427
timeit(lambda:sl.lstsq(A, b), number=10)
0.35642060000100173 ログイン後にコピー
補足 Python は非線形最小二乗法を呼び出します
導入とコンストラクター
In In scipy さん、非線形最小二乗法の目的は、誤差関数の二乗和を最小化する一連の関数を見つけることです。これは次の式で表されます
ここで、ρ は損失関数を表し、f
i(x) の前処理として理解できます。
scipy.optimize は、
least_squares(fun, x0, jac, bounds, method, ftol, xtol, gtol, x_scale, f_scale, loss, jac_sparsity, max_nfev, verbose, args, kwargs) ログイン後にコピー
として定義される非線形最小二乗関数 minimum_squares をカプセル化します。このうち、func と x0 は必須パラメータであり、func は解く関数、x0 はfunction input の初期値。これら 2 つのパラメータにはデフォルト値はありません。これらは入力する必要があるパラメータです。
bound は解決間隔です。デフォルトは (−∞,∞) です。verbose が 1 の場合、終了出力が表示されます。verbose が 2 の場合、操作中の詳細情報が出力されます。 。さらに、次のパラメータを使用してエラーを制御しますが、これは比較的簡単です。
備考 10 -8#機能許容範囲 #xtol #10-8 1.0 f_scaleloss为损失函数,就是上面公式中的ρ \rhoρ,默认为linear,可选值包括
迭代策略
上面的公式仅给出了算法的目的,但并未暴露其细节。关于如何找到最小值,则需要确定搜索最小值的方法,method为最小值搜索的方案,共有三种选项,默认为trf
这三种方法都是信赖域方法的延申,信赖域的优化思想其实就是从单点的迭代变成了区间的迭代,由于本文的目的是介绍scipy中所封装好的非线性最小二乘函数,故而仅对其原理做简略的介绍。
其中r为置信半径,假设在这个邻域内,目标函数可以近似为线性或二次函数,则可通过二次模型得到区间中的极小值点sk 。然后以这个极小值点为中心,继续优化信赖域所对应的区间。
雅可比矩阵
在了解了信赖域方法之后,就会明白雅可比矩阵在数值求解时的重要作用,而如何计算雅可比矩阵,则是接下来需要考虑的问题。jac参数为计算雅可比矩阵的方法,主要提供了三种方案,分别是基于两点的2-point;基于三点的3-point;以及基于复数步长的cs。一般来说,三点的精度高于两点,但速度也慢一倍。
此外,可以输入自定义函数来计算雅可比矩阵。
测试
最后,测试一下非线性最小二乘法
import numpy as np
from scipy.optimize import least_squares
def test(xs):
_sum = 0.0
for i in range(len(xs)):
_sum = _sum + (1-np.cos((xs[i]*i)/5)*(i+1))
return _sum
x0 = np.random.rand(5)
ret = least_squares(test, x0)
msg = f"最小值" + ", ".join([f"{x:.4f}" for x in ret.x])
msg += f"\nf(x)={ret.fun[0]:.4f}"
print(msg)
'''
最小值0.9557, 0.5371, 1.5714, 1.6931, 5.2294
f(x)=0.0000
''' ログイン後にコピー
以上がPython で最小二乗法を呼び出して実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
このウェブサイトの声明
この記事の内容はネチズンが自主的に寄稿したものであり、著作権は原著者に帰属します。このサイトは、それに相当する法的責任を負いません。盗作または侵害の疑いのあるコンテンツを見つけた場合は、admin@php.cn までご連絡ください。
PHPおよびPython:さまざまなパラダイムが説明されています
Apr 18, 2025 am 12:26 AM
PHPは主に手順プログラミングですが、オブジェクト指向プログラミング(OOP)もサポートしています。 Pythonは、OOP、機能、手続き上のプログラミングなど、さまざまなパラダイムをサポートしています。 PHPはWeb開発に適しており、Pythonはデータ分析や機械学習などのさまざまなアプリケーションに適しています。
PHPとPythonの選択:ガイド
Apr 18, 2025 am 12:24 AM
PHPはWeb開発と迅速なプロトタイピングに適しており、Pythonはデータサイエンスと機械学習に適しています。 1.PHPは、単純な構文と迅速な開発に適した動的なWeb開発に使用されます。 2。Pythonには簡潔な構文があり、複数のフィールドに適しており、強力なライブラリエコシステムがあります。
PHPとPython:彼らの歴史を深く掘り下げます
Apr 18, 2025 am 12:25 AM
PHPは1994年に発信され、Rasmuslerdorfによって開発されました。もともとはウェブサイトの訪問者を追跡するために使用され、サーバー側のスクリプト言語に徐々に進化し、Web開発で広く使用されていました。 Pythonは、1980年代後半にGuidovan Rossumによって開発され、1991年に最初にリリースされました。コードの読みやすさとシンプルさを強調し、科学的コンピューティング、データ分析、その他の分野に適しています。
Python vs. JavaScript:学習曲線と使いやすさ
Apr 16, 2025 am 12:12 AM
Pythonは、スムーズな学習曲線と簡潔な構文を備えた初心者により適しています。 JavaScriptは、急な学習曲線と柔軟な構文を備えたフロントエンド開発に適しています。 1。Python構文は直感的で、データサイエンスやバックエンド開発に適しています。 2。JavaScriptは柔軟で、フロントエンドおよびサーバー側のプログラミングで広く使用されています。
Sublime Code Pythonを実行する方法
Apr 16, 2025 am 08:48 AM
PythonコードをSublimeテキストで実行するには、最初にPythonプラグインをインストールし、次に.pyファイルを作成してコードを書き込み、Ctrl Bを押してコードを実行する必要があります。コードを実行すると、出力がコンソールに表示されます。
Windows 8でコードを実行できます
Apr 15, 2025 pm 07:24 PM
VSコードはWindows 8で実行できますが、エクスペリエンスは大きくない場合があります。まず、システムが最新のパッチに更新されていることを確認してから、システムアーキテクチャに一致するVSコードインストールパッケージをダウンロードして、プロンプトとしてインストールします。インストール後、一部の拡張機能はWindows 8と互換性があり、代替拡張機能を探すか、仮想マシンで新しいWindowsシステムを使用する必要があることに注意してください。必要な拡張機能をインストールして、適切に動作するかどうかを確認します。 Windows 8ではVSコードは実行可能ですが、開発エクスペリエンスとセキュリティを向上させるために、新しいWindowsシステムにアップグレードすることをお勧めします。
vscodeでコードを書く場所
Apr 15, 2025 pm 09:54 PM
Visual Studioコード(VSCODE)でコードを作成するのはシンプルで使いやすいです。 VSCODEをインストールし、プロジェクトの作成、言語の選択、ファイルの作成、コードの書き込み、保存して実行します。 VSCODEの利点には、クロスプラットフォーム、フリーおよびオープンソース、強力な機能、リッチエクステンション、軽量で高速が含まれます。
Visual StudioコードはPythonで使用できますか
Apr 15, 2025 pm 08:18 PM
VSコードはPythonの書き込みに使用でき、Pythonアプリケーションを開発するための理想的なツールになる多くの機能を提供できます。ユーザーは以下を可能にします。Python拡張機能をインストールして、コードの完了、構文の強調表示、デバッグなどの関数を取得できます。デバッガーを使用して、コードを段階的に追跡し、エラーを見つけて修正します。バージョンコントロールのためにGitを統合します。コードフォーマットツールを使用して、コードの一貫性を維持します。糸くずツールを使用して、事前に潜在的な問題を発見します。
See all articles