グラフは抽象的なデータ構造であり、その本質はツリー構造と同じです。
ツリーと比較すると、グラフは閉じており、ツリー構造はグラフ構造の前身とみなすことができます。ツリー構造に兄弟ノードや子ノード間の横のつながりを適用すると、グラフ構造を作成できます。
ツリーは、企業の組織構造など、1 対多のデータ構造を上から下に記述するのに適しています。
グラフは、複雑なグループの社会的関係など、より複雑な多対多のデータ構造を記述するのに適しています。
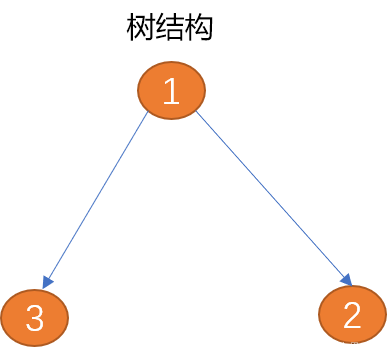
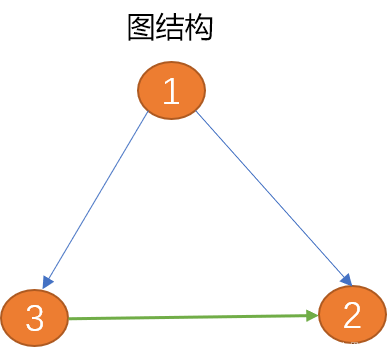
頂点:頂点はノードとも呼ばれ、グラフは頂点の集合と考えることができます。頂点自体にデータの意味があるため、頂点には「ペイロード」と呼ばれる追加情報が含まれます。
頂点には、現実世界の都市、地名、駅名、人物を指定できます...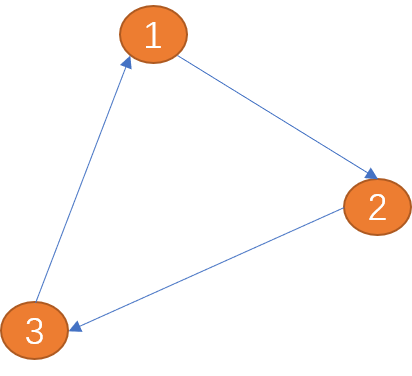
#エッジ: 画像の エッジは頂点間の関係を記述するために使用されます。エッジには方向がある場合と方向がない場合があり、方向のあるエッジは単方向エッジと双方向エッジに分類できます。
下図に示すように、(項目1)と(頂点2)の間のエッジは一方向のみ(矢印は方向を示します)を持ち、を一方向エッジと呼びます 。現実世界の一方通行に似ています。
(頂点 1) と (頂点 2) の間のエッジは 2 つの方向 (双方向矢印) を持ち、を双方向エッジと呼びます。 都市間の関係は双方向のエッジです。
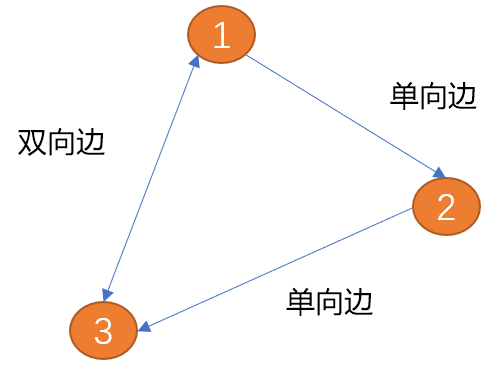
重み: エッジに値情報を追加でき、追加された値は weight と呼ばれます。重み付けされたエッジは、ある頂点から別の頂点への接続の強さを表します。
たとえば、実際の地下鉄路線では、重みは 2 つの駅間の時間の長さ、キロメートル、運賃を表すことができます...エッジは頂点間の関係を表し、重みは違いを表します。接続。#パス: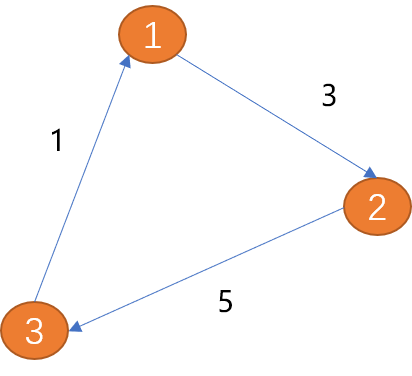 
まず、現実世界におけるパスの概念を理解します
例: ある都市から別の都市へ車で移動するには、まずルートを決定する必要があります。それは、 出発地から目的地までにどの都市を経由しなければならないかということです。何マイルかかりますか?
パスは、エッジで接続された一連の頂点であると言えます。複数のパスがあるため、ある項目ポイントから別の項目ポイントへのパスの説明は 1 つのタイプを参照しません。
グラフ構造内のパスを計算するにはどうすればよいですか?重み付けされていないパスの長さは、パス上のエッジの数です。
重み付きパスの長さは、パス上のエッジの重みの合計です。
上図に示すように、(頂点 1) から (頂点 3) までのパスの長さは 8 です。
開始点から開始し、最終的に開始点に戻る (終了点は開始点でもあります) ループを形成します。ループは特別なパスです。上記のように、
(V1, V2, V3, V1) はリングです。 グラフの種類:
要約すると、グラフは次のカテゴリに分類できます:
有向グラフ:無向グラフ:
重み付きグラフ:
非循環グラフ:
有向非循環グラフ:
1.2 グラフの定義
すべての頂点は、情報のセットを形成します。これは、ここでは V で表されます (たとえば、マップ プログラムでは、すべての都市が 1 つの頂点セットで形成されます)。
すべてのエッジは集合情報を構成し、ここでは E (都市間の関係の記述) で表されます。
エッジをどのように記述するか?
エッジは、アイテム ポイント間の関係を表すために使用されます。したがって、エッジには 3 つのメタデータ (開始点、終了点、重み) を含めることができます。もちろん重みを省略することもできますが、一般にグラフを学習する場合は重み付きグラフを指します。
G を使用してグラフを表す場合、G = (V, E) となります。各エッジは、タプル (fv, ev) またはトリプレット (fv,ev,w) で記述できます。
fv は開始点を表し、ev は終了点を表します。また、fv、ev データは V コレクションで参照される必要があります。
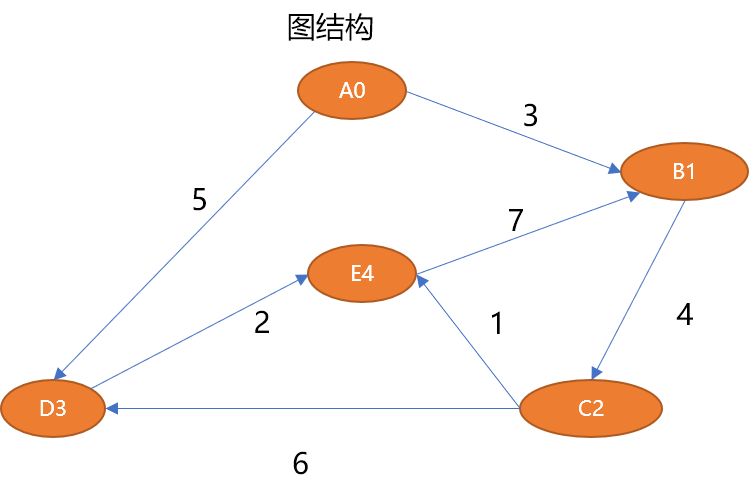
上記のグラフ構造は次のように説明できます。
# 5 个顶点
V={A0,B1,C2,D3,E4}
# 7 条边
E={ (A0,B1,3),(B1,C2,4),(C2,D3,6),(C2,E4,1),(D3,E4,2),(A0,D3,5),(E4,B1,7)}グラフの抽象データの説明グラフには少なくともいくつかのメソッドが必要です:
Graph (): 新しいグラフを作成するために使用されます。
add_vertex( vert ): 新しいノードをグラフに追加します。パラメータはノード タイプのオブジェクトである必要があります。
add_edge(fv,tv): 2 つのアイテム ポイント間のエッジ関係を確立します。
add_edge(fv,tv,w): 2 つのアイテム ポイント間にエッジを確立し、接続の重みを指定します。
find_vertex( key ): キーワード キーに基づいてグラフ内の頂点を検索します。
find_vertexs( ): すべての頂点情報をクエリします。
find_path(fv,tv): ある頂点から別の頂点までのパスを見つけます。
グラフ ストレージの実装には主に隣接行列とリンク リストの 2 種類があり、本記事では主に隣接行列について紹介します。
2 次元行列 (配列) を使用して、頂点間の関係を保存します。
たとえば、graph[5][5] は 5 つの頂点のリレーショナル データを格納できます。行番号と列番号は頂点を表します。行 v の交差するセル内のセルは、列 w の値は、頂点 v から頂点 w までのエッジの重みを表します。たとえば、grap[2][3]=6 は、C2 頂点と D3 頂点が接続されている (隣接している) ことを意味します。 、重みは 6
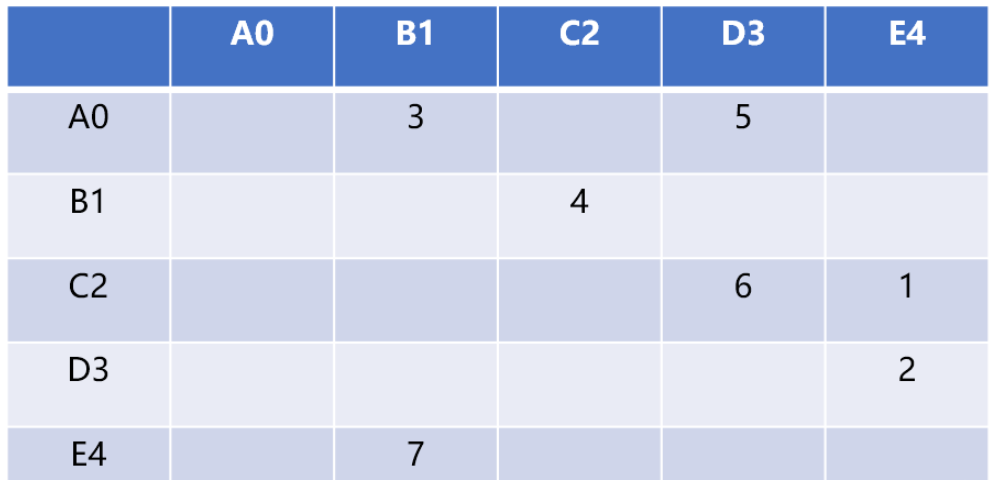
隣接行列の利点は、シンプルであり、どの頂点が接続されているかを明確に示すことができることです。すべての頂点のペアが接続されているわけではないため、行列には多くの未使用スペースがあり、これは「疎行列」と呼ばれることがよくあります。
マトリックスは、各頂点が他の頂点と関係がある場合にのみ塗りつぶされます。グラフ構造間の関係がそれほど複雑でない場合、この構造を使用してグラフ データを保存すると、多くのスペースが無駄になります。
隣接行列は、インターネット上の Web ページ間のリンクやソーシャル サークル内の人々間の社会的関係など、複雑な関係を持つグラフ構造を表現するのに適しています...2.2 隣接行列を実現するためのエンコーディング
"""
节（顶）点类
"""
class Vertex:
def __init__(self, name, v_id=0):
# 顶点的编号
self.v_id = v_id
# 顶点的名称
self.v_name = name
# 是否被访问过:False 没有 True:有
self.visited = False
# 自我显示
def __str__(self):
return '[编号为 {0}，名称为 {1} ] 的顶点'.format(self.v_id, self.v_name)
と v_name は理解しやすいです。なぜ visited を追加するのでしょうか? この変数は、検索計算の繰り返しを避けるために、パス検索プロセス中に頂点が検索されたかどうかを記録するために使用されます。
グラフ クラスには多くのメソッドがあります。ここではメソッドごとに紹介します。
初期化メソッドclass Graph:
"""
nums:相邻矩阵的大小
"""
def __init__(self, nums):
# 一维列表，保存节点，最多只能有 nums 个节点
self.vert_list = []
# 二维列表，存储顶点及顶点间的关系(权重)
# 初始权重为 0 ，表示节点与节点之间还没有建立起关系
self.matrix = [[0] * nums for _ in range(nums)]
# 顶点个数
self.v_nums = 0
# 使用队列模拟队列或栈，用于广度、深度优先搜索算法
self.queue_stack = []
# 保存搜索到的路径
self.searchPath = []
# 暂省略……
1 次元リスト
vert_list すべての頂点データを保存します。 2次元リスト
頂点間の関係データを保存します。
リストを使用して、後続の幅と深さの検索のためのキューまたはスタックをシミュレートします。
このリストには、
append() と pop() という 2 つの非常に貴重なメソッドがあります。
はリストにデータを追加するために使用され、毎回リストの末尾から追加されます。
デフォルトでは、リストの末尾からデータを削除してポップアップします。pop(parameter) 削除およびポップするインデックス値を指定できます。指定した位置からデータをアップします。 append() メソッドと Pop() メソッドを使用すると、スタックをシミュレートし、同じ場所からデータを入力および終了できます。
append() メソッドと Pop(0) メソッドを使用してキューをシミュレートし、後方からデータを追加し、前方からデータを取得します
searchPath: 使用されます広範な使用または深さ優先パス検索の結果を保存します。
上述方法注意一点，节点的编号由图内部逻辑提供，便于节点编号顺序的统一。 添加边方法 此方法是邻接矩阵表示法的核心逻辑。 添加边信息的方法有 2 个，一个用来添加无权重边，一个用来添加有权重的边。 查找某节点 使用线性查找法从节点集合中查找某一个节点。 查询所有节点 此方法仅为了查询方便。 查询节点之间的关系 测试代码： 在图中经常做的操作，就是查找从一个顶点到另一个顶点的路径。如怎么查找到 A0 到 E4 之间的路径长度： 从人的直观思维角度查找一下，可以找到如下路径： 在路径查找时，人的思维具有知识性和直观性特点，因此不存在所谓的尝试或碰壁问题。而计算机是试探性思维，就会出现这条路不通，再找另一条路的现象。 所以路径算法中常常会以错误为代价，在查找过程中会走一些弯路。常用的路径搜索算法有 2 种： 广度优先搜索 深度优先搜索 先看一下广度优先搜索的示意图： 广度优先搜索的基本思路： 确定出发点，本案例是 A0 顶点。 以出发点相邻的顶点为候选点，并存储至队列。 从队列中每拿出一个顶点后，再把与此顶点相邻的其它顶点做为候选点存储于队列。 不停重复上述过程，至到找到目标顶点或队列为空。 使用广度搜索到的路径与候选节点进入队列的先后顺序有关系。如第 1 步确定候选节点时 上图使用广度搜索可找到 其实 编码实现广度优先搜索： 广度优先搜索需要借助队列临时存储选节点，本文使用列表模拟队列。 在图类中实现广度优先搜索算法的方法： 广度优先搜索过程中，需要随时获取与当前节点相邻的节点， 测试广度优先搜索算法： 使用递归实现广度优先搜索算法： 先看一下深度优先算法的示意图。 深度优先搜索算法和广度优先搜索算法不同的地方在于：深度优先搜索算法将候选节点放在堆栈中。因栈是先进后出，所以，搜索到的节点顺序不一样。 使用循环实现深度优先搜索算法： 深度优先搜索算法需要用到栈，本文使用列表模拟。 测试： 使用递归实现深度优先搜索算法： 递归实现时，不需要使用全局栈，只需要获到当前节点的相邻节点便可。 以上がPython でグラフの幅と深さ優先のパス検索アルゴリズムを実装する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。 """
添加新顶点
"""
def add_vertex(self, vert):
if vert in self.vert_list:
# 已经存在
return
if self.v_nums >= len(self.matrix):
# 超过相邻矩阵所能存储的节点上限
return
# 顶点的编号内部生成
vert.v_id = self.v_nums
self.vert_list.append(vert)
# 数量增一
self.v_nums += 1 '''
添加节点与节点之间的边，
如果是无权重图，统一设定为 1
'''
def add_edge(self, from_v, to_v):
# 如果节点不存在
if from_v not in self.vert_list:
self.add_vertex(from_v)
if to_v not in self.vert_list:
self.add_vertex(to_v)
# from_v 节点的编号为行号，to_v 节点的编号为列号
self.matrix[from_v.v_id][to_v.v_id] = 1
'''
添加有权重的边
'''
def add_edge(self, from_v, to_v, weight):
# 如果节点不存在
if from_v not in self.vert_list:
self.add_vertex(from_v)
if to_v not in self.vert_list:
self.add_vertex(to_v)
# from_v 节点的编号为行号，to_v 节点的编号为列号
self.matrix[from_v.v_id][to_v.v_id] = weight '''
根据节点编号返回节点
'''
def find_vertex(self, v_id):
if v_id >= 0 or v_id <= self.v_nums:
# 节点编号必须存在
return [tmp_v for tmp_v in self.vert_list if tmp_v.v_id == v_id][0] '''
输出所有顶点信息
'''
def find_only_vertexes(self):
for tmp_v in self.vert_list:
print(tmp_v) '''
迭代节点与节点之间的关系（边）
'''
def find_vertexes(self):
for tmp_v in self.vert_list:
edges = self.matrix[tmp_v.v_id]
for col in range(len(edges)):
w = edges[col]
if w != 0:
print(tmp_v, '和', self.vert_list[col], '的权重为：', w)if __name__ == "__main__":
# 初始化图对象
g = Graph(5)
# 添加顶点
for _ in range(len(g.matrix)):
v_name = input("顶点的名称（ q 为退出）：")
if v_name == 'q':
break
v = Vertex(v_name)
g.add_vertex(v)
# 节点之间的关系
infos = [(0, 1, 3), (0, 3, 5), (1, 2, 4), (2, 3, 6), (2, 4, 1), (3, 4, 2), (4, 1, 7)]
for i in infos:
v = g.find_vertex(i[0])
v1 = g.find_vertex(i[1])
g.add_edge(v, v1, i[2])
# 输出顶点及边a
print("-----------顶点与顶点关系--------------")
g.find_vertexes()
'''
输出结果：
顶点的名称（ q 为退出）：A
顶点的名称（ q 为退出）：B
顶点的名称（ q 为退出）：C
顶点的名称（ q 为退出）：D
顶点的名称（ q 为退出）：E
[编号为 0，名称为 A ] 的顶点 和 [编号为 1，名称为 B ] 的顶点 的权重为： 3
[编号为 0，名称为 A ] 的顶点 和 [编号为 3，名称为 D ] 的顶点 的权重为： 5
[编号为 1，名称为 B ] 的顶点 和 [编号为 2，名称为 C ] 的顶点 的权重为： 4
[编号为 2，名称为 C ] 的顶点 和 [编号为 3，名称为 D ] 的顶点 的权重为： 6
[编号为 2，名称为 C ] 的顶点 和 [编号为 4，名称为 E ] 的顶点 的权重为： 1
[编号为 3，名称为 D ] 的顶点 和 [编号为 4，名称为 E ] 的顶点 的权重为： 2
[编号为 4，名称为 E ] 的顶点 和 [编号为 1，名称为 B ] 的顶点 的权重为： 7
'''3. 搜索路径
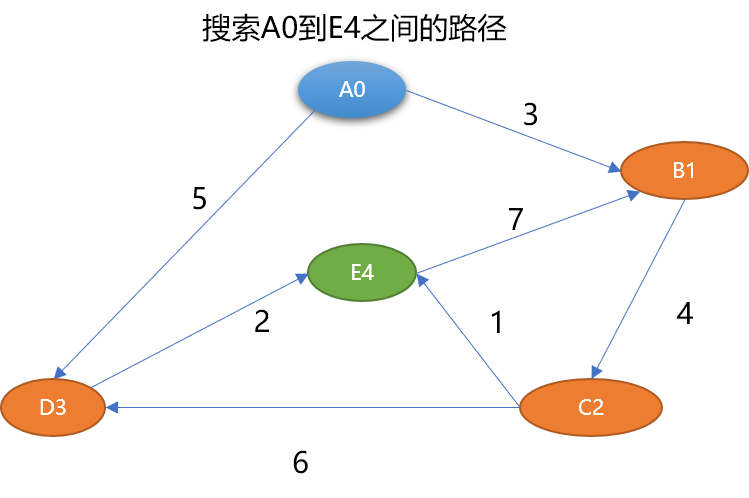
{A0，B1，C2，E4}路径长度为 8。{A0，D3，E4} 路径长度为 7。{A0，B1，C2，D3，E4} 路径长度为 15。3.1 广度优先搜索
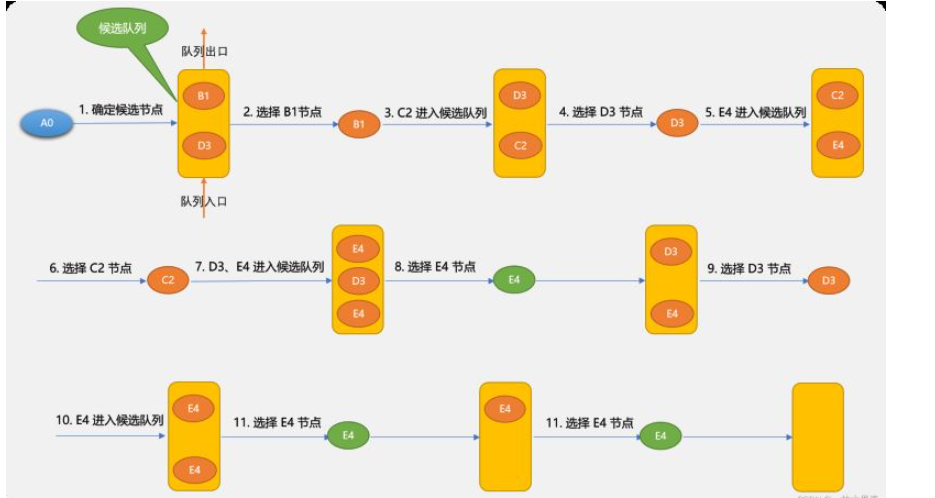
B1 和 D3 谁先进入队列，对于后面的查找也会有影响。A0~E4 路径是：{A0，B1，D3，C2，E4}{A0，B1，C2，E4} 也是一条有效路径，有可能搜索不出来，这里因为搜索到 B1 后不会马上搜索 C2，因为 B3 先于 C2 进入，广度优先搜索算法只能保证找到路径，而不能保存找到最佳路径。class Graph():
# 省略其它代码
'''
广度优先搜索算法
'''
def bfs(self, from_v, to_v):
# 查找与 fv 相邻的节点
self.find_neighbor(from_v)
# 临时路径
lst_path = [from_v]
# 重复条件：队列不为空
while len(self.queue_stack) != 0:
# 从队列中一个节点（模拟队列）
tmp_v = self.queue_stack.pop(0)
# 添加到列表中
lst_path.append(tmp_v)
# 是不是目标节点
if tmp_v.v_id == to_v.v_id:
self.searchPath.append(lst_path)
print('找到一条路径', [v_.v_id for v_ in lst_path])
lst_path.pop()
else:
self.find_neighbor(tmp_v)
'''
查找某一节点的相邻节点，并添加到队列（栈）中
'''
def find_neighbor(self, find_v):
if find_v.visited:
return
find_v.visited = True
# 找到保存 find_v 节点相邻节点的列表
lst = self.matrix[find_v.v_id]
for idx in range(len(lst)):
if lst[idx] != 0:
# 权重不为 0 ，可判断相邻
self.queue_stack.append(self.vert_list[idx])find_neighbor() 方法的作用就是用来把当前节点的相邻节点压入队列中。if __name__ == "__main__":
# 初始化图对象
g = Graph(5)
# 添加顶点
for _ in range(len(g.matrix)):
v_name = input("顶点的名称（ q 为退出）：")
if v_name == 'q':
break
v = Vertex(v_name)
g.add_vertex(v)
# 节点之间的关系
infos = [(0, 1, 3), (0, 3, 5), (1, 2, 4), (2, 3, 6), (2, 4, 1), (3, 4, 2), (4, 1, 7)]
for i in infos:
v = g.find_vertex(i[0])
v1 = g.find_vertex(i[1])
g.add_edge(v, v1, i[2])
print("----------- 广度优先路径搜索--------------")
f_v = g.find_vertex(0)
t_v = g.find_vertex(4)
g.bfs(f_v,t_v)
'''
输出结果
顶点的名称（ q 为退出）：A
顶点的名称（ q 为退出）：B
顶点的名称（ q 为退出）：C
顶点的名称（ q 为退出）：D
顶点的名称（ q 为退出）：E
----------- 广度优先路径搜索--------------
找到一条路径 [0, 1, 3, 2, 4]
找到一条路径 [0, 1, 3, 2, 3, 4]
''' '''
递归方式实现广度搜索
'''
def bfs_dg(self, from_v, to_v):
self.searchPath.append(from_v)
if from_v.v_id != to_v.v_id:
self.find_neighbor(from_v)
if len(self.queue_stack) != 0:
self.bfs_dg(self.queue_stack.pop(0), to_v)3.2 深度优先搜索算法
'''
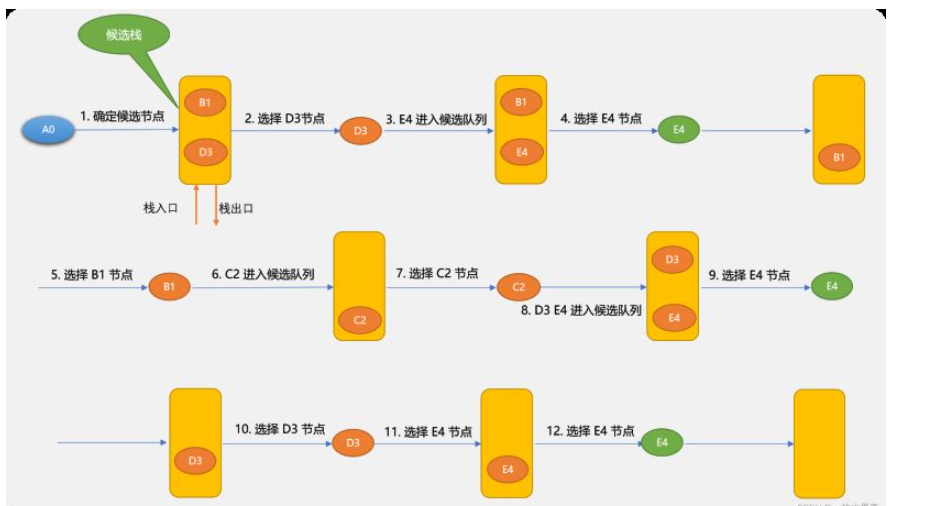
深度优先搜索算法
使用栈存储下一个需要查找的节点
'''
def dfs(self, from_v, to_v):
# 查找与 from_v 相邻的节点
self.find_neighbor(from_v)
# 临时路径
lst_path = [from_v]
# 重复条件：栈不为空
while len(self.queue_stack) != 0:
# 从栈中取一个节点（模拟栈）
tmp_v = self.queue_stack.pop()
# 添加到列表中
lst_path.append(tmp_v)
# 是不是目标节点
if tmp_v.v_id == to_v.v_id:
self.searchPath.append(lst_path)
print('找到一条路径:', [v_.v_id for v_ in lst_path])
lst_path.pop()
else:
self.find_neighbor(tmp_v)if __name__ == "__main__":
# 初始化图对象
g = Graph(5)
# 添加顶点
for _ in range(len(g.matrix)):
v_name = input("顶点的名称（ q 为退出）：")
if v_name == 'q':
break
v = Vertex(v_name)
g.add_vertex(v)
# 节点之间的关系
infos = [(0, 1, 3), (0, 3, 5), (1, 2, 4), (2, 3, 6), (2, 4, 1), (3, 4, 2), (4, 1, 7)]
for i in infos:
v = g.find_vertex(i[0])
v1 = g.find_vertex(i[1])
g.add_edge(v, v1, i[2])
# 输出顶点及边a
print("-----------顶点与顶点关系--------------")
g.find_vertexes()
print("----------- 深度优先路径搜索--------------")
f_v = g.find_vertex(0)
t_v = g.find_vertex(4)
g.dfs(f_v, t_v)
'''
输出结果
顶点的名称（ q 为退出）：A
顶点的名称（ q 为退出）：B
顶点的名称（ q 为退出）：C
顶点的名称（ q 为退出）：D
顶点的名称（ q 为退出）：E
-----------顶点与顶点关系--------------
[编号为 0，名称为 A ] 的顶点 和 [编号为 1，名称为 B ] 的顶点 的权重为： 3
[编号为 0，名称为 A ] 的顶点 和 [编号为 3，名称为 D ] 的顶点 的权重为： 5
[编号为 1，名称为 B ] 的顶点 和 [编号为 2，名称为 C ] 的顶点 的权重为： 4
[编号为 2，名称为 C ] 的顶点 和 [编号为 3，名称为 D ] 的顶点 的权重为： 6
[编号为 2，名称为 C ] 的顶点 和 [编号为 4，名称为 E ] 的顶点 的权重为： 1
[编号为 3，名称为 D ] 的顶点 和 [编号为 4，名称为 E ] 的顶点 的权重为： 2
[编号为 4，名称为 E ] 的顶点 和 [编号为 1，名称为 B ] 的顶点 的权重为： 7
----------- 深度优先路径搜索--------------
找到一条路径: [0, 3, 4]
找到一条路径: [0, 3, 1, 2, 4]
''' '''
递归实现深度搜索算法
'''
def def_dg(self, from_v, to_v):
self.searchPath.append(from_v)
if from_v.v_id != to_v.v_id:
# 查找与 from_v 节点相连的子节点
lst = self.find_neighbor_(from_v)
if lst is not None:
for tmp_v in lst[::-1]:
self.def_dg(tmp_v, to_v)
"""
查找某一节点的相邻节点，以列表方式返回
"""
def find_neighbor_(self, find_v):
if find_v.visited:
return
find_v.visited = True
# 查找与 find_v 节点相邻的节点
lst = self.matrix[find_v.v_id]
return [self.vert_list[idx] for idx in range(len(lst)) if lst[idx] != 0]
![[Web フロントエンド] Node.js クイック スタート](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
