
大規模モデルの出現における最も不思議な現象の 1 つは、思考のヒントの連鎖 (CoT) です。これは、特に数学的推論や意思決定の問題の解決において驚くべき結果を示しています。 CoTはどのくらい重要ですか?その成功の背後にあるメカニズムは何ですか?この記事では、北京大学の数名の研究者が、CoT が大規模言語モデル (LLM) 推論の実現に不可欠であることを証明し、理論的および実験的観点から CoT がどのように LLM の大きな可能性を解き放つことができるかを明らかにします。
最近の研究では、思考連鎖プロンプト (CoT) が、特に数学や推論を含む複雑な問題の処理において、大規模言語モデル (LLM) のパフォーマンスを大幅に向上させることができることがわかりました。しかし、多くの成功にもかかわらず、CoT の背後にあるメカニズムや LLM の可能性を引き出す方法は依然としてわかりにくいままです。
最近、北京大学の新しい研究により、CoT の背後にある謎が理論的な観点から明らかになりました。

論文リンク: https://arxiv.org/abs/2305.15408
Transformer に基づく大規模言語モデルは、自然言語処理の一般的なモデルとなり、さまざまなタスクで広く使用されています。主流の大規模モデルは、通常、自己回帰パラダイムに基づいて実装されており、具体的には、さまざまなタスク (テキスト翻訳、テキスト生成、質問応答など) を一律にシーケンス生成問題としてみなすことができ、質問と説明の入力が行われます。質問の回答は、プロンプト (プロンプト) と呼ばれる単語 (トークン) シーケンスにまとめてエンコードされ、質問に対する回答は、プロンプトに基づいて条件付きで後続の単語を生成するタスクに変換できます。


しかし、CoT は多数の実験で顕著なパフォーマンスを達成しましたが、その背後にある理論的メカニズムは依然として謎のままです。一方で、大規模なモデルには、数学や推論などに関する質問に直接答える上で、本質的な理論的欠陥が実際にあるのでしょうか?一方で、なぜ CoT はこれらのタスクに関する大規模モデルの機能を向上させることができるのでしょうか?この文書は、理論的な観点から上記の質問に答えます。
具体的には、研究者はモデル表現能力の観点から CoT を研究します。この記事では、数学的タスクと一般的な意思決定タスクについて、次の 2 つの表現能力における自己回帰に基づいて Transformer モデルを研究します。 (1) 回答を直接生成すること、(2) CoT を使用して完全なソリューション ステップを生成すること。
CoT は数学的問題を解決する鍵です。
大規模モデルの数学的機能を研究するために、この記事では、算術と方程式という 2 つの非常に基本的だが核となる数学的タスクを選択しました (次の図は、これら 2 つのタスクの入力の出力例を示しています) )。これらは複雑な数学的問題を解決するための基本的なコンポーネントであるため、これら 2 つの中心的な数学的問題を研究することで、一般的な数学的問題に対する大規模モデルの機能をより深く理解することができます。

研究者らはまず、Transformer が中間ステップを出力せずに上記の質問に対する回答を出力できるかどうかを調査しました。彼らは、現実と非常に一致する仮定を検討しました。つまり、対数精度の Transformer、つまり、Transformer の各ニューロンは、限られた精度 (精度は log n ビット) の浮動小数点数しか表現できません。ここで、n は最大長です。文の。この仮定は現実に非常に近いもので、たとえば GPT-3 では、マシン精度 (16 ビットまたは 32 ビット) は通常、出力文の最大長 (2048) よりもはるかに小さくなります。
この仮定の下で、研究者らは不可能な核心的な結果を証明しました: 定層と幅 d を持つ自己回帰 Transformer モデルの場合、直接出力が答えです非常に大きなモデル幅 d を使用して、上記の 2 つの数学的問題を解決することです。具体的には、入力長 n が増加するにつれて、d は多項式よりも大きくなる必要があります。
この結果の本質的な理由は、上記の 2 つの問題に対する効率的な並列アルゴリズムが存在しないため、典型的な並列モデルである Transformer ではそれらを解決できないことです。この記事では、理論コンピュータ科学における回路複雑性理論を使用して、上記の定理を厳密に証明しています。
では、モデルが答えを直接出力せず、中間導出ステップを上の図の形式で出力する場合はどうなるでしょうか?研究者らはさらに、モデルが中間ステップを出力できる場合、固定サイズ (入力長 n に依存しない) 自己回帰 Transformer モデルが上記の 2 つの数学的問題を解決できることを構築を通じて証明しました # 。
前の結果と比較すると、CoT を追加することで大規模モデルの表現力が大幅に向上することがわかります。研究者らはさらに、これについて直感的な理解を与えました。これは、CoT の導入により、生成された出力ワードが入力層に継続的にフィードバックされ、モデルの有効深さが大幅に増加し、CoT の出力長に比例するためです。したがって、Transformer の並列複雑性は大幅に改善されました。
CoT は一般的な意思決定の問題を解決する鍵です。研究者らは、数学的問題に加えて、一般的なタスクを解決する CoT の能力についてさらに検討しました。彼らは意思決定問題から出発して、動的計画法と呼ばれる、意思決定問題を解決するための一般的なフレームワークを検討しました。
ダイナミック プログラミング (DP) の基本的な考え方は、複雑な問題を、順番に解決できる一連の小規模なサブ問題に分解することです。問題を分解すると、さまざまなサブ問題間に重要な相互関係 (重複) があることが確認され、前のサブ問題の答えを使用して各サブ問題を効率的に解決できます。
最長昇順部分列 (LIS) と編集距離の解 (ED) は、書籍「アルゴリズム入門」で提案されている 2 つの有名な DP 問題です。次の表にこれらの集計を示します。状態空間の関数、2 つの問題に対する遷移関数。

研究者らは、自己回帰 Transformer モデルが次のような部分問題を解決できることを証明しました。このシーケンスは完全な動的計画思考の連鎖を出力するため、動的計画で解決できるすべてのタスクに対して正しい答えを出力できます。同様に、研究者らは生成的思考連鎖が必要であることをさらに実証しました。多くの難しい動的計画問題では、定層の多項式サイズの Transformer モデルは正しい答えを直接出力できません。この記事では、文脈自由文法のメンバーシップ テストの問題に対する反例を示しています。
実験
研究者らは最終的に、算術式の評価、一次方程式の解法、最長上昇部分列の解法という 4 つの異なるタスクを考慮して、上記の理論を検証するために多数の実験を設計しました。編集距離を解決します。実験結果は、CoT データを使用してトレーニングすると、3 層の自己回帰 Transformer モデルがすべてのタスクでほぼ完璧なパフォーマンスを達成できることを示しています。ただし、正しい答えを直接出力すると、すべてのタスクで (より深いモデルを使用した場合でも) パフォーマンスが低下します。この結果は、さまざまな複雑なタスクを解決する自己回帰トランスフォーマーの能力を明確に示しており、これらのタスクを解決する際の CoT の重要性を示しています。 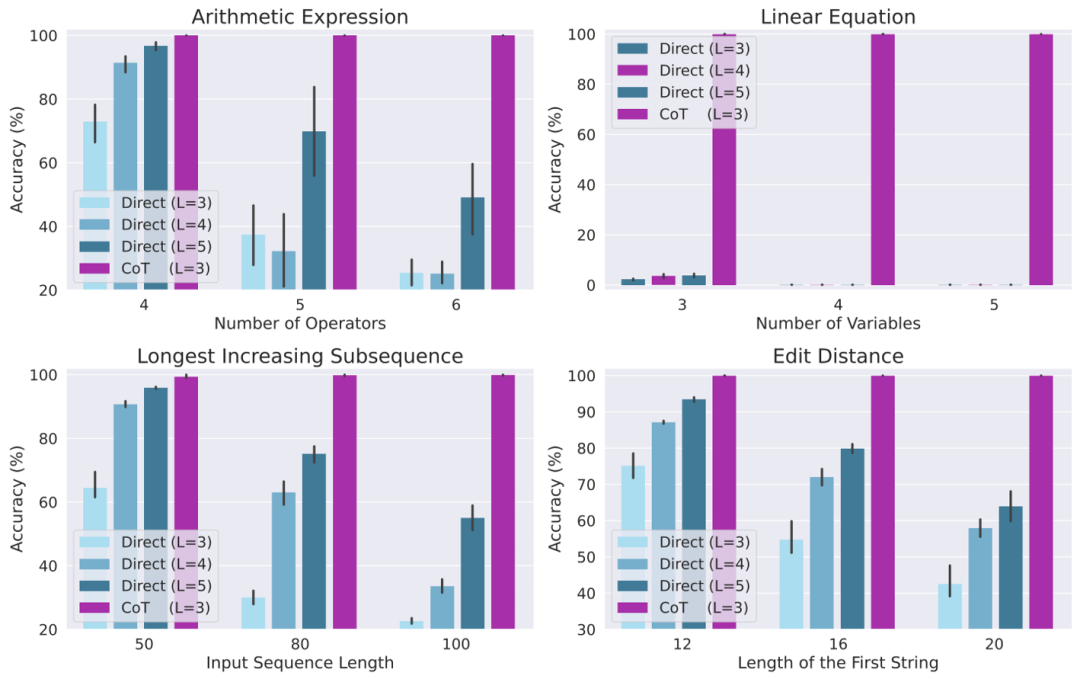
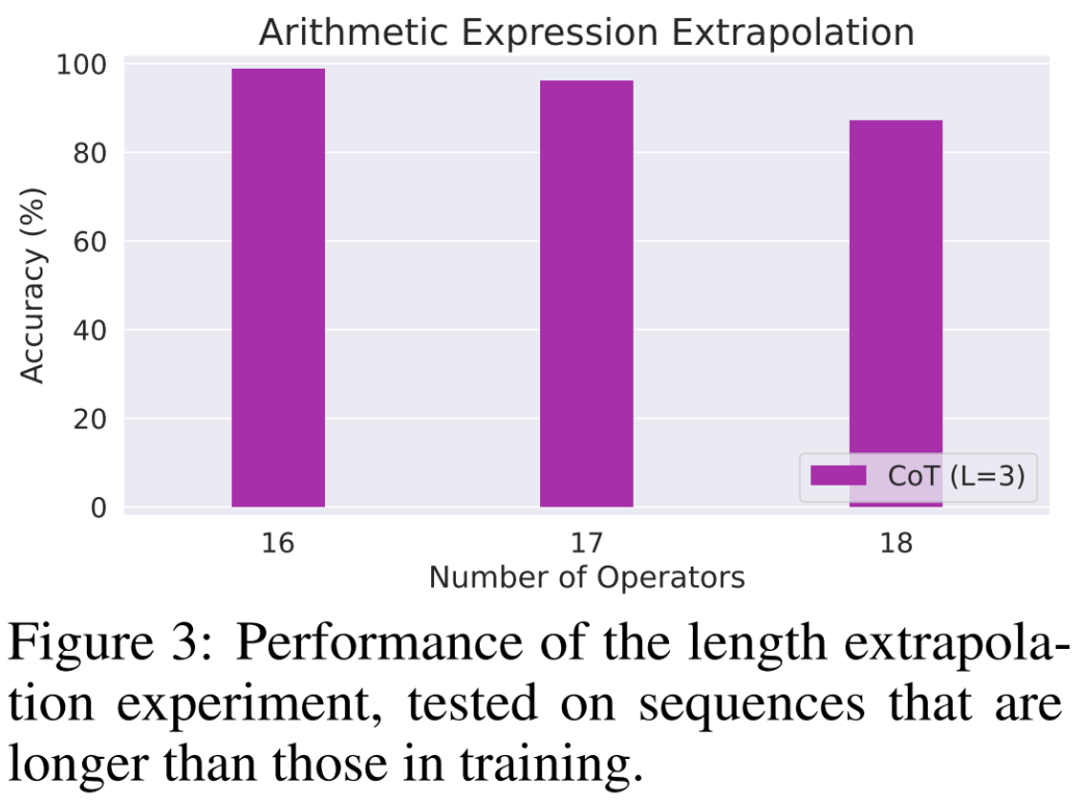
以上が思考の連鎖はどのようにして言語モデルの隠された機能を解放するのでしょうか?最新の理論研究でその背後にある謎が明らかにの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。