HTML5 の Canvas_html5 チュートリアルのヒントを使用して曲線を描く簡単な方法

Canvas2D 付属のカーブメソッド
最近、3D ソフトボディの計算を勉強しているので、少しずつ知識をキャッチアップしようとしています。多くの場合、数値解析、主に曲線のさまざまな補間アルゴリズムが含まれます。突然、Canvas2D 自体も 2 次および 3 次ベジェ曲線を使用して曲線を描くことができることを思い出しました。実際、私はこの方法を使ったことがないので、今すぐ試してみましょう~
この記事では単純な曲線の描画についてのみ説明し、多くの複雑な原理については説明しません。なお、ベジェ曲線の原理はWikipediaを見れば分かります。実際、描画ツールの多くの単純な曲線描画ではベジェ曲線が使用されています。Windows に付属の描画ツールで曲線を使用したことがある場合は、ベジェ曲線に精通しているはずです。まず直線をドラッグしてから、特定の位置をクリックして直線を変形させることができます。最初のドラッグ操作では曲線の 2 つの頂点を決定し、クリック操作では中間点を追加します。 Windows に付属の描画ツールは 3 次ベジェ曲線を使用しており、中間点を 2 つ追加できます。ベジェ曲線は一般的な多項式補間とは異なり、その中点は曲線が通過する必要がある頂点ではなく、制御点としてのみ使用されます。閉じた曲線も作成できます。 Canvas2D には、曲線を描画するための 2 つのメソッドが用意されています。
quadraticCurveTo: 2 次ベジェ曲線
bezierCurveTo: 3 次ベジェ曲線
現在の位置から線を描画します。 moveTo メソッドを使用して、現在位置を指定できます。曲線の開始位置を取得したら、中間点と終了位置も必要になります。これらの位置座標を描画関数に渡すだけです。たとえば、2次ベジェ曲線には中間点と終了位置が必要なので、2つの座標をquadraticCurveTo関数に渡す必要があります。座標は x と y で構成されます。つまり、この関数には 4 つのパラメーターがあることになります。 bezierCurveTo は、2 つの中間点があることを除いて同じです。以下で使ってみましょう

CSS コードコンテンツをクリップボードにコピーします

1. <キャンバス ID="キャンバス" 幅=" 200" 高さ="200"></canvas>
2. <スクリプト
3. var g=canvas.getContext("2d");
//普通の直線
g.beginPath();
g.ストロークスタイル=
6. "#CCC"; g.moveTo(0,0);
7. g.lineTo(200,0);
8. g.lineTo(0,200);
9. g.lineTo(200,200);
10. g.ストローク()
11. //ベズカーブ
12. g.beginPath();
13. g.ストロークスタイル=
"#F00"
14. ; g.moveTo(0,0);
g.bezierCurveTo(200,0, 0,200, 200,200);
15. g.ストローク()
16. </script>
18. Z 字の軌跡に従って 4 つの点を与え、通常の直線とベジェ曲線を描きます。これは単なる普通の曲線です。ベジェ曲線の優れた点は、このコード
のような閉じた曲線を描画できることです。

CSS コード

コンテンツをクリップボードにコピーします

g.beginPath();

g.ストロークスタイル=
1. "#00F";
g.moveTo(100,0);
2. g.bezierCurveTo(-100,200, 300,200, 100,0); g.ストローク()

3. 

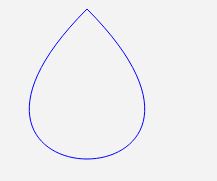
   3次ベジェ曲線の開始位置と終了位置を同じ点に設定し、閉曲線を描きます。ベジェ曲線の補間方向は座標軸に従わないため、閉曲線を描くことができます。多項式補間で閉曲線を描きたい場合は、パラメータを変換し、極座標系を使用して完成させる必要があります。
   私が使用する例はすべて 3 次ベジェ曲線です。実は2段目も同じなのですが、中間点がないと思い通りの絵が描けません。あまり詳しくは述べませんので、この記事はここまでです = =。 。