こっそりコンピューターの基礎をいくつか見てみたのですが、これから Java を学ぶのは不正行為のようなものです。

Javaを学ぶ前に質問したいのですが、コンピュータの基礎を学ぶ必要があると思いますか?

そんなつまらない基礎知識を読む必要はないと思う人も多いと思いますが、HelloWorld から直接始めたほうが良いでしょう。まずはプログラムを触って印象を掴み、コードが動くようにして、徐々に進めていきましょう。プログラムの文法を深く学び、最終的には実際に使えるようになるプログラム構築プロジェクト、つまり実践的な学習方法です。

まず、この学習方法を否定するものではありません。確かに一部の学生、特に就職に不安を抱えている学生にとっては、むしろこの方法の方が適しています。まずは使い方を学んでください。原理としては、後でゆっくりと学んでください。結局のところ、パンよりも重要なものはありませんか?

しかし、対数をゼロから学習している生徒には、プログラミングの考え方や常識を理解するために、コンピューターの基礎知識から始めることをお勧めします。これは、将来の学習にも非常に役立ちます。家を建てるのと同じで、茅葺きの家を建てる人もいるし、土の家を建てる人もいるし、二階建ての洋風の家を建てたい人もいる。基礎の深さは、将来の成果のレベルに直接影響します。

それでは、コンピューターの基本的な知識を簡単に理解しましょう。

1. 機械語の分類

機械語

機械語とは、コンピュータが直接認識できる言語です。これは、バイナリ コード命令で直接表現されるコンピュータ言語です。一定の桁数の0と1の列で構成されるコードがいくつかのセグメントに分かれており、各セグメントのコードは異なる意味を表します。たとえば、次は単純なマシン コードの文字列です。

010100100000  // 520

多くの人が、なぜマシン コードは 0 と 1 で構成されているのかと尋ねます。

マシンコードはプログラム命令に応答するためにコンピューターハードウェアを制御する必要があるため、0は低電位を表し、1は高電位を表し、スイッチを制御するのと同じ論理回路を生成できます。 0 はクローズ、1 はオープンです。

アセンブリ言語

アセンブリ言語は開発者向けの言語であり、機械語はすべて0と1であるため、開発者が直接制御して使用することは困難ですが、一部の特殊記号はバイナリ コードのマーカーとして使用する必要があります。開発者はこれらの特殊記号を入力して命令の発行を完了し、コンピューターに代わって動作させます。これらの特殊記号はアセンブリ言語です。コンピュータはアセンブリ言語を直接認識することができないため、アセンブリ言語を機械語に翻訳するソフトウェアが必要です。機械語との違いは命令の表現方法にあり、アセンブリ言語の本体はアセンブリ命令であり、機械語に比べてプログラマにとって覚えやすい言語です。

MOV AX,1234H  //汇编指令: 寄存器AX的内容送到1234H中
101110000011010000010010 //机器指令

高級言語

高級言語は、c、c、java、python、php などのものが一般的です。

私たちの通常の思考に近く、コードが書きやすく、読みやすいのが最大の特徴です。同じ機能を実現するのに、高級言語を使用する時間が短縮され、プログラムコードが短くなり、読みやすくなります。第 2 に、高級言語は移植可能です。つまり、コードをほとんど、またはまったく変更せずに、さまざまな種類のコンピューター上で実行できます。

print('Hello World')   // python版HelloWorld

我们从这个程序可以看出来，高级语言屏蔽了机器内部指令运行细节，我们可以像写作一样书写程序，而不用关心语言内部的实现细节，这大大提高了我们的开发效率，节约开发成本。

当然，其缺点也很明显，使用高级语言编写的程序运行时，需要先将其翻译成低级语言计算机才能运行它，在翻译过程中可能会产生一些多余的部分，运行效率低些。另外，对硬件的可控性相对于低级语言弱些，目标代码量较大。

二. 进制

推荐使用在线工具进行进制转换：

https://tool.oschina.net/hexconvert/

二进制

由数字0和1组成，逢二进一，比如机器码就是二进制的，是最简单的计算机可读懂的代码，例如 0101（表示十进制数字5）。

八进制

由1到7组成的数字串，数字最大不会超过7，逢八进一，例如 157(表示十进制数字111)

十进制

我们日常使用的数字都是十进制类型的，逢十进一，例如 0123456789。

十六进制

由1到9，a-f（或者是A-F，分别代表10-15）组成的数字串，数字最大不会超过15，其中字母是不区分大小写的，逢十六进一，例如0F83（表示十进制数3971）

进制转换

1. K进制与十进制数的转换

假设有一个n+1位的K进制数，它的形式如下：

AnAn-1…A3A2A1A0
则它的大小为：（也就是对应的我们能看懂的十进制数为）

A0 * K^0 + A1 * K^1....+ An * K^n      //K^n表示K的n次方

二进制数：10101 转换成 十进制数为：21

 1*2^4 + 0*2^3 + 1*2^2 + 0*2^1+1*2^0 = 21

2. 十进制与k进制的转换

短除法。

举个栗子：

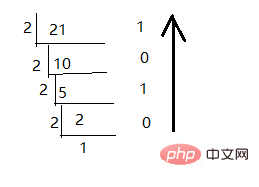
从图可以看出，用十进制数21一直除以2，每次得到的余数倒数就是最后的二进制数10101。同样，十进制转八进制、十进制转十六进制都是一样的套路，非常简单。

3. 二进制与八进制和十六进制之间转换

8是2的3次方，16是2的4次方，所以这之间的转换存在一种快捷方法。以2转8示例，将2进制从低位到高位，每3个一组，如果是十六进制就每4个一组，高位不足3位的补0，然后将每组依次转换成对应的十进制，得到的结果就是对应的8进制或者16进制。

二进制10101100101转八进制：2545

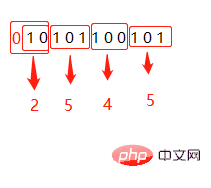
二进制10101100101转十六进制：565

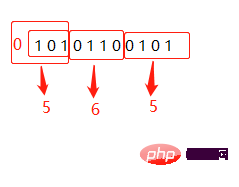
三. 原码、反码、补码

在计算机中，最小的单位是位，也称为比特（bit）。而另一个常用单位是字节，一个字节是8位，也就是8比特，所以我们常用的二进制表示法是8位。

原码

原码是一种非常常见的二进制表示形式。在原码中，为了区别正数和负数，将二进制中的最高位作为符号位，如果是0表示正数，如果是1表示负数。

举个栗子：

0000 0001   // 表示 1
1000 0001   // 表示 -1

反码

不知道大家有没有注意到原码的一个问题，那就是负数参与计算的时候，比如

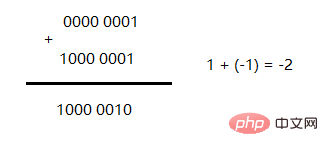
出现了一个大问题，就是1 + (-1) 不等于0，而等于 -2。

这可咋整？

この問題を解決するために、賢いコンピューターの先人たちはリバースコーディングを考えました。元のコードを逆コードに変換するための規則は次のとおりです。 正の数の逆コードはそれ自体であり、負の数の逆コードは符号ビットは変更されず、他のビットは反転されます。 否定の法則は、0 の場合は 1 になり、1 の場合は 0 になります。
逆コードに変換する計算を見てみましょう:

得られた結果は 1111 1111 です。

ねえ?これは間違っています、なぜ 0 ではないのですか?

これは逆コードの計算結果ですので、心配しないでください。逆コードを元のコード 1111 1111 —> 1000 0000 に変換すると、0 である -0 が得られます。期待された結果と完全に一致し、元のコードの計算問題が解決されました。

#補数コード

補数コードは負の数の計算の問題を解決しますが、まだ解決されていない問題が 1 つあります。解決済み、つまり -0 です。負の数の最上位ビットの符号ビットの存在により、元の 8 ビットの 2 進数は 2 の 8 乗、つまり 256 個の数を表現できますが、元のコードと補数コードを使用すると、それしか表現できません。は 255 を表しますが、これは私たちにとって非常に不快なものです。では、この足りない数字を補うにはどうすればよいでしょうか?

ハゲプログラマーたちは、対応する解決策、つまりコード補完も考え出しました。

元のコードを補数コードに変換するための規則:

正の数の補数コードはそのまま、負の数の補数コードは、符号ビットは変更されず、残りの桁が反転されます(つまり、補数コードになります) に 1 を追加します。

例:

元のコード: 0000 0001、補数コード: 0000 0001

元のコード: 1000 0001、補数コード: 1111 1111

計算:

#上記からわかるように、補数計算を使用すると (-0 ではなく) 0 が得られ、数値が 1 つ減る問題が解決されます。

補数コードでは、0は0000 0000、1000 0000は-128と表記されていますが、これは規則です。

注意事項

1. 1 の補数と 1 の補数を直接使用して 2 進数を 10 進数に変換することはできません。対応するサイズを対応する 10 進法に変換するには、まず元のコードに変換する必要があります。つまり、元のコードはサイズに直接関係する表現形式です。

2. コンピューター システムでは、値は常に補数の形式で表現され、格納されます。コード

3. 元のコード、正の数の補数と補数は同じです

4. 負の数の元のコードは反転されます。符号ビットは変更されず、

5. 負の数は補数に変換されます: 符号ビットは変更されず、残りのビットは反転されてから 1 を加えます

6. 負の数は補数に補われます。符号ビットは変更されず、残りのビットは 1 つ減ります。

7. 負の数は元の数に変換されます。符号ビットは変更されません。残りのビットは 1 つ減らされて反転されます。

以上がこっそりコンピューターの基礎をいくつか見てみたのですが、これから Java を学ぶのは不正行為のようなものです。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。