
# データ構造とアルゴリズムは Linux カーネル コードで広く使用されており、最もよく使用される 2 つはリンク リストと赤黒ツリーです。
Linux カーネル コードは、リンク リスト データ構造を広範囲に利用します。リンクリストは、配列を動的に展開できないという問題を解決するために作成されたデータ構造です。リンクされたリストに含まれる要素は、動的に作成、挿入、削除できます。リンクされたリストの各要素は個別に保存されるため、連続したメモリを占有する必要はありません。リンク リストは通常、複数のノードで構成され、各ノードの構造は同じで、有効データ領域とポインタ領域の 2 つの部分で構成されます。有効データ領域は有効データ情報を格納するために使用され、ポインタ領域はリンクリストの先行ノードまたは後続ノードを指すために使用されます。したがって、リンク リストは、ポインタを使用してノードを直列に接続する記憶構造です。
(1) 一方向リンクリスト
一方向リンクリストのポインタ領域には次のノードへのポインタのみが含まれるため、単一の-direction リンクリストは次のように形成されます。コードを示します。
struct list {
int data; /*有效数据*/
struct list *next; /*指向下一个元素的指针*/
};図に示すように、一方向リンク リストには一方向のモビリティがあります。つまり、現在のノードの後続ノードにのみアクセスできますが、現在のノードの先行ノードにはアクセスできません。なので、実際のプロジェクトで使用できます。
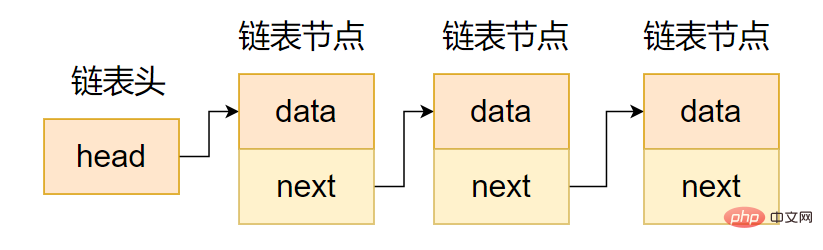
一方向連鎖表現意図
(2) 二重連結リスト
図のように、二重リンク リストと一方向リンク リストの違いは、次のコードに示すように、ポインター領域に 2 つのポインターが含まれ、1 つは先行ノードを指し、もう 1 つは後続ノードを指すことです。
struct list {
int data; /*有效数据*/
struct list *next; /*指向下一个元素的指针*/
struct list *prev; /*指向上一个元素的指针*/
};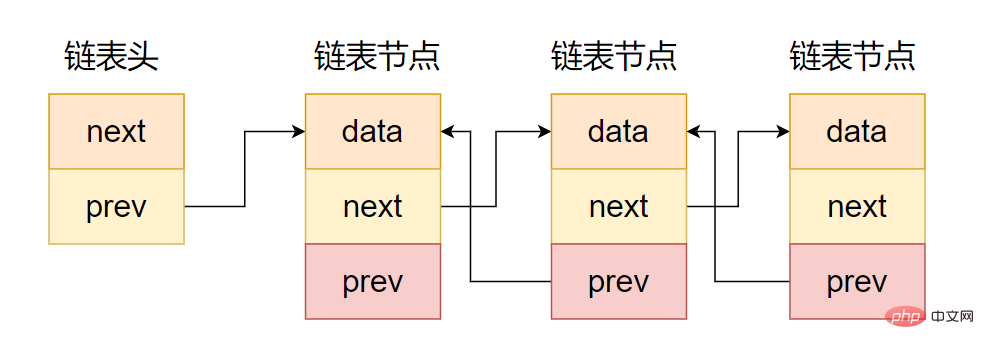
双方向チェーン表現の意図
(3)Linuxカーネルリンクリスト実装
One- way リンクリストと双方向リンクリスト データ領域が固定データである必要があるなど、実際に使用する際にはいくつかの制限がありますが、実際のニーズは多様です。異なるデータ領域ごとにリンク リストのセットが必要となるため、この方法ではリンク リストのユニバーサル セットを構築できません。この目的を達成するために、Linux カーネルはすべてのリンク リスト操作メソッドの共通部分を抽出し、異なる部分はコード プログラマに任せます。 Linux カーネルは、純粋なリンク リスト カプセル化のセットを実装しています。リンク リスト ノード データ構造には、ポインタ領域のみがあり、データ領域はありません。また、ノード関数の作成、ノード関数の挿入、ノード関数の削除、ノード関数のトラバースなど、さまざまな操作関数もカプセル化されています。ノード機能など
Linux カーネルのリンク リストは、struct list_head データ構造を使用して記述されます。
<include/linux/types.h>
struct list_head {
struct list_head *next, *prev;
};struct list_head数据结构不包含链表节点的数据区,通常是嵌入其他数据结构,如struct page数据结构中嵌入了一个lru链表节点,通常是把page数据结构挂入LRU链表。
<include/linux/mm_types.h>
struct page {
...
struct list_head lru;
...
}链表头的初始化有两种方法,一种是静态初始化,另一种动态初始化。
把next和prev指针都初始化并指向自己,这样便初始化了一个带头节点的空链表。
<include/linux/list.h>
/*静态初始化*/
#define LIST_HEAD_INIT(name) { &(name), &(name) }
#define LIST_HEAD(name) \
struct list_head name = LIST_HEAD_INIT(name)
/*动态初始化*/
static inline void INIT_LIST_HEAD(struct list_head *list)
{
list->next = list;
list->prev = list;
}添加节点到一个链表中,内核提供了几个接口函数,如list_add()是把一个节点添加到表头,list_add_tail()是插入表尾。
<include/linux/list.h> void list_add(struct list_head *new, struct list_head *head) list_add_tail(struct list_head *new, struct list_head *head)
遍历节点的接口函数。
#define list_for_each(pos, head) \ for (pos = (head)->next; pos != (head); pos = pos->next)
这个宏只是遍历一个一个节点的当前位置,那么如何获取节点本身的数据结构呢?这里还需要使用list_entry()宏。
#define list_entry(ptr, type, member) \
container_of(ptr, type, member)
container_of()宏的定义在kernel.h头文件中。
#define container_of(ptr, type, member) ({ \
const typeof( ((type *)0)->member ) *__mptr = (ptr); \
(type *)( (char *)__mptr - offsetof(type,member) );})
#define offsetof(TYPE, MEMBER) ((size_t) &((TYPE *)0)->MEMBER)其中offsetof()宏是通过把0地址转换为type类型的指针,然后去获取该结构体中member成员的指针,也就是获取了member在type结构体中的偏移量。最后用指针ptr减去offset,就得到type结构体的真实地址了。
下面是遍历链表的一个例子。
<drivers/block/osdblk.c>
static ssize_t class_osdblk_list(struct class *c,
struct class_attribute *attr,
char *data)
{
int n = 0;
struct list_head *tmp;
list_for_each(tmp, &osdblkdev_list) {
struct osdblk_device *osdev;
osdev = list_entry(tmp, struct osdblk_device, node);
n += sprintf(data+n, "%d %d %llu %llu %s\n",
osdev->id,
osdev->major,
osdev->obj.partition,
osdev->obj.id,
osdev->osd_path);
}
return n;
}红黑树(Red Black Tree)被广泛应用在内核的内存管理和进程调度中,用于将排序的元素组织到树中。红黑树被广泛应用在计算机科学的各个领域中,它在速度和实现复杂度之间提供一个很好的平衡。
红黑树是具有以下特征的二叉树。
每个节点或红或黑。
红黑树的一个优点是,所有重要的操作(例如插入、删除、搜索)都可以在O(log n)时间内完成,n为树中元素的数目。经典的算法教科书都会讲解红黑树的实现,这里只是列出一个内核中使用红黑树的例子,供读者在实际的驱动和内核编程中参考。这个例子可以在内核代码的documentation/Rbtree.txt文件中找到。
#include <linux/init.h>
#include <linux/list.h>
#include <linux/module.h>
#include <linux/kernel.h>
#include <linux/slab.h>
#include <linux/mm.h>
#include <linux/rbtree.h>
MODULE_AUTHOR("figo.zhang");
MODULE_DESCRIPTION(" ");
MODULE_LICENSE("GPL");
struct mytype {
struct rb_node node;
int key;
};
/*红黑树根节点*/
struct rb_root mytree = RB_ROOT;
/*根据key来查找节点*/
struct mytype *my_search(struct rb_root *root, int new)
{
struct rb_node *node = root->rb_node;
while (node) {
struct mytype *data = container_of(node, struct mytype, node);
if (data->key > new)
node = node->rb_left;
else if (data->key < new)
node = node->rb_right;
else
return data;
}
return NULL;
}
/*插入一个元素到红黑树中*/
int my_insert(struct rb_root *root, struct mytype *data)
{
struct rb_node **new = &(root->rb_node), *parent=NULL;
/* 寻找可以添加新节点的地方 */
while (*new) {
struct mytype *this = container_of(*new, struct mytype, node);
parent = *new;
if (this->key > data->key)
new = &((*new)->rb_left);
else if (this->key < data->key) {
new = &((*new)->rb_right);
} else
return -1;
}
/* 添加一个新节点 */
rb_link_node(&data->node, parent, new);
rb_insert_color(&data->node, root);
return 0;
}
static int __init my_init(void)
{
int i;
struct mytype *data;
struct rb_node *node;
/*插入元素*/
for (i =0; i < 20; i+=2) {
data = kmalloc(sizeof(struct mytype), GFP_KERNEL);
data->key = i;
my_insert(&mytree, data);
}
/*遍历红黑树,打印所有节点的key值*/
for (node = rb_first(&mytree); node; node = rb_next(node))
printk("key=%d\n", rb_entry(node, struct mytype, node)->key);
return 0;
}
static void __exit my_exit(void)
{
struct mytype *data;
struct rb_node *node;
for (node = rb_first(&mytree); node; node = rb_next(node)) {
data = rb_entry(node, struct mytype, node);
if (data) {
rb_erase(&data->node, &mytree);
kfree(data);
}
}
}
module_init(my_init);
module_exit(my_exit);mytree是红黑树的根节点,my_insert()实现插入一个元素到红黑树中,my_search()根据key来查找节点。内核大量使用红黑树,如虚拟地址空间VMA的管理。
生产者和消费者模型是计算机编程中最常见的一种模型。生产者产生数据,而消费者消耗数据,如一个网络设备,硬件设备接收网络包,然后应用程序读取网络包。环形缓冲区是实现生产者和消费者模型的经典算法。环形缓冲区通常有一个读指针和一个写指针。读指针指向环形缓冲区中可读的数据,写指针指向环形缓冲区可写的数据。通过移动读指针和写指针实现缓冲区数据的读取和写入。
在Linux内核中,KFIFO是采用无锁环形缓冲区的实现。FIFO的全称是“First In First Out”,即先进先出的数据结构,它采用环形缓冲区的方法来实现,并提供一个无边界的字节流服务。采用环形缓冲区的好处是,当一个数据元素被消耗之后,其余数据元素不需要移动其存储位置,从而减少复制,提高效率。
(1)创建KFIFO
在使用KFIFO之前需要进行初始化,这里有静态初始化和动态初始化两种方式。
<include/linux/kfifo.h> int kfifo_alloc(fifo, size, gfp_mask)
该函数创建并分配一个大小为size的KFIFO环形缓冲区。第一个参数fifo是指向该环形缓冲区的struct kfifo数据结构;第二个参数size是指定缓冲区元素的数量;第三个参数gfp_mask表示分配KFIFO元素使用的分配掩码。
静态分配可以使用如下的宏。
#define DEFINE_KFIFO(fifo, type, size) #define INIT_KFIFO(fifo)
(2)入列
把数据写入KFIFO环形缓冲区可以使用kfifo_in()函数接口。
int kfifo_in(fifo, buf, n)
该函数把buf指针指向的n个数据复制到KFIFO环形缓冲区中。第一个参数fifo指的是KFIFO环形缓冲区;第二个参数buf指向要复制的数据的buffer;第三个数据是要复制数据元素的数量。
(3)出列
从KFIFO环形缓冲区中列出或者摘取数据可以使用kfifo_out()函数接口。
#define kfifo_out(fifo, buf, n)
该函数是从fifo指向的环形缓冲区中复制n个数据元素到buf指向的缓冲区中。如果KFIFO环形缓冲区的数据元素小于n个,那么复制出去的数据元素小于n个。
(4)获取缓冲区大小
KFIFO提供了几个接口函数来查询环形缓冲区的状态。
#define kfifo_size(fifo) #define kfifo_len(fifo) #define kfifo_is_empty(fifo) #define kfifo_is_full(fifo)
kfifo_size()用来获取环形缓冲区的大小,也就是最大可以容纳多少个数据元素。kfifo_len()用来获取当前环形缓冲区中有多少个有效数据元素。kfifo_is_empty()判断环形缓冲区是否为空。kfifo_is_full()判断环形缓冲区是否为满。
(5)与用户空间数据交互
KFIFO还封装了两个函数与用户空间数据交互。
#define kfifo_from_user(fifo, from, len, copied) #define kfifo_to_user(fifo, to, len, copied)
kfifo_from_user()是把from指向的用户空间的len个数据元素复制到KFIFO中,最后一个参数copied表示成功复制了几个数据元素。
kfifo_to_user()逆に、KFIFO のデータ要素をユーザー空間にコピーします。これら 2 つのマクロは、copy_to_user()、copy_from_user()、および KFIFO メカニズムを組み合わせて、ドライバー開発者に利便性を提供します。
以上がLinux カーネルで一般的に使用されるデータ構造とアルゴリズムの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。