Java でのメモ化 (1D、2D、および 3D) 動的プログラミング
メモ化は、提供された入力の結果 (配列に格納) を記録することで、同じ入力セットに対してメソッドが複数回実行されないようにし、再帰的アルゴリズムのパフォーマンスを向上させるために使用される動的プログラミングに基づく手法です。 。メモ化は、再帰的メソッドを実装するトップダウンのアプローチを通じて実現できます。
基本的なフィボナッチ数列の例を通じて、この状況を理解しましょう。
1-D メモ化
非定数パラメーターが 1 つだけ (1 つのパラメーターの値のみが変更される) を持つ再帰的アルゴリズムを検討します。そのため、このメソッドは 1-D メモ化 と呼ばれます。次のコードは、フィボナッチ数列の N 番目 (N までのすべての項) を見つけるためのものです。
例
public int fibonacci(int n) {
if (n == 0)
return 0;
if (n == 1)
return 1;
System.out.println("Calculating fibonacci number for: " + n);
return (fibonacci(n - 1) + fibonacci(n - 2));
}出力
上記のコードをn=5で実行すると、次の出力が生成されます。
Calculating fibonacci number for: 5 Calculating fibonacci number for: 4 Calculating fibonacci number for: 3 Calculating fibonacci number for: 2 Calculating fibonacci number for: 2 Calculating fibonacci number for: 3 Calculating fibonacci number for: 2
n=5 のフィボナッチ値は次のとおりです: 5
2 と 3 のフィボナッチ数は複数回計算されることに注意してください。条件 n=5 について上記の再帰ツリーを描いて、よりよく理解してみましょう。
ノードの 2 つの子ノードは、ノードが行う再帰呼び出しを表します。 F(3) と F(2) が複数回計算されていることがわかりますが、各ステップの後に結果をキャッシュすることで計算を回避できます。
インスタンス変数 memoize Set を使用して結果をキャッシュします。まず n が memoize Set に既に存在するかどうかを確認し、存在する場合は値を返し、存在しない場合は値を計算してセットに追加します。
例
import java.util.HashMap;
import java.util.Map;
public class TutorialPoint {
private Map<Integer, Integer> memoizeSet = new HashMap<>(); // O(1)
public int fibMemoize(int input) {
if (input == 0)
return 0;
if (input == 1)
return 1;
if (this.memoizeSet.containsKey(input)) {
System.out.println("Getting value from computed result for " + input);
return this.memoizeSet.get(input);
}
int result = fibMemoize(input - 1) + fibMemoize(input - 2);
System.out.println("Putting result in cache for " + input);
this.memoizeSet.put(input, result);
return result;
}
public int fibonacci(int n) {
if (n == 0)
return 0;
if (n == 1)
return 1;
System.out.println("Calculating fibonacci number for: " + n);
return (fibonacci(n - 1) + fibonacci(n - 2));
}
public static void main(String[] args) {
TutorialPoint tutorialPoint = new TutorialPoint();
System.out.println("Fibonacci value for n=5: " + tutorialPoint.fibMemoize(5));
}
}出力
上記のコードを実行すると、次の出力が生成されます
Adding result in memoizeSet for 2 Adding result in memoizeSet for 3 Getting value from computed result for 2 Adding result in memoizeSet for 4 Getting value from computed result for 3 Adding result in memoizeSet for 5
n=5の場合のフィボナッチ値は次のようになります。 5
上記からわかるように、フィボナッチ数 2 と 3 は再計算されません。ここでは、計算された値を保存する HashMap を導入します。各フィボナッチ計算の前に、入力の値がコレクションで計算されているかどうかを確認します。計算されていない場合は、特定の入力の値をコレクションに追加します。
2-D の記憶
上記のプログラムには、非定数パラメーターが 1 つだけあります。次のプログラムでは、再帰呼び出しごとに値が変更される 2 つのパラメーターを持つ再帰プログラムの例を取り上げ、最適化のために 2 つの非定数パラメーターにメモ化を実装します。これは 2D メモ化と呼ばれます。
例: 標準の最長共通部分列 (LCS) を実装します。一連のシーケンスが与えられた場合、最長共通部分シーケンスの問題は、すべてのシーケンスに共通する最大長の部分シーケンスを見つけることです。可能な組み合わせは 2^n 通りあります。
例
class TP {
static int computeMax(int a, int b) {
return (a > b) ? a : b;
}
static int longestComSs(String X, String Y, int m, int n) {
if (m == 0 || n == 0)
return 0;
if (X.charAt(m - 1) == Y.charAt(n - 1))
return 1 + longestComSs(X, Y, m - 1, n - 1);
else
return computeMax(longestComSs(X, Y, m, n - 1), longestComSs(X, Y, m - 1, n));
}
public static void main(String[] args) {
String word_1 = "AGGTAB";
String word_2 = "GXTXAYB";
System.out.print("Length of LCS is " + longestComSs(word_1, word_2, word_1.length(),word_2.length()));
}
}出力
上記のコードを実行すると、次の出力が生成されます
Length of LCS is 4
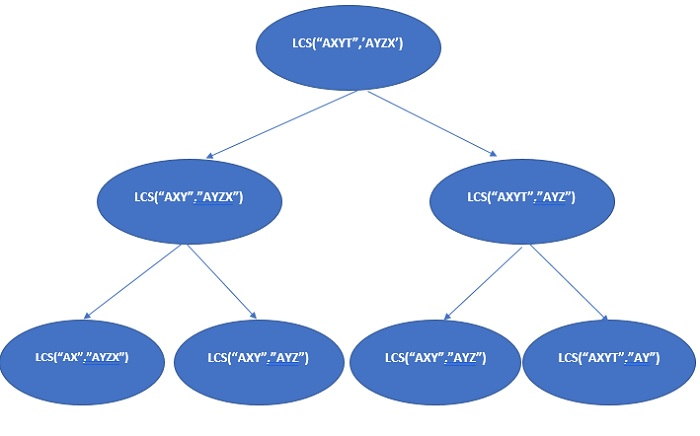
上記の再帰ツリーでは、lcs("AXY", "AYZ") が複数回解決されます。
重複する部分構造を伴うこの問題の性質により、メモ化または表作成を使用することで、同じ部分問題の繰り返し計算を回避できます。
再帰的コードのメモ化方法は次のように実装されます。
例
import java.io.*;
import java.lang.*;
class testClass {
final static int maxSize = 1000;
public static int arr[][] = new int[maxSize][maxSize];
public static int calculatelcs(String str_1, String str_2, int m, int n) {
if (m == 0 || n == 0)
return 0;
if (arr[m - 1][n - 1] != -1)
return arr[m - 1][n - 1];
if (str_1.charAt(m - 1) == str_2.charAt(n - 1)) {
arr[m - 1][n - 1] = 1 + calculatelcs(str_1, str_2, m - 1, n - 1);
return arr[m - 1][n - 1];
}
else {
int a = calculatelcs(str_1, str_2, m, n - 1);
int b = calculatelcs(str_1, str_2, m - 1, n);
int max = (a > b) ? a : b;
arr[m - 1][n - 1] = max;
return arr[m - 1][n - 1];
}
}
public static void main(String[] args) {
for (int i = 0; i < 1000; i++) {
for (int j = 0; j < 1000; j++) {
arr[i][j] = -1;
}
}
String str_1 = "AGGTAB";
String str_2 = "GXTXAYB";
System.out.println("Length of LCS is " + calculatelcs(str_1, str_2, str_1.length(),str_2.length()));
}
}出力
上記のコードを実行すると、次の出力が生成されます
Length of LCS is 4
メソッド
次のことを確認してください。 (calculatelcs) には 4 つのパラメーターがあり、そのうち 2 つは定数 (メモ化には影響しません)、および 2 つの非定数パラメーター (m および n) であり、メソッドが実行されるたびに変更されます。再帰的に呼び出される値。メモ化を実現するために、lcs(m,n) の計算値を格納する 2 次元配列を導入し、arr[m-1][n-1] に格納します。同じパラメータ m と n を使用して関数を再度呼び出すと、再帰呼び出しは実行されなくなり、以前に計算された lcs(m, n) が格納されているため、arr[m-1][n-1] が直接返されます。 arr [m-1][n-1] となり、再帰呼び出しの数が減ります。
三次元メモ化
これは、3 つの非定数パラメータを持つ再帰的プログラムのメモ化方法です。ここでは、例として 3 つの文字列の LCS 長を計算します。
ここでの方法は、指定された文字列のすべての可能なサブシーケンス (合計 3ⁿ の可能なサブシーケンスがあります) を生成し、それらの中で最も長い共通のサブシーケンスと一致することです。
計算された値を保存するための 3 次元テーブルを紹介します。サブシーケンスを考えてみましょう。
A1[1...i] i
A2[1...j] j
A3[1...k] k
共通の文字が見つかった場合 (X[i]==Y[j ]==Z[k])、残りの文字を再帰的に処理する必要があります。それ以外の場合は、
他の文字の再帰処理のために X[i] を保持する
の最大値を計算します。
他の文字の再帰処理のために Y[j] を保持する再帰処理 その他の文字
Keep Z[k] その他の文字を再帰的に処理
- したがって、上記の考え方を再帰関数に変換すると、
f(N,M,K)={1 f(N-1,M-1,K-1)if (X[N]==Y[M]==Z[K]maximum( f (N-1,M,K),f(N,M-1,K),f(N,M,K-1))}
f(N- 1 ,M,K) = 他の文字を再帰的に処理するために X[i] を予約
f(N,M-1,K) = 他の文字を再帰的に処理するために Y[j] を予約
f(N,M,K-1) = 他の文字を再帰的に処理するために Z[k] を予約します
Example
import java.io.IOException;
import java.io.InputStream;
import java.util.*;
class testClass {
public static int[][][] arr = new int[100][100][100];
static int calculatelcs(String str_1, String str_2, String str_3, int m, int n, int o) {
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
arr[i][j][0] = 0;
}
}
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= o; j++) {
arr[0][i][j] = 0;
}
}
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= o; j++) {
arr[i][0][j] = 0;
}
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= o; k++) {
if (str_1.charAt(i - 1) == str_2.charAt(j-1) && str_2.charAt(j1) == str_3.charAt(k-1)) {
arr[i][j][k] = 1 + arr[i - 1][j - 1][k - 1];
}
else {
arr[i][j][k] = calculateMax(arr[i - 1][j][k], arr[i][j - 1][k], arr[i][j][k - 1]);
}
}
}
}
return arr[m][n][o];
}
static int calculateMax(int a, int b, int c) {
if (a > b && a > c)
return a;
if (b > c)
return b;
return c;
}
public static void main(String[] args) {
String str_1 = "clued";
String str_2 = "clueless";
String str_3 = "xcxclueing";
int m = str_1.length();
int n = str_2.length();
int o = str_3.length();
System.out.print("Length of LCS is " + calculatelcs(str_1, str_2, str_3, m, n, o));
}
}Length of LCS is 4
以上がJava でのメモ化 (1D、2D、および 3D) 動的プログラミングの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7469
7469
 15
15
 1376
1376
 52
52
 77
77
 11
11
 19
19
 29
29
 Java の乱数ジェネレーター
Aug 30, 2024 pm 04:27 PM
Java の乱数ジェネレーター
Aug 30, 2024 pm 04:27 PM
Java の乱数ジェネレーターのガイド。ここでは、Java の関数について例を挙げて説明し、2 つの異なるジェネレーターについて例を挙げて説明します。
 ジャワのウェカ
Aug 30, 2024 pm 04:28 PM
ジャワのウェカ
Aug 30, 2024 pm 04:28 PM
Java の Weka へのガイド。ここでは、weka java の概要、使い方、プラットフォームの種類、利点について例を交えて説明します。
 Java Springのインタビューの質問
Aug 30, 2024 pm 04:29 PM
Java Springのインタビューの質問
Aug 30, 2024 pm 04:29 PM
この記事では、Java Spring の面接で最もよく聞かれる質問とその詳細な回答をまとめました。面接を突破できるように。
 Java 8 Stream Foreachから休憩または戻ってきますか?
Feb 07, 2025 pm 12:09 PM
Java 8 Stream Foreachから休憩または戻ってきますか?
Feb 07, 2025 pm 12:09 PM
Java 8は、Stream APIを導入し、データ収集を処理する強力で表現力のある方法を提供します。ただし、ストリームを使用する際の一般的な質問は次のとおりです。 従来のループにより、早期の中断やリターンが可能になりますが、StreamのForeachメソッドはこの方法を直接サポートしていません。この記事では、理由を説明し、ストリーム処理システムに早期終了を実装するための代替方法を調査します。 さらに読み取り:JavaストリームAPIの改善 ストリームを理解してください Foreachメソッドは、ストリーム内の各要素で1つの操作を実行する端末操作です。その設計意図はです
 Java での日付までのタイムスタンプ
Aug 30, 2024 pm 04:28 PM
Java での日付までのタイムスタンプ
Aug 30, 2024 pm 04:28 PM
Java での日付までのタイムスタンプに関するガイド。ここでは、Java でタイムスタンプを日付に変換する方法とその概要について、例とともに説明します。







