C プログラムで、以下を中国語に翻訳します: 3D の 2 つの平面間の角度
ここでは、3 次元空間の 2 つの平面間の角度を計算する方法を見ていきます。飛行機は P1 と P2 です。円周率の方程式は次のとおりです-
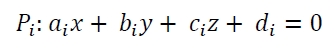
角度が「A」の場合、この規則に従います-
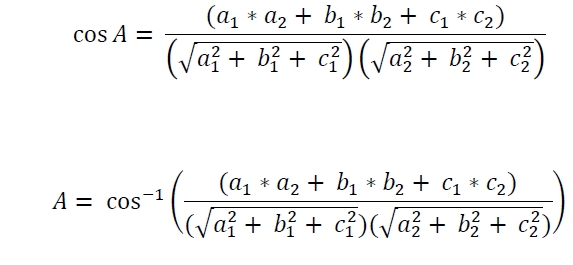
例
#include <iostream>
#include <cmath>
using namespace std;
class Plane{
private:
double a, b, c, d;
public:
Plane(double a = 0, double b = 0, double c = 0, double d = 0){
this->a = a;
this->b = b;
this->c = c;
this->d = d;
}
double friend angle(Plane p1, Plane p2);
};
double angle(Plane p1, Plane p2){
double nume = (p1.a * p2.a) + (p1.b * p2.b) + (p1.c * p2.c);
double deno1 = (p1.a * p1.a) + (p1.b * p1.b) + (p1.c * p1.c);
double deno2 = (p2.a * p2.a) + (p2.b * p2.b) + (p2.c * p2.c);
return (180.0 / 3.14159) * acos(nume/ (sqrt(deno1) * sqrt(deno2)));
}
int main() {
Plane p1(2.0, 2.0, -3.0, -5.0), p2(3.0, -3.0, 5.0, -6.0);
cout << "Angle: " << angle(p1, p2) << " degree";
}出力
Angle: 123.697 degree
以上がC プログラムで、以下を中国語に翻訳します: 3D の 2 つの平面間の角度の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7476
7476
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 31
31
 Python で 3D 地理グラフを描画する方法
Sep 28, 2023 am 10:19 AM
Python で 3D 地理グラフを描画する方法
Sep 28, 2023 am 10:19 AM
Python で 3D 地理グラフを描画する方法の概要: 3D 地理グラフを描画すると、地理データと空間分布をより直観的に理解するのに役立ちます。 Python は強力で使いやすいプログラミング言語として、さまざまな種類の地理図を描画するためのライブラリとツールを多数提供しています。この記事では、Python プログラミング言語と、Matplotlib や Basemap などのいくつかの人気のあるライブラリを使用して 3D 地理グラフを描画する方法を学びます。環境の準備: 開始する前に、次のことを確認する必要があります。
 Vue を使用して 3D 立体回転効果を実現する方法
Sep 19, 2023 am 08:42 AM
Vue を使用して 3D 立体回転効果を実現する方法
Sep 19, 2023 am 08:42 AM
Vue を使用して 3D 3 次元回転効果を実現する方法 人気のあるフロントエンド フレームワークとして、Vue.js は動的な Web ページやアプリケーションの開発において重要な役割を果たします。インタラクティブなインターフェイスを構築する直感的かつ効率的な方法を提供し、統合と拡張が簡単です。この記事では、Vue.js を使用して見事な 3D 立体回転効果を実装する方法を紹介し、具体的なコード例を示します。始める前に、Vue.js がインストールされていること、および Vue.js の基本的な使用法をある程度理解していることを確認してください。まだなら
 Vue と Canvas を使用してクールな 3D 回転グラフィックスを作成する方法
Jul 17, 2023 pm 03:42 PM
Vue と Canvas を使用してクールな 3D 回転グラフィックスを作成する方法
Jul 17, 2023 pm 03:42 PM
Vue と Canvas を使用してクールな 3D 回転グラフィックスを作成する方法 はじめに: Vue と Canvas は 2 つの非常に強力なフロントエンド テクノロジであり、それぞれページ レンダリングと画像描画の処理に優れています。この記事では、Vue と Canvas を組み合わせてクールな 3D 回転グラフィックス効果を作成する方法を紹介します。 Vue を使用して基本的なページ構造を構築する方法と、Canvas を使用して 3D グラフィックスの描画および回転効果を実現する方法を説明します。この記事を読むことで、VueとCanvasの活用方法が理解できるようになります。
 Vue を使用して 3D 反転効果を実装する方法
Sep 21, 2023 pm 02:04 PM
Vue を使用して 3D 反転効果を実装する方法
Sep 21, 2023 pm 02:04 PM
Vue を使用して 3D 反転効果を実装する方法 はじめに: Vue.js は、高度にインタラクティブな Web アプリケーションの構築に役立つ人気のある JavaScript フレームワークです。この記事では、Vue.js を使用してクールな 3D 反転効果を実装する方法を検討し、参照用の具体的なコード例を示します。はじめに: 3D フリップ効果は、Web サイトやアプリケーションにインタラクティブ性と魅力を追加できます。 Vue.js は、柔軟で使いやすいフロントエンド フレームワークとして、これを簡単に実現できます。
 3D チャートを使用してハイチャートにデータを表示する方法
Dec 18, 2023 am 08:18 AM
3D チャートを使用してハイチャートにデータを表示する方法
Dec 18, 2023 am 08:18 AM
Highcharts は、3D グラフを含むさまざまな種類のグラフを提供する、非常に人気のある JavaScript グラフ作成ライブラリです。この記事では、3D チャートを使用してハイチャートにデータを表示する方法を詳しく紹介し、具体的なコード例を示します。 Highcharts ライブラリの導入 まず、HTML ファイルに Highcharts ライブラリを導入する必要があります。これは次の方法で実現できます: <scriptsrc="https://
 メタバース リモート会議における 2D と 3D 間のシームレスな移行を実現する Microsoft の特許共有
Dec 27, 2023 am 10:54 AM
メタバース リモート会議における 2D と 3D 間のシームレスな移行を実現する Microsoft の特許共有
Dec 27, 2023 am 10:54 AM
(Nweon 2023年12月26日) 遠隔会議の発展によりメタバースの普及が進んでいる。ただし、現在のオンライン会議アプリケーションは、メタ環境を使用するときに、すべての参加者が同じ種類のデバイスを使用しているわけではないという大きな問題に直面しています。たとえば、PC から操作するユーザーもいれば、VR ヘッドセットを使用するユーザーもいますが、デスクトップ ユーザーは、仮想環境内のすべてのユーザーを操作したり対話したりできないため、不利な立場に置かれることがあります。コンピュータは 3D 環境の 2D ビューを提供しますが、コンピュータが 3D 環境をナビゲートしたり操作したりするためにユーザーから入力ジェスチャを受け取る方法には制限があります。現在の観点から見ると、テクノロジーは急速に発展していますが、VR ヘッドセット ユーザーと PC ユーザーの体験は同じではありません。また、からかどうか
 CSS 3D 変換プロパティ: 変換と遠近法
Oct 26, 2023 am 08:54 AM
CSS 3D 変換プロパティ: 変換と遠近法
Oct 26, 2023 am 08:54 AM
CSS3D 変換プロパティ: 変換とパースペクティブ、特定のコード サンプルが必要 CSS3D 変換プロパティは、いくつかの単純なコードで素晴らしい視覚効果を実現できる強力なテクニックです。それらの中で、最も一般的に使用される 2 つの属性は、transform と Perspective です。 1. Transform 属性 Transform 属性は、要素の回転、拡大縮小、傾き、移動などの操作を実行するために使用されます。そうでない場合でも設定できます
 Golang フレームワークと D 言語フレームワーク: 高性能プログラミングへの同様のアプローチ
Jun 06, 2024 pm 01:09 PM
Golang フレームワークと D 言語フレームワーク: 高性能プログラミングへの同様のアプローチ
Jun 06, 2024 pm 01:09 PM
Go フレームワークと D フレームワークはどちらも、シンプルさ、拡張性、使いやすさを備えた高パフォーマンスの Web アプリケーションを構築するために使用できます。 Go フレームワーク: Echo (軽量 Web フレームワーク)、Gin (REST API および複雑な Web アプリケーション)、Gorilla (共通タスク ツールキット) D フレームワーク: Tango (高性能 Web アプリケーション開発)、Dodo (フルスタック Web フレームワーク)、Viper ( ORM フレームワーク) パフォーマンス: Go フレームワークと D フレームワークは同様のパフォーマンスを持ち、区別するのは困難です。 同時実行性: Go コルーチンは軽量の並列処理を提供し、D 純粋スレッド モデルは細かい制御を提供します。 構文: Go 構文はシンプルで、D 構文は複雑で機能が豊富です。特定のアプリケーション要件と開発によって異なります




