行列が非対称かどうかをチェックするCプログラム?

すべての i と j について、正方行列 A の要素が aij=−aji を満たす場合、正方行列 A は非対称行列と呼ばれます。言い換えれば、行列 A の転置が行列 A の負の値に等しい場合、つまり (AT=-A) の場合、行列 A は非対称行列と呼ばれます。
非対称行列の主対角要素はすべて 0 であることに注意してください。
行列の例を見てみましょう
A= |0 -5 4| |5 0 -1| |-4 1 0|
すべての i と j について、aij=−aji であるため、これは歪対称行列です。たとえば、a12 = -5、a21 = 5、つまり a12 = −a21 となります。同様に、この条件は i と j の他のすべての値にも当てはまります。
行列 A の転置が行列 A の負の数、つまり AT=−A に等しいことも検証できます。
A<sup>T</sup>= |0 5 -4|
|-5 0 1|
|4 -1 0|
and
A= |0 -5 4|
|5 0 -1|
|-4 1 0|AT=−A であることが明確にわかります。これにより、A は歪対称行列になります。
Input: Enter the number of rows and columns: 2 2 Enter the matrix elements: 10 20 20 10 Output: The matrix is symmetric. 10 20 20 10
説明
行列は、転置行列と等しい場合、対称行列です。
それ以外の場合、転置が負に等しい場合、行列は非対称になります。それ以外の場合は、対称でも反対称でもありません。結果はそれに応じて印刷されます。
行列の対称性をチェックするプロセスは次のとおりです。
ユーザーは行列の行数と列数を入力する必要があります。
入力行列の要素が必要で、それらを 'A' に格納します。変数「x」と「y」を 0 に初期化します。
行列が転置と等しくない場合は、一時変数 'x' に値 1 を割り当てます。
それ以外の場合、行列の負の数がその転置に等しい場合は、値 1 を一時変数 'y' に割り当てます。
x が 0 に等しい場合、行列は対称です。それ以外の場合、y が 1 に等しい場合、行列は非対称になります。
上記の条件がいずれも満たされない場合、行列は対称でも非対称でもありません。
次に、結果を出力します。
例
#include<iostream>
using namespace std;
int main () {
int A[10][10], i, j, m, n, x = 0, y = 0;
cout << "Enter the number of rows and columns : ";
cin >> m >> n;
cout << "Enter the matrix elements : ";
for (i = 0; i < m; i++)
for (j = 0; j < n; j++)
cin >> A[i][j];
for (i = 0; i < m; i++) {
for( j = 0; j < n; j++) {
if (A[i][j] != A[j][i])
x = 1;
else if (A[i][j] == -A[j][i])
y = 1;
}
}
if (x == 0)
cout << "The matrix is symmetric.</p><p> ";
else if (y == 1)
cout << "The matrix is skew symmetric.</p><p> ";
else
cout << "It is neither symmetric nor skew-symmetric.</p><p> ";
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++)
cout << A[i][j] << " ";
cout << "</p><p> ";
}
return 0;
}以上が行列が非対称かどうかをチェックするCプログラム?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7514
7514
 15
15
 1378
1378
 52
52
 79
79
 11
11
 19
19
 64
64
 以下を中国語に翻訳してください: ローマ数字を 10 進数に変換する C プログラム
Sep 05, 2023 pm 09:53 PM
以下を中国語に翻訳してください: ローマ数字を 10 進数に変換する C プログラム
Sep 05, 2023 pm 09:53 PM
以下に、ローマ数字を 10 進数に変換する C 言語アルゴリズムを示します。 アルゴリズム ステップ 1 - 開始 ステップ 2 - 実行時にローマ数字を読み取る ステップ 3 - 長さ: = strlen(roman) ステップ 4 - i=0 から長さ-1 の場合 ステップ4.1-switch(roman[i]) ステップ 4.1.1-case'm': &nbs
 人工知能の歴史とマトリックスを探る: 人工知能チュートリアル (2)
Nov 20, 2023 pm 05:25 PM
人工知能の歴史とマトリックスを探る: 人工知能チュートリアル (2)
Nov 20, 2023 pm 05:25 PM
このシリーズの最初の記事では、人工知能、機械学習、深層学習、データ サイエンスなどのつながりと違いについて説明しました。また、シリーズ全体で使用するプログラミング言語やツールなどについても、いくつかの難しい選択をしました。最後に、行列の知識も少し紹介しました。この記事では、人工知能の中核であるマトリックスについて詳しく説明します。その前に、まず人工知能の歴史を理解しましょう。なぜ人工知能の歴史を理解する必要があるのでしょうか?歴史上何度もAIブームはありましたが、多くの場合、AIの可能性に対する大きな期待は実現しませんでした。人工知能の歴史を理解すると、この人工知能の波が奇跡を起こすのか、それともはじけようとしている単なるバブルなのかを知ることができます。私たち
 指定された値を引数として受け取る逆双曲線正弦関数の値を見つける C++ プログラム
Sep 17, 2023 am 10:49 AM
指定された値を引数として受け取る逆双曲線正弦関数の値を見つける C++ プログラム
Sep 17, 2023 am 10:49 AM
双曲線関数は、円の代わりに双曲線を使用して定義され、通常の三角関数と同等です。ラジアン単位で指定された角度から双曲線正弦関数の比率パラメーターを返します。しかし、その逆、つまり別の言い方をすればいいのです。双曲線正弦から角度を計算したい場合は、双曲線逆正弦演算のような逆双曲線三角関数演算が必要です。このコースでは、C++ で双曲線逆サイン (asinh) 関数を使用し、ラジアン単位の双曲線サイン値を使用して角度を計算する方法を説明します。双曲線逆正弦演算は次の式に従います -$$\mathrm{sinh^{-1}x\:=\:In(x\:+\:\sqrt{x^2\:+\:1})}ここで\:In\:is\:自然対数\:(log_e\:k)
 リンクリストの長さを求めるCプログラム
Sep 07, 2023 pm 07:33 PM
リンクリストの長さを求めるCプログラム
Sep 07, 2023 pm 07:33 PM
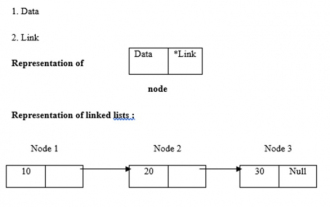
リンク リストは動的なメモリ割り当てを使用します。つまり、リンク リストはそれに応じて拡大および縮小します。これらはノードのコレクションとして定義されます。ここで、ノードにはデータとリンクという 2 つの部分があります。データ、リンク、リンクリストの表現は以下のとおりです。 ・リンクリストの種類 リンクリストには以下の4種類があります。 ・シングルリンクリスト/シングルリンクリスト ダブル/ダブルリンクリスト 循環シングルリンクリスト 循環ダブルリンクリスト再帰的メソッドを使用してリンク リストの長さを確認します。ロジックは -intlength(node *temp){ if(temp==NULL) returnl; else{&n
 C プログラムは rename() 関数を使用してファイル名を変更します
Sep 21, 2023 pm 10:01 PM
C プログラムは rename() 関数を使用してファイル名を変更します
Sep 21, 2023 pm 10:01 PM
名前変更機能は、ファイルまたはディレクトリを古い名前から新しい名前に変更します。この操作は移動操作と似ています。したがって、この名前変更機能を使用してファイルを移動することもできます。この関数は、stdio.h ライブラリ ヘッダー ファイルに存在します。 rename 関数の構文は次のとおりです: intrename(constchar*oldname,constchar*newname); rename() 関数は 2 つのパラメータを受け取ります。 1 つは古い名前、もう 1 つは新しい名前です。どちらのパラメータも、ファイルの古い名前と新しい名前を定義する定数文字へのポインタです。ファイルの名前が正常に変更された場合はゼロを返し、それ以外の場合はゼロ以外の整数を返します。名前変更操作中
 辞書を印刷する C++ プログラム
Sep 11, 2023 am 10:33 AM
辞書を印刷する C++ プログラム
Sep 11, 2023 am 10:33 AM
マップは C++ の特別なタイプのコンテナで、各要素は 2 つの値、つまりキー値とマップ値のペアです。キー値は各項目のインデックス付けに使用され、マップされた値はキーに関連付けられた値です。マップされた値が一意であるかどうかに関係なく、キーは常に一意です。 C++ でマップ要素を出力するには、反復子を使用する必要があります。項目のセット内の要素は、反復子オブジェクトによって示されます。イテレータは主に配列や他のタイプのコンテナ (ベクトルなど) で使用され、特定の範囲内の特定の要素を識別するために使用できる特定の操作セットを備えています。イテレータをインクリメントまたはデクリメントして、範囲またはコンテナ内に存在するさまざまな要素を参照できます。イテレータは、範囲内の特定の要素のメモリ位置を指します。イテレータを使用して C++ でマップを出力する まず、定義方法を見てみましょう。
 多次元配列を使用して 2 つの行列を乗算する Python プログラム
Sep 11, 2023 pm 05:09 PM
多次元配列を使用して 2 つの行列を乗算する Python プログラム
Sep 11, 2023 pm 05:09 PM
行列は、行と列に配置された一連の数値です。 m 行 n 列の行列は mXn 行列と呼ばれ、m と n はその次元と呼ばれます。行列は、リストまたは NumPy 配列を使用して Python で作成された 2 次元配列です。一般に、行列の乗算は、最初の行列の行と 2 番目の行列の列を乗算することで実行できます。ここで、最初の行列の列数は 2 番目の行列の行数と等しくなければなりません。入力シナリオと出力シナリオ 2 つの行列 A と B があるとします。これら 2 つの行列の次元は、それぞれ 2X3 と 3X2 です。乗算後の結果の行列は 2 行 1 列になります。 [b1,b2][a1,a2,a3]*[b3,b4]=[a1*b1+a2*b2+a3*a3][a4,a5,a6][b5,b6][a4*b2+a
 strncmp ライブラリ関数を使用して 2 つの文字列を比較する C プログラムを作成します。
Sep 09, 2023 pm 01:17 PM
strncmp ライブラリ関数を使用して 2 つの文字列を比較する C プログラムを作成します。
Sep 09, 2023 pm 01:17 PM
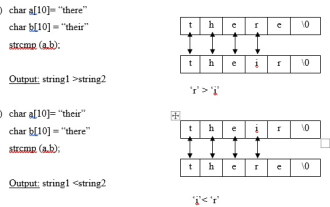
Strncmp は、string.h ファイル内に存在する定義済みライブラリ関数で、2 つの文字列を比較し、どちらの文字列が大きいかを表示するために使用されます。 strcmp 関数 (文字列比較) この関数は 2 つの文字列を比較します。 2 つの文字列内の最初の不一致文字の ASCII 差異を返します。構文 intstrcmp(string1,string2); 差がゼロに等しい場合は、string1=string2 となります。差が正の場合、文字列 1 > 文字列 2 になります。差が負の場合は、string1<string2 となります。 strncmp 関数の例 この関数は、2 つの文字列の最初の n 文字を比較するために使用されます。構文 strn




