ツリー内の最短パスのすべてのペアの合計

ツリーでは、「ノードのすべてのペアの最短パスの合計」という用語は、ノードのすべてのペアの個々の最短パスの合計の計算を指します。効果的な方法は、デュアル DFS (深さ優先検索) アルゴリズムを使用することです。選択したノードと他のすべてのノードの間の距離は、最初の DFS パス中に決定されます。ツリーは 2 回目の DFS パス中に再び走査され、各ノードを潜在的な LCA (最下位共通祖先) とみなして、選択された LCA の子孫ノードのペア間の距離の合計を計算します。この方法を使用すると、ツリー内のノードのすべてのペアの最短パスの合計を計算し、理想的なソリューションを保証できます。
使用説明書
Double DFS (深さ優先探索) 方式
動的プログラミング手法
Double DFS (深さ優先探索) 方式
ツリー内の最短パスのすべてのペアの合計には、2 つの DFS パスを含むデュアル DFS (深さ優先検索) メソッドを使用します。まず、任意のノードから他のすべてのノードまでの距離を計算します。次に、2 回目の DFS トラバーサル中に、各ノードを潜在的な LCA として考慮しながらツリー内を移動します。トラバース中に、選択した LCA の子孫であるノードのペア間の距離を計算して合計します。すべてのノードに対してこのプロセスを繰り返すことにより、最短パスのすべてのペアの合計が得られます。この戦略は、ツリー内のすべてのノード セット間の距離の合計を効率的に計算できるため、この問題に対して非常に説得力があります。
###アルゴリズム###- ツリー内の任意のノードを開始ノードとして使用できます
-
Example
リーリー ###出力### リーリー動的プログラミング手法:
最初に任意のノードをルート ノードとして選択し、動的計画法でツリーをルート付きツリーに変換します。これは、ツリー内のすべてのノード間の最短パスの合計を計算するために使用されます。動的プログラミングを使用して、各ノードとルート ノード間の分割を計算し、結果を配列に保存します。次に、各ノードについて、ルート ノードからの子の (計算された) 距離を追加して、他のすべてのノードの全体的な距離を決定します。このようにして、すべてのノード間の最短パスの総数をすばやく計算できます。この問題を解決する効率的な方法として、このアルゴリズムの時間計算量は O(N) です。ここで、N はツリー内のノードの数です。
###アルゴリズム### ツリー内の任意のノードをルートとして取得し、(たとえば、ルート ノードの深さ検索を使用して) ツリーをルート化して、ルート化されたツリーを作成します。
- 動的プログラミングを使用して、ルートから各ノードの距離を決定できます。これらの距離は、配列またはデータ構造に格納する必要があります。
- a. 現在のノードの子ノードを走査します。
b. 現在のノードを通るパスを検討するには、各サブツリーのサブツリー内のノードの数と、各サブツリーについて以前に計算されたルートまでの距離を加算します。
c. アクティブ ノードの子ノードごとに、次の金額を追加します。
-
リーリー
###出力###
リーリー
###結論は###
ツリー内の最短パスのすべてのペアの合計は、Double DFS (深さ優先検索) メソッドまたは動的プログラミングを使用して計算できます。 Double DFS メソッドは 2 つのパスで構成されます。最初に選択したノードから他のすべてのノードまでの距離を計算し、次に各ノードを潜在的な最低共通祖先 (LCA) として扱いながらツリーを再度走査して、子孫ノードのペア間の距離を合計します。動的プログラミング手法では、DFS を再帰的に使用してツリーのルートを構築し、ルートから他のすべてのノードまでの距離を計算する必要があります。どちらの方法の結果も同じで、ツリー内のすべてのペアごとの最短パスの合計で構成されます。 2 つのアルゴリズムのどちらを選択するかは、特定の実装設定またはツリー構造に基づいて決定される可能性がありますが、どちらのアルゴリズムも効率的なソリューションを提供します。
d. 現在のノードの合計を最終結果に追加します。
ツリー内の最短パスのすべてのペアの合計が最終結果になります。
以上がツリー内の最短パスのすべてのペアの合計の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7513
7513
 15
15
 1378
1378
 52
52
 79
79
 11
11
 19
19
 64
64
 ツリー内の最短パスのすべてのペアの合計
Aug 28, 2023 pm 03:17 PM
ツリー内の最短パスのすべてのペアの合計
Aug 28, 2023 pm 03:17 PM
ツリーでは、「ノードのすべてのペアの最短パスの合計」という用語は、ノードのすべてのペアの個々の最短パスの合計の計算を指します。効果的な方法は、デュアル DFS (深さ優先検索) アルゴリズムを使用することです。選択したノードと他のすべてのノードの間の距離は、最初の DFS パス中に決定されます。ツリーは 2 回目の DFS パス中に再び走査され、各ノードを潜在的な LCA (最下位共通祖先) とみなして、選択された LCA の子孫ノードのペア間の距離の合計を計算します。この方法を使用すると、ツリー内のノードのすべてのペアの最短パスの合計を計算し、理想的な解を確実に得ることができます。 使用される方法 デュアル DFS (深さ優先検索) メソッド ダイナミック プログラミング メソッド ツリーのデュアル DFS (深さ優先検索) メソッド すべて最短経路のペア
 Javaを使用して最短パスアルゴリズムを実装する方法
Sep 19, 2023 am 08:18 AM
Javaを使用して最短パスアルゴリズムを実装する方法
Sep 19, 2023 am 08:18 AM
Java を使用して最短パス アルゴリズムを実装する方法の概要: 最短パス アルゴリズムはグラフ理論の重要なアプリケーションであり、ネットワーク ルーティング、マップ ナビゲーション、その他の分野で広く使用されています。この記事では、Java を使用して最短パス アルゴリズムを実装する方法を学び、具体的なコード例を示します。アルゴリズムのアイデア: 最短経路アルゴリズムを実装するには多くの方法がありますが、その中で最も有名な 2 つのアルゴリズムは、ダイクストラ アルゴリズムと A* アルゴリズムです。ここでは、ダイクストラのアルゴリズムの実装に焦点を当てます。ダイクストラのアルゴリズムの基礎
 Java におけるツリーとグラフの非線形データ構造のアプリケーションと実装方法の詳細な調査
Dec 26, 2023 am 10:22 AM
Java におけるツリーとグラフの非線形データ構造のアプリケーションと実装方法の詳細な調査
Dec 26, 2023 am 10:22 AM
Java のツリーとグラフの理解: 非線形データ構造のアプリケーションと実装の探索 はじめに コンピューター サイエンスでは、データ構造はコンピューター内でデータを保存、編成、管理する方法です。データ構造は、線形データ構造と非線形データ構造に分類できます。ツリーとグラフは、最も一般的に使用される 2 つのタイプの非線形データ構造です。この記事では、Java におけるツリーとグラフの概念、アプリケーション、実装に焦点を当て、具体的なコード例を示します。ツリーの概念と応用 ツリーは抽象データ型であり、ノードとエッジの集合です。ツリーの各ノードには番号が含まれています
 C++ データ構造における再帰の素晴らしい使用法: スタックとツリーの実装
May 04, 2024 pm 01:54 PM
C++ データ構造における再帰の素晴らしい使用法: スタックとツリーの実装
May 04, 2024 pm 01:54 PM
C++ データ構造における再帰の適用: スタック: スタックは、後入れ先出し (LIFO) 構造を通じて再帰的に実装されます。ツリー: ツリーは階層構造を通じて再帰的に実装され、挿入や深さの計算などの操作をサポートします。再帰は、ネストされた構造を処理するための簡潔で効率的なソリューションを提供し、データ構造の実装をより直感的で保守しやすくします。
 Floyd-Warshal アルゴリズムを使用して、任意の 2 つのノード間の最短パスを検索します。
Sep 20, 2023 pm 02:21 PM
Floyd-Warshal アルゴリズムを使用して、任意の 2 つのノード間の最短パスを検索します。
Sep 20, 2023 pm 02:21 PM
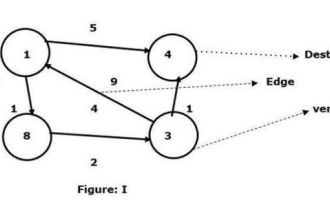
C++ にはコードの一部または期待値として定義されるマクロがあり、ユーザーが必要とするたびに再利用されます。フロイド・ウォルシャル アルゴリズムは、指定された重み付きグラフ内の頂点のすべてのペア間の最短経路を見つけるプロセスです。このアルゴリズムは動的プログラミング アプローチに従って、最小重みグラフを見つけます。図を通してフロイド・ウォルシャルアルゴリズムの意味を理解しましょう - 頂点 1 をソースとして、頂点 4 を目的地として取り、それらの間の最短パスを見つけます。ターゲット頂点 4 に接続できるパスが 2 つあることがわかりました。 1->4 – エッジの重みは 51->8->3->4 – エッジの重み (1+2+1)は4です。与えられたグラフ I では、2 つの頂点を接続する最小のエッジが表示されます。ここに頂点があります
 PHP アルゴリズム設計のアイデア: グラフの最短経路問題に対する効率的な解決策を達成するには?
Sep 19, 2023 pm 03:43 PM
PHP アルゴリズム設計のアイデア: グラフの最短経路問題に対する効率的な解決策を達成するには?
Sep 19, 2023 pm 03:43 PM
PHP アルゴリズム設計のアイデア: グラフの最短経路問題に対する効率的な解決策を達成するには?実際の開発では、地図ナビゲーション、ネットワークルーティング、物流流通などの分野で、最短経路の問題を解決する必要があることがよくあります。この種の問題を解決するには、グラフの最短パス アルゴリズムが鍵となります。グラフは、頂点のセットとエッジのセットで構成されます。頂点はノードを表し、エッジはノード間の関係を表します。最短パスの問題は、2 つのノードを接続する最短パスを見つけることです。 PHP では、さまざまなアルゴリズムを使用して最短経路問題を解決できます。その中で最も有名なものは次のとおりです。
 C++ を使用して、どのパス上にも存在せず、パスの合計が k 未満であるすべてのノードを削除します。
Sep 04, 2023 am 10:17 AM
C++ を使用して、どのパス上にも存在せず、パスの合計が k 未満であるすべてのノードを削除します。
Sep 04, 2023 am 10:17 AM
この問題では、ルート ノードからリーフ ノードまでのパスが完全に定義されたバイナリ ツリーがあります。ルート ノードからリーフ ノードまでのすべてのノードの合計は k 以上である必要があります。したがって、合計が k 未満であるパス内のすべてのノードを削除する必要があります。ここで覚えておくべき重要なことは、ノードは多くのパスの一部である可能性があるため、残っているすべてのパスの合計が 10+20+5 (つまり 25、つまり 150 未満) の場合にのみ、ノードをプルーニングして削除する必要があるということです。 5.その後、10→30→40と評価してみましょう。 150未満なので40を削除します。ここで、別のパス 10->20->35->50 が表示され、合計 115 は 150 未満になります。
 パスを満たさず、k 以上のノードを削除する C++ プログラム
Sep 14, 2023 am 11:25 AM
パスを満たさず、k 以上のノードを削除する C++ プログラム
Sep 14, 2023 am 11:25 AM
この問題では、ルート ノードからリーフ ノードまでのパスが完全に定義されたバイナリ ツリーがあります。ルート ノードからリーフ ノードまでのすべてのノードの合計は、定数値 k 以上である必要があります。したがって、ツリー内の残りのパスが k より大きくなるように、パス内の合計が k より小さいノードをすべて削除する必要があります。ここで覚えておくべき重要なことは、ノードは多くのパスの一部である可能性があるため、そのノードに至るすべてのパスの合計 (左) が 10+20+5 (つまり 25 で 150 未満) になる場合にのみ、 5をトリミングして削除します。その後、10→30→40と評価してみましょう。 150未満なので40を削除します。ここで、別のパス 10->20- が表示されます。




