指定されたバイナリ ツリー内で最大のバイナリ検索サブツリーを見つける - C++ のエピソード 1

この問題では、二分木 BT が与えられます。私たちのタスクは、指定された二分木で 最大の二分検索サブツリーを見つけることです。

バイナリ ツリーは、データの保存に使用される特別なデータ構造です。バイナリ ツリーには、各ノードが最大 2 つの子ノードを持つことができるという特別な条件があります。

二分探索木 (BST) は、次の特性を満たす木です。

• 左のサブツリーのキー値が親ノードのキー値より小さい(ルートノード) の値。

• 右サブツリーのキー値は、その親ノード (ルート ノード) のキー値以上です。

この問題を理解するために例を挙げてみましょう。

次のように入力してください:

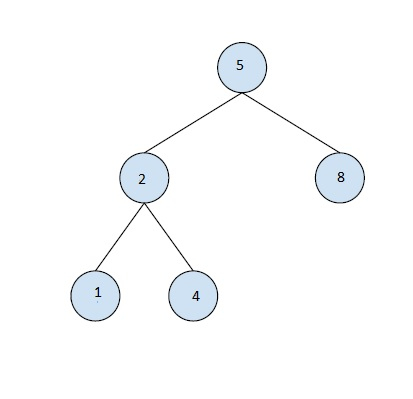
出力: 3

説明

Full binary tree is a BST.

解決策

問題を解決する簡単な方法は、ツリーを順番に走査することです。ツリーの各ノードについて、そのサブツリーが二分探索ツリーであるかどうかを確認します。最後に、最大の二分探索サブツリーのサイズが返されます。

例

ソリューションがどのように機能するかを示す手順の例

#include<bits/stdc++.h>
using namespace std;
class node{
   public:
   int data;
   node* left;
   node* right;
   node(int data){
      this->data = data;
      this->left = NULL;
      this->right = NULL;
   }
};
int findTreeSize(node* node) {
   if (node == NULL)
      return 0;
   else
      return(findTreeSize(node->left) + findTreeSize(node->right) + 1);
}
int isBSTree(struct node* node) {
   if (node == NULL)
      return 1;
   if (node->left != NULL && node->left->data > node->data)
      return 0;
   if (node->right != NULL && node->right->data < node->data)
      return 0;
   if (!isBSTree(node->left) || !isBSTree(node->right))
      return 0;
   return 1;
}
int findlargestBSTSize(struct node *root) {
   if (isBSTree(root)){
      return findTreeSize(root);
}
else
   return max(findlargestBSTSize(root->left), findlargestBSTSize(root->right));
}
int main() {
   node *root = new node(5);
   root->left = new node(2);
   root->right = new node(8);
   root->left->left = new node(1);
   root->left->right = new node(4);
   cout<<"The size of the largest possible BST is "<<findlargestBSTSize(root);
   return 0;
}

出力

The size of the largest possible BST is 5

別のアプローチ

別のアプローチこの問題を解決する方法は、ツリーを下からたどって、その子ノードによって BST であるかどうかを確認することです。これを行うために、

が BST であるかどうかを追跡します。

• 左側のサブツリーの場合、最大の要素の値。

• 右側のサブツリーの場合、最小要素の値。 BST を確認するには、これらの値を現在のノードと比較する必要があります。

さらに、最大 BST のサイズは、現在の BST のサイズと比較することによって更新されます。

例

#include<bits/stdc++.h>
using namespace std;
class node{
   public:
   int data;
   node* left;
   node* right;
   node(int data){
      this->data = data;
      this->left = NULL;
      this->right = NULL;
   }
};
int findlargestBSTSizeRec(node* node, int *minValRsubTree, int *maxValLsubTree, int *maxBSTSize, bool *isBSTree) {
   if (node == NULL){
      *isBSTree = true;
      return 0;
   }
   int min = INT_MAX;
   bool left_flag = false;
   bool right_flag = false;
   int leftSubtreeSize,rightSubTreeSize;
   *maxValLsubTree = INT_MIN;
   leftSubtreeSize = findlargestBSTSizeRec(node->left, minValRsubTree, maxValLsubTree, maxBSTSize, isBSTree);
   if (*isBSTree == true && node->data > *maxValLsubTree)
      left_flag = true;
   min = *minValRsubTree;
   *minValRsubTree = INT_MAX;
   rightSubTreeSize = findlargestBSTSizeRec(node->right, minValRsubTree, maxValLsubTree, maxBSTSize, isBSTree);
   if (*isBSTree == true && node->data < *minValRsubTree)
      right_flag = true;
   if (min < *minValRsubTree)
      *minValRsubTree = min;
   if (node->data < *minValRsubTree)
      *minValRsubTree = node->data;
   if (node->data > *maxValLsubTree)
      *maxValLsubTree = node->data;
   if(left_flag && right_flag){
      if (leftSubtreeSize + rightSubTreeSize + 1 > *maxBSTSize)
         *maxBSTSize = (leftSubtreeSize + rightSubTreeSize + 1);
      return (leftSubtreeSize + rightSubTreeSize + 1);
   }
   else{
      *isBSTree = false;
      return 0;
   }
}
int findlargestBSTSize(node* node){
   int min = INT_MAX;
   int max = INT_MIN;
   int largestBSTSize = 0;
   bool isBST = false;
   findlargestBSTSizeRec(node, &min, &max, &largestBSTSize, &isBST);
   return largestBSTSize;
}
int main(){
   node *root = new node(5);
   root->left = new node(2);
   root->right = new node(8);
   root->left->left = new node(1);
   root->left->right = new node(4);
   cout<<"The Size of the largest BST is "<<findlargestBSTSize(root);
   return 0;
}

出力

The Size of the largest BST is 5

以上が指定されたバイナリ ツリー内で最大のバイナリ検索サブツリーを見つける - C++ のエピソード 1の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。