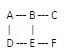指定された条件に基づいて配列から構築されたグラフにサイクルが含まれているかどうかを確認します-＆＃＆チュートリアル-php.cn

指定された条件に基づいて配列から構築されたグラフにサイクルが含まれているかどうかを確認します

WBOY

リリース： 2023-08-31 18:57:06

転載

790 人が閲覧しました

＃＃＃＃＃＃導入＃＃＃

グラフ理論では、配列から構成され、特定の条件を満たすグラフに周期があるかどうかを解明することが非常に重要な作業です。図は、物事がどのように接続されているかを示す想像力豊かな方法です。コンピュータネットワークやソーシャルネットワークなど、さまざまな場所で使用されています。この記事では、グラフ構築の条件、BFS および DFS アルゴリズムについて説明し、無向グラフのサイクルを識別する方法について段階的に説明します。

グラフの配列表現

グラフ理論の配列ベースのメソッドは頂点とエッジを配列に保存するため、アルゴリズムでの使用と操作が容易になります。空のグラフから始めて、配列内の情報に基づいて頂点とエッジを 1 つずつ追加することは、サイクル検出などのさらなる探索の基礎となります。これは、グラフがどのようにリンクされているか、およびサイクルがあるかどうかを理解するために重要です。

グラフ構築条件

与えられた条件の説明

グラフは配列から構築されます。配列は頂点のセットとその接続またはエッジを表します。

配列の各要素はグラフの頂点に対応します
配列内の各要素の値は、接続されている頂点 (隣接する頂点) のインデックスを表します。
配列のインデックスは頂点自体を表し、それに対応する値は接続されている頂点を表します。
グラフ構築を検証するための条件

チャートを作成する前に、配列が有効であり、必要な条件を満たしていることを確認してください。

配列が空ではなく、頂点を作成するための要素が少なくとも 1 つ含まれていることを確認してください。
負の値または無効なデータは有効な頂点またはエッジを表すことができないため、配列に負ではない整数のみが含まれていることを確認してください。
配列インデックスが適切な範囲内にあることを確認してください。それらは 0 から始まり、n-1 まで進む必要があります。ここで、n はグラフ内の頂点の総数です。
配列内の値 (接続) も 0 から n-1 の有効な範囲内にあることを確認し、それらが既存の頂点に対応していることを確認します
有効なグラフの条件に違反する重複した接続または自己ループがあるかどうかを確認してください
接続が失われていないこと、つまりすべての頂点が接続されて完全なグラフまたは接続されたコンポーネントが形成されていることを確認します
DFS および BFS アルゴリズム

深さ優先検索 (DFS) は、方向転換する前に各ブランチをできるだけ深く掘り下げてグラフの頂点とエッジを探索するために使用されます。

疑似コード
リーリー

幅優先検索 (BFS) は、グラフのすべての頂点を一度に 1 層ずつ走査するグラフ走査アルゴリズムです。これは、チャートでサイクルを見つける良い方法になります

疑似コード
リーリー＃＃＃複雑＃＃＃

時間計算量

BFS と DFS の時間計算量は両方とも O(V E) です。ここで、V は頂点の数、E はエッジの数です。

空間の複雑さ

ステップバイステップのサイクル検出プロセス

図を使って例を考えてみましょう

空のセットから訪問頂点の監視を開始

リーリー

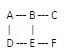
指定された条件に基づいて配列から構築されたグラフにサイクルが含まれているかどうかを確認します

ループ検出プロセスの開始点として任意の頂点を選択します。頂点 A を選択します。

現在の頂点 (A) の隣接する頂点を確認します。この例では、A の近隣者は B と D です。これらをアクセスセットに追加し、A をその親ノードとして識別します

B は、アクセスセット内の次のアクセス頂点です。

B の周囲を探索してください。 B のすぐ隣の人は A、C、E です。 A はすでに訪問頂点セット内にありますが、B の親ではないため、サイクルを形成しません。

次に訪問する頂点 D に進みます。

Dの知り合いを発見。 A と E は D の最近傍です。 A はすでにアクセスセットに含まれており、D の親であるため、D をその親に接続するエッジ (D -> A) が存在する必要があります。これは、グラフにサイクルが含まれていることを示します。

プロセスはここで終了します。BFS を使用してグラフ内のループを検出することに成功しました。つまり (A->B->E->D->A) です。

要約すると、多くのアプリケーションでは、指定されたパラメーターに基づいて配列から構築されたグラフ内のループを見つけられることが重要です。 DFS と BFS のどちらを使用する場合でも、このプロセスは、ループの可能性を見つけて、ネットワーク、回線、および関係に関する現実の問題を解決するのに役立ちます。効果的なループ検出により、アルゴリズムの速度が向上し、データが正しいことを確認できます。

以上が指定された条件に基づいて配列から構築されたグラフにサイクルが含まれているかどうかを確認しますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。