二分木内の二等辺三角形の数
バイナリ ツリーは、各ノードが最大 2 つの子ノードを持つことができるデータ構造です。これらの子は、それぞれ左の子と右の子と呼ばれます。親の配列表現が与えられたとします。それを使用してバイナリ ツリーを作成する必要があります。二分木には複数の二等辺三角形が含まれる場合があります。この二分木で可能な二等辺三角形の総数を見つけなければなりません。
この記事では、C でこの問題を解決するためのいくつかの手法を検討します。
質問を理解する
親配列を提供します。配列インデックスがツリー ノードの値を形成し、配列内の値がその特定のインデックスの親ノードを与えるように、それをバイナリ ツリーの形式で表す必要があります。
-1 は常にルートの親ノードであることに注意してください。以下に、配列とそのバイナリ ツリー表現を示します。
リーリーバイナリ ツリー -
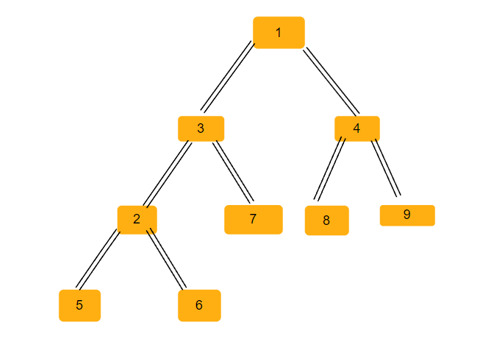
どの二分木でも、3 種類の二等辺三角形を使用できます -
左二等辺三角形 − この三角形では、頂点は left 親ノードの子ノードと底辺(二等辺三角形の両辺)を形成する頂点が頂点の左側の子ノードとなります。子ノードは直接的または間接的です。上のツリーには、そのような二等辺三角形が 2 つあります - (2, 6, 3)、(3, 7, 1)。
右二等辺三角形 − この三角形の頂点は right親の子ですが、ベースを形成する頂点は頂点の正しい子です。子供は直接的または間接的です。上のツリーには、そのような二等辺三角形が 1 つだけあります (4、1、8)。
平衡二等辺三角形 − この三角形では、底辺を形成する頂点が頂点ノードの左右の子ノードです。上のツリーには、そのような二等辺三角形が 5 つあります (1, 3, 4)、(3, 2, 7)、(4, 8, 9)、(2, 5, 6)、(1, 2, 9)
したがって、上記の二分木には、合計 8 個の二等辺三角形 が存在します。
深さ優先検索を使用したトラバーサル
深さ優先検索 (DFS) は、ツリーのすべてのノードを深さ方向に走査する方法です。ルート ノードから開始され、各ブランチに移動し、その後バックトラックします。
まず、DFS を使用してバイナリ ツリーの各ノードを走査し、各ノードが互いに隣接して表現されるようにグラフに変換します。これにより、トラバースが容易になります。
各ノードについて、子ノードがあるかどうかを確認します。確認後、sort(node[x].begin(), node[x].end()) 関数を使用して並べ替えます。
次に、現在のノードが対応する親ノードの左または右の後継ノードであるかどうかを確認します。バイナリ ツリーのすべてのノードで DFS 関数を再帰的に使用します。
現在のノードに 2 つの子がある場合 (直接的または間接的に)、それらの間のエッジを計算することで二等辺三角形が存在する可能性をチェックします。以下のコードにある graph 関数を使用して、それらの間のエッジを見つけます。
最後に、さまざまな位置にあるすべての可能な三角形を合計することで、二等辺三角形の総数を計算します。
親配列が与えられた場合に、二分木内の正三角形の総数を見つける方法について説明しました。これは、二分木を走査できる深さ優先検索を使用することで実現できます。
以上が二分木内の二等辺三角形の数の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7500
7500
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 52
52
 OpenOOD アップデート v1.5: 包括的かつ正確な配布外検出コード ライブラリとテスト プラットフォーム、オンライン ランキングとワンクリック テストをサポート
Jul 03, 2023 pm 04:41 PM
OpenOOD アップデート v1.5: 包括的かつ正確な配布外検出コード ライブラリとテスト プラットフォーム、オンライン ランキングとワンクリック テストをサポート
Jul 03, 2023 pm 04:41 PM
配布外 (OOD) の検出は、オープンワールドのインテリジェント システムの信頼性の高い動作に不可欠ですが、現在のオブジェクト指向の検出方法では「評価の不一致」(評価の不一致) が発生します。以前の作品 OpenOODv1 は OOD 検出の評価を統合しましたが、スケーラビリティと使いやすさには依然として制限がありました。最近、開発チームは OpenOODv1.5 を再度提案し、以前のバージョンと比較して、新しい OOD 検出手法の評価は、精度の確保、標準化、使いやすさの点で大幅に改善されました。イメージペーパー: https://arxiv.org/abs/2306.09301OpenOODCodebase:htt
 知識を増やしましょう!論理ルールを使用した機械学習
Apr 01, 2023 pm 10:07 PM
知識を増やしましょう!論理ルールを使用した機械学習
Apr 01, 2023 pm 10:07 PM
適合率-再現率曲線では、同じ点が異なる軸でプロットされます。警告: 左側の最初の赤い点 (再現率 0%、精度 100%) は 0 ルールに対応します。左側の 2 番目のドットが最初のルール、というように続きます。 Skope-rules は、ツリー モデルを使用してルール候補を生成します。まず、いくつかのデシジョン ツリーを構築し、ルート ノードから内部ノードまたはリーフ ノードまでのパスをルール候補として検討します。これらの候補ルールは、適合率や再現率などの事前定義された基準によってフィルタリングされます。精度と再現率がしきい値を超えるものだけが保持されます。最後に、類似性フィルタリングを適用して、十分な多様性を持つルールを選択します。一般に、スコープ ルールは、それぞれの根本原因を学習するために適用されます。
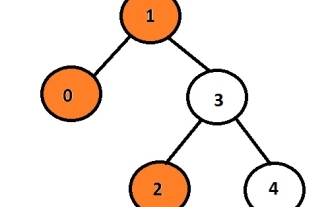 C言語でバイナリツリーの左図を印刷
Sep 03, 2023 pm 01:25 PM
C言語でバイナリツリーの左図を印刷
Sep 03, 2023 pm 01:25 PM
タスクは、指定されたバイナリ ツリーの左ノードを出力することです。まず、ユーザーはデータを挿入してバイナリ ツリーを生成し、結果のツリーの左側のビューを印刷します。各ノードは最大 2 つの子ノードを持つことができるため、このプログラムはノードに関連付けられた左ポインタのみを反復する必要があります。左ポインタが null でない場合は、それに関連付けられたデータまたはポインタがあることを意味します。それ以外の場合は、次のように出力および表示されます。出力の左側の子。例入力:10324出力:102ここで、オレンジ色のノードはバイナリ ツリーの左側のビューを表します。指定されたグラフでは、データ 1 を持つノードがルート ノードであるため、それが出力され、左の子に進む代わりに 0 が出力され、次に 3 に進み、その左の子である 2 が出力されます。再帰的メソッドを使用してノードのレベルを保存できます
 Javaのバイナリツリー構造を詳しく解説
Jun 16, 2023 am 08:58 AM
Javaのバイナリツリー構造を詳しく解説
Jun 16, 2023 am 08:58 AM
バイナリ ツリーは、コンピュータ サイエンスにおける一般的なデータ構造であり、Java プログラミングでも一般的に使用されるデータ構造です。この記事ではJavaのバイナリツリー構造について詳しく紹介します。 1. 二分木とは何ですか?コンピューター サイエンスにおけるバイナリ ツリーは、各ノードが最大 2 つの子ノードを持つツリー構造です。このうち、左側の子ノードは親ノードより小さく、右側の子ノードは親ノードより大きい。 Java プログラミングでは、ソート、検索、およびデータ クエリの効率向上を表すためにバイナリ ツリーが一般的に使用されます。 2. Java でのバイナリ ツリーの実装 Java では、バイナリ ツリー
 Javaのランタイムによって提供されるパラメータの数を確認するにはどうすればよいですか?
Sep 23, 2023 pm 01:13 PM
Javaのランタイムによって提供されるパラメータの数を確認するにはどうすればよいですか?
Sep 23, 2023 pm 01:13 PM
Java では、実行時にパラメータを渡す 1 つの方法は、コマンド ラインまたはターミナルを使用することです。コマンド ライン パラメーターのこれらの値を取得する場合、実行時にユーザーが指定したパラメーターの数を見つける必要がある場合があります。これは、length 属性を使用して実現できます。この記事は、サンプル プログラムを使用して、ユーザーが指定した数のパラメーターを渡したり取得したりするプロセスを説明することを目的としています。実行時にユーザーが指定した引数の数を取得する コマンド ライン引数の数を調べる前に、最初のステップとして、ユーザーが実行時に引数を渡せるようにするプログラムを作成します。 String[] パラメータ Java プログラムを作成するとき、main() メソッドに遭遇することがよくあります。 JVM がこのメソッドを呼び出すと、Java アプリケーションが実行を開始します。 String[]args という引数とともに使用されます。
 Linuxコマンド:Telnetプロセス数の確認方法
Mar 01, 2024 am 11:39 AM
Linuxコマンド:Telnetプロセス数の確認方法
Mar 01, 2024 am 11:39 AM
Linux コマンドは、システム管理者の日常業務に欠かせないツールの 1 つであり、さまざまなシステム管理タスクの実行に役立ちます。運用保守作業では、問題を検出して適時に調整するために、システム内の特定のプロセスの番号を確認する必要がある場合があります。この記事では、Linuxコマンドを使用してTelnetプロセス数を確認する方法を紹介しますので、一緒に学びましょう。 Linux システムでは、ps コマンドと grep コマンドを組み合わせて使用すると、Telnet プロセスの数を表示できます。まず、ターミナルを開く必要があります。
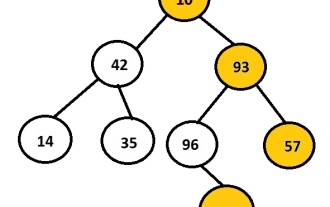 C 言語でバイナリ ツリーの右側のビューを出力します。
Sep 16, 2023 pm 11:13 PM
C 言語でバイナリ ツリーの右側のビューを出力します。
Sep 16, 2023 pm 11:13 PM
タスクは、指定されたバイナリ ツリーの右ノードを出力することです。まずユーザーはデータを挿入してバイナリ ツリーを作成し、次に結果のツリーの右側のビューを印刷します。上の画像は、ノード 10、42、93、14、35、96、57、88 を使用して作成されたバイナリ ツリーを示しており、ツリーの右側のノードが選択されて表示されています。たとえば、10、93、57、および 88 はバイナリ ツリーの右端のノードです。例 入力:1042931435965788出力:10935788 各ノードには、左ポインターと右ポインターの 2 つのポインターがあります。この質問によると、プログラムは正しいノードをトラバースするだけで済みます。したがって、ノードの左側の子を考慮する必要はありません。右側のビューには、階層内の最後のノードであるすべてのノードが保存されます。したがって、できることは、
 C++ を使用して、同じ最小値と最大値を持つ部分配列の数を見つけるコードを作成します。
Aug 25, 2023 pm 11:33 PM
C++ を使用して、同じ最小値と最大値を持つ部分配列の数を見つけるコードを作成します。
Aug 25, 2023 pm 11:33 PM
この記事では、C++ を使用して、最大値と最小値が同じ部分配列の数を求める問題を解決します。以下は問題の例です。 -入力:array={2,3,6,6,2,4,4,4}出力:12説明:{2},{3},{6},{6}, {2 }、{4}、{4}、{4}、{6,6}、{4,4}、{4,4}、および {4,4,4} は、同じ最大要素と最小要素で形成できるサブ配列です。入力: 配列 = {3, 3、1、5、




