C プログラムでの LCS のスペースを最適化したソリューション?

ここでは、LCS 問題の空間最適化手法を見ていきます。 LCS は最長の共通部分列です。 2 つの文字列が「BHHUBC」と「HYUYBZC」の場合、サブシーケンスの長さは 4 です。動的プログラミング手法はすでにその 1 つですが、動的プログラミング手法を使用するとさらに多くのスペースが必要になります。次数 m x n のテーブルが必要です。ここで、m は最初の文字列の文字数、n は 2 番目の文字列の文字数です。
ここでは、O(n) 補助スペースの使用方法を学びます。古いアプローチを見ると、各反復で前の行のデータが必要であることがわかります。すべてのデータが必要なわけではありません。したがって、サイズ 2n のテーブルを作成しても問題ありません。この考え方を理解するためにアルゴリズムを見てみましょう。
アルゴリズム
lcs_problem(X, Y) -
begin
m := length of X
n := length of Y
define table of size L[2, n+1]
index is to point 0th or 1st row of the table L.
for i in range 1 to m, do
index := index AND 1
for j in range 0 to n, do
if i = 0 or j = 0, then
L[index, j] := 0
else if X[i - 1] = Y[j - 1], then
L[index, j] := L[1 – index, j - 1] + 1
else
L[index, j] := max of L[1 – index, j] and L[index, j-1]
end if
done
done
return L[index, n]
end例
#include <iostream>
using namespace std;
int lcsOptimized(string &X, string &Y) {
int m = X.length(), n = Y.length();
int L[2][n + 1];
bool index;
for (int i = 0; i <= m; i++) {
index = i & 1;
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0)
L[index][j] = 0;
else if (X[i-1] == Y[j-1])
L[index][j] = L[1 - index][j - 1] + 1;
else
L[index][j] = max(L[1 - index][j], L[index][j - 1]);
}
}
return L[index][n];
}
int main() {
string X = "BHHUBC";
string Y = "HYUYBZC";
cout << "Length of LCS is :" << lcsOptimized(X, Y);
}出力
Length of LCS is :4
以上がC プログラムでの LCS のスペースを最適化したソリューション?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 1664
1664
 14
14
 1423
1423
 52
52
 1318
1318
 25
25
 1269
1269
 29
29
 1248
1248
 24
24
 以下を中国語に翻訳してください: ローマ数字を 10 進数に変換する C プログラム
Sep 05, 2023 pm 09:53 PM
以下を中国語に翻訳してください: ローマ数字を 10 進数に変換する C プログラム
Sep 05, 2023 pm 09:53 PM
以下に、ローマ数字を 10 進数に変換する C 言語アルゴリズムを示します。 アルゴリズム ステップ 1 - 開始 ステップ 2 - 実行時にローマ数字を読み取る ステップ 3 - 長さ: = strlen(roman) ステップ 4 - i=0 から長さ-1 の場合 ステップ4.1-switch(roman[i]) ステップ 4.1.1-case'm': &nbs
 2 つの文字列の辞書編集上の順序を比較する C++ プログラム
Sep 04, 2023 pm 05:13 PM
2 つの文字列の辞書編集上の順序を比較する C++ プログラム
Sep 04, 2023 pm 05:13 PM
辞書編集的な文字列比較とは、文字列が辞書順に比較されることを意味します。たとえば、「apple」と「appeal」という 2 つの文字列がある場合、「app」の最初の 3 文字が同じであるため、最初の文字列が最後に来ます。次に、最初の文字列の文字は「l」で、2 番目の文字列の 4 番目の文字は「e」になります。 「e」は「l」より短いため、辞書順に並べ替えると最初に表示されます。文字列は配置される前に辞書順に比較されます。この記事では、C++ を使用して 2 つの文字列を辞書編集的に比較するためのさまざまな手法を見ていきます。 C++ 文字列での Compare() 関数の使用 C++string オブジェクトには Compare() があります。
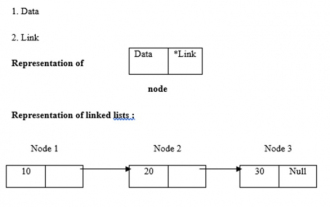 リンクリストの長さを求めるCプログラム
Sep 07, 2023 pm 07:33 PM
リンクリストの長さを求めるCプログラム
Sep 07, 2023 pm 07:33 PM
リンク リストは動的なメモリ割り当てを使用します。つまり、リンク リストはそれに応じて拡大および縮小します。これらはノードのコレクションとして定義されます。ここで、ノードにはデータとリンクという 2 つの部分があります。データ、リンク、リンクリストの表現は以下のとおりです。 ・リンクリストの種類 リンクリストには以下の4種類があります。 ・シングルリンクリスト/シングルリンクリスト ダブル/ダブルリンクリスト 循環シングルリンクリスト 循環ダブルリンクリスト再帰的メソッドを使用してリンク リストの長さを確認します。ロジックは -intlength(node *temp){ if(temp==NULL) returnl; else{&n
 指定された値を引数として受け取る逆双曲線正弦関数の値を見つける C++ プログラム
Sep 17, 2023 am 10:49 AM
指定された値を引数として受け取る逆双曲線正弦関数の値を見つける C++ プログラム
Sep 17, 2023 am 10:49 AM
双曲線関数は、円の代わりに双曲線を使用して定義され、通常の三角関数と同等です。ラジアン単位で指定された角度から双曲線正弦関数の比率パラメーターを返します。しかし、その逆、つまり別の言い方をすればいいのです。双曲線正弦から角度を計算したい場合は、双曲線逆正弦演算のような逆双曲線三角関数演算が必要です。このコースでは、C++ で双曲線逆サイン (asinh) 関数を使用し、ラジアン単位の双曲線サイン値を使用して角度を計算する方法を説明します。双曲線逆正弦演算は次の式に従います -$$\mathrm{sinh^{-1}x\:=\:In(x\:+\:\sqrt{x^2\:+\:1})}ここで\:In\:is\:自然対数\:(log_e\:k)
 C プログラムは rename() 関数を使用してファイル名を変更します
Sep 21, 2023 pm 10:01 PM
C プログラムは rename() 関数を使用してファイル名を変更します
Sep 21, 2023 pm 10:01 PM
名前変更機能は、ファイルまたはディレクトリを古い名前から新しい名前に変更します。この操作は移動操作と似ています。したがって、この名前変更機能を使用してファイルを移動することもできます。この関数は、stdio.h ライブラリ ヘッダー ファイルに存在します。 rename 関数の構文は次のとおりです: intrename(constchar*oldname,constchar*newname); rename() 関数は 2 つのパラメータを受け取ります。 1 つは古い名前、もう 1 つは新しい名前です。どちらのパラメータも、ファイルの古い名前と新しい名前を定義する定数文字へのポインタです。ファイルの名前が正常に変更された場合はゼロを返し、それ以外の場合はゼロ以外の整数を返します。名前変更操作中
 指定された複素数の虚数部を取得する C++ プログラム
Sep 06, 2023 pm 06:05 PM
指定された複素数の虚数部を取得する C++ プログラム
Sep 06, 2023 pm 06:05 PM
現代科学は、複数の数の概念に大きく依存しています。この概念は、17 世紀初頭にジローラモ カルダーノによって初めて確立され、16 世紀に導入されました。複素数の公式は a+ib です。ここで、a は HTML コードを保持し、b は実数です。複素数には、実数部 <a> と虚数部 (<ib>) の 2 つの部分があると言われます。 i または iota の値は √-1 です。 C++ の複数形クラスは、複素数を表すために使用されるクラスです。 C++ の複合クラスは、いくつかの複素数演算を表現および制御できます。複数の数値を表現し、表示を制御する方法を見てみましょう。 imag() メンバー関数 上で述べたように、複素数は実数部と虚数部で構成されます。実数部を表示するには、real() を使用します。
 辞書を印刷する C++ プログラム
Sep 11, 2023 am 10:33 AM
辞書を印刷する C++ プログラム
Sep 11, 2023 am 10:33 AM
マップは C++ の特別なタイプのコンテナで、各要素は 2 つの値、つまりキー値とマップ値のペアです。キー値は各項目のインデックス付けに使用され、マップされた値はキーに関連付けられた値です。マップされた値が一意であるかどうかに関係なく、キーは常に一意です。 C++ でマップ要素を出力するには、反復子を使用する必要があります。項目のセット内の要素は、反復子オブジェクトによって示されます。イテレータは主に配列や他のタイプのコンテナ (ベクトルなど) で使用され、特定の範囲内の特定の要素を識別するために使用できる特定の操作セットを備えています。イテレータをインクリメントまたはデクリメントして、範囲またはコンテナ内に存在するさまざまな要素を参照できます。イテレータは、範囲内の特定の要素のメモリ位置を指します。イテレータを使用して C++ でマップを出力する まず、定義方法を見てみましょう。
 文字がアルファベットか非アルファベットかをチェックする C++ プログラム
Sep 14, 2023 pm 03:37 PM
文字がアルファベットか非アルファベットかをチェックする C++ プログラム
Sep 14, 2023 pm 03:37 PM
論理プログラミングの問題を解決する場合、文字列または文字の使用が非常に役立つ場合があります。文字列は文字の集合であり、ASCII 値の記号を保持するために使用される 1 バイトのデータ型です。記号には、英文字、数字、または特殊文字を使用できます。この記事では、C++ を使用して文字が英語文字かアルファベット文字かを確認する方法を学びます。 isalpha() 関数のチェック 数値が文字であるかどうかをチェックするには、ctype.h ヘッダー ファイルの isalpha() 関数を使用できます。これは文字を入力として受け取り、それがアルファベットの場合は true を返し、そうでない場合は false を返します。この関数の使用法を理解するために、次の C++ 実装を見てみましょう。 Example の中国語訳は次のとおりです。




