階乗 n を連続する数値の合計として表現します

数値の階乗を連続する数値の合計として表現する方法を見つけるための 2 つの方法について説明します。最初の方法は直接的で単純な方法ですが、もう 1 つの方法では等差数列の概念を使用して、占有される時間と空間の点で複雑さを軽減します。
###問題文###数値が与えられた場合、その数値の階乗を連続する自然数の合計として表現する方法を見つける必要があります。
これには 2 つの異なる機能が関係します -
- 数値の階乗を求めます。
-
誰もが知っているように、3 の階乗は 6 であり、1 2 3 と書くことができるため、答えは 1 通りです。
例 2
リーリー誰もが知っているように、4 の階乗は 24 で、7 8 9 と書くことができるため、答えは 1 通りです。
方法1
これは単純な方法です。まず数値の階乗を求め、それを連続する自然数の和として表現できる方法の数を計算します。この方法は、階乗を一連の算術長さ len 1 として -
のように表現することです。 リーリーlen を正の整数として取得した場合、それを解として扱います。
###例###次の例では、数値の階乗を連続する数値の合計として表現する方法の数を求めます。
リーリー ###出力###上記の C プログラムを実行すると、次の出力が生成されます -
リーリー方法 2: 最適化方法
これはより良いアプローチです。上記のアプローチではオーバーフローが発生します。
数値 p から始まる len 個の連続する数値の合計は、 -
と書くことができます。 リーリー sumも Number! に等しいためです。
###我々は書ける### リーリーここでは、すべての (len, p) ペアを数えるのではなく、すべての (len, (len 2*p 1)) ペアを数えます。これは、AB=2*Number であるすべての順序付けされた pf (A, B) を計算することを意味します。そしてA
これは、2*数値の奇数の約数を探していることを意味します。これは Number の奇数の約数でもあります。 約数の数を計算するには! 、因数分解では素数の累乗を計算する必要があり、約数の数は (f1 1)*(f2 1)* … *(fn 1) となります。
ルジャンドルの公式を使用して、数値の階乗における素数の最大累乗を計算します。
###例###このアプローチのコードを以下に示します - リーリー ###出力###
上記の C プログラムを実行すると、次の出力が生成されます -
リーリー ###結論は###この記事では、数値の階乗を連続する自然数の合計として表現する、数値を求める 2 つの異なる方法について説明しました。
以上が階乗 n を連続する数値の合計として表現しますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7467
7467
 15
15
 1376
1376
 52
52
 77
77
 11
11
 18
18
 19
19
 Python のタプルの絶対和
Sep 12, 2023 pm 07:37 PM
Python のタプルの絶対和
Sep 12, 2023 pm 07:37 PM
Python では、タプルは、異なる型の複数の要素を格納できる不変のシーケンスです。これらは、関連する値のコレクションを表すためによく使用されます。タプルの合計には、2 つ以上のタプルの対応する要素を加算して新しいタプルを生成することが含まれます。ただし、シナリオによっては、従来の合計ではなく要素の絶対合計を計算する必要がある場合があります。このブログ投稿では、Python でタプルの絶対和を実行する方法を検討します。従来のタプル合計 絶対的なタプル合計について詳しく説明する前に、まず従来のタプル合計の実行方法を理解しましょう。同じ長さの 2 つのタプルがある場合、単純な Python ループまたはリスト内包表記を使用して、対応する要素の合計 -deftuple_sum(t1,t2) を計算できます。
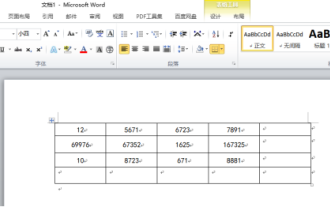 Wordの表を合計する方法を知っていますか?
Mar 21, 2024 pm 01:10 PM
Wordの表を合計する方法を知っていますか?
Mar 21, 2024 pm 01:10 PM
Word の表で数を数えるという問題に遭遇することがあります。通常、このような問題に遭遇すると、ほとんどの生徒は Word の表を Excel にコピーして計算しますが、黙って電卓を手に取る生徒もいます。簡単に計算する方法はありますか?もちろんありますが、実はWordでも合計額を計算することができます。それで、その方法を知っていますか?今日は、一緒に見ていきましょう!困っている友達はすぐに集めてください。手順の詳細: 1. まず、コンピューターで Word ソフトウェアを開き、処理する必要がある文書を開きます。 (図のように) 2. 次に、(図のように) 合計値が配置されているセルにカーソルを置き、[メニュー バー] をクリックします。
 交互に配置された符号の等差数列の合計を求めます。
Sep 16, 2023 pm 05:01 PM
交互に配置された符号の等差数列の合計を求めます。
Sep 16, 2023 pm 05:01 PM
等差数列 (AP) は、連続する 2 つの項の差が同じである一連の数値です。差は、第 1 項から第 2 項を減算して計算されます。シーケンス 5,7,9,11,13,15,... の例を使用して AP を理解しましょう。この等差級数の許容誤差 (d) は 2 です。これは、後続の各要素が前の要素と 2 だけ異なることを意味します。このシーケンスの最初の項目 (a) は 5 です。 n 番目の項を見つけるための一般式は、a{n}=a+(n-1)(d) です。 この問題では、AP が与えられ、一連の交互に符号付き正方形の合計を見つける必要があります。その系列は次のようになります。以下に示すように、a12-a22+a32-a42+a52+... より明確に理解するために例を見てみましょう。
 PHP の array_sum() 関数を使用して、配列内の要素の合計を求めます。
Nov 18, 2023 am 11:20 AM
PHP の array_sum() 関数を使用して、配列内の要素の合計を求めます。
Nov 18, 2023 am 11:20 AM
タイトル: PHP の array_sum() 関数を使用して配列要素の合計を求める PHP は、開発プロセスを簡素化し効率を向上させる多数の組み込み関数を提供する、広く使用されているサーバーサイド スクリプト言語です。その中でも、array_sum()関数は、配列内の要素の合計を計算するために使用できる非常に実用的な関数です。この記事では、array_sum() 関数の使用方法を学び、具体的なコード例を示します。まず、array_sum() 関数の使用法を理解する必要があります。
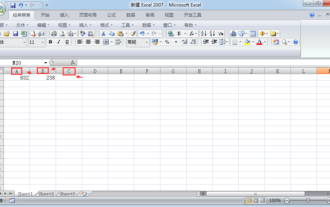 Excelで自動的に合計を計算する方法
Mar 20, 2024 pm 12:20 PM
Excelで自動的に合計を計算する方法
Mar 20, 2024 pm 12:20 PM
Excel の表を頻繁に使用するユーザーにとって、自動合計機能は非常に簡単な操作で、ニーズに応じて小数点以下数桁まで自動的に合計できるため、手動で電卓を押すよりもはるかに便利です。初心者ユーザーにとって、Excel で合計を自動的に合計する方法を最初から学ぶ必要があります。手順を見てみましょう: Excel の自動合計: まず、セル A1 とセル B1 の数値を加算し、結果をセルに表示する必要があります。セルC1。これを行うには、まずセル A1 と B1 に追加する数値を入力します。次に、セル C1 を選択し、次の数式を入力します: `=A1+B1` Enter キーを押すと、セル C1 にはセル A1 と B1 の数値の合計が表示されます。
 Go言語の配列関数を使用して結果を合計して返すにはどうすればよいですか?
Jul 31, 2023 pm 02:25 PM
Go言語の配列関数を使用して結果を合計して返すにはどうすればよいですか?
Jul 31, 2023 pm 02:25 PM
Go言語の配列関数を使用して結果を合計して返すにはどうすればよいですか? Go 言語には、配列要素の合計を求める関数など、豊富な配列演算関数が用意されています。これらの関数を使用すると、配列に対して合計演算を簡単に実行し、結果を返すことができます。この記事では、Go言語の配列関数を使って合計して結果を返す方法をコード例を交えて紹介します。まず、Go 言語の配列を見てみましょう。配列は、固定サイズの要素シーケンスを格納するデータ構造です。 Go言語では配列の長さは固定であり、配列の型と要素は
 Excelの合計数式の使い方 - Excelの合計数式の使い方のチュートリアル
Mar 05, 2024 pm 12:40 PM
Excelの合計数式の使い方 - Excelの合計数式の使い方のチュートリアル
Mar 05, 2024 pm 12:40 PM
Excel の合計数式の使い方をまだ知らない友人も多いため、以下のエディターで Excel の合計数式の使用方法について説明しています。必要な場合は、ご覧ください。みんな。ステップ 1: まず、Excel を開きます (図を参照)。ステップ 2: Excel 作業インターフェイスに入ります (図を参照)。ステップ 3: 次に、編集する必要があるドキュメントを開きます (図に示すように) サンプルドキュメントは次のとおりです。ステップ 4: 「Total Score」を選択し、fx 関数ボックスに「=C2+D2+E2」と入力し、Enter キーを押します。合計スコアが出ます(写真の通り)。ステップ 5: 入力ボックスのドロップダウン メニューをクリックします。合計スコアを入力します (図を参照)。ステップ 6: ドロップダウンに入力します (図を参照)。ステップ 7:
 数値の合計を出力する Java プログラム
Aug 20, 2023 am 09:49 AM
数値の合計を出力する Java プログラム
Aug 20, 2023 am 09:49 AM
Java には数値を追加するさまざまな方法があります。追加する数値は実行時に入力することも、プログラム内に直接入力することもできます。ただし、数値のリストが大きすぎる場合、この方法で数値を追加するのは困難です。追加するデータが Excel スプレッドシート/g で指定される場合もあります。




