直角三角形の外接円の面積はいくらですか?

直角三角形の斜辺(H)が与えられたとき、式πH²/4を使って直角三角形の外接円の面積を求めます。

この公式は、外接円が三角形のすべての角に接するという事実を利用して導出されます。この場合、円の中心を通過する 2 点間の仮想的な最大長です。これにより、斜辺が円の直径になります。

これが、円の面積が πd²/4 となる理由です。 (d = 2r) d を H に置き換えます。

例

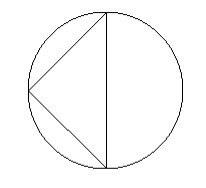
斜辺 = 8

円面積 = 50.26

コード例

ライブデモ

#include <stdio.h>
int main(void) {
   int H = 14;
   float pie = 3.14;
   float area = (float)((pie*H*H)/4);
   printf("the area of circumcircle of a right angled triangle of Hypotenuse %d is %f",H,area);
   return 0;
}

出力

the area of circumcircle of a right angled triangle of Hypotenuse 14 is 153.860016

以上が直角三角形の外接円の面積はいくらですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。