行列の対角の合計を計算する C++ プログラム

2 次元配列または行列の利用は、いくつかの場合に非常に有利です。 行列の行と列は数値を保持するために使用されます。2D を定義できます。 多次元配列は、C で行列を表すために使用されます。この記事では、その実装方法について説明します C を使用して、指定された正方行列の対角和を計算します。
行列には、主対角と副対角という 2 つの対角があります (場合によっては 主対角線と副対角線と呼ばれます)。主対角線は左上から始まります。 隅 (インデックス [0, 0]) から右下隅 (インデックス [n-1, n-1]) まで。n は順序です。 正方行列。主対角線は右上隅 (インデックス [n-1, 0]) から始まり、左下隅で終わります。 コーナー (インデックス [0, n-1]). 要素の合計を求めるアルゴリズムを見てみましょう。 これら 2 つの対角線。
行列の対角の和
の中国語訳は次のとおりです:行列の対角の和
$$\begin{bmatrix} 8 & 5& 3\改行 6 & 7& 1\改行 2&4&9\ \end{bmatrix},$$
リーリー前の例では、1 つの 3 x 3 行列が使用され、対角線をスキャンしました。 明確に理解するために、アルゴリズムと実装を見てみましょう。 ビュー。### ###アルゴリズム###
行列 M を入力として読み取ります
- n行n列のMを考えてみましょう
- 合計メジャー := 0
- 合計_マイナー := 0
- i の範囲が 0 から n-1 の場合、
- を実行します。
- j の範囲が 0 から n - 1 の場合、次のようにします。
-
- sum_major := sum_major M[ i ][ j ]
-
- 終了 if
if (i j) が (N - 1) と同じである場合、
- sum_minor := sum_minor M[ i ][ j ]
-
- 終了 if
- 終了
-
- 終了
- ###例### リーリー ###出力### リーリー ###結論###
- この記事では、与えられた正方行列の対角和を計算する方法について説明しました。 主対角線は左上隅から右下隅まで延び、副対角線は左下隅から右上隅まで延びます。 対角線は右上隅から左下隅まで始まります。これらの合計を求めるには 対角要素の場合、すべての要素をループします。行と列の両方のインデックス値が値である場合、 同様に、2 つのインデックスの合計が次の場合に主対角要素を表します。 行列の次数 n-1 と同じように、下対角に追加されます。 プロシージャは 2 つのネストされたループを使用し、プロシージャ内に存在するすべての要素を調べます。 2次元配列。したがって、2 つの対角線の合計を計算するには O(n 2
- i と j が同じ場合、
以上が行列の対角の合計を計算する C++ プログラムの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7480
7480
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 33
33
 GoogleマップをiPhoneのデフォルト地図にする方法
Apr 17, 2024 pm 07:34 PM
GoogleマップをiPhoneのデフォルト地図にする方法
Apr 17, 2024 pm 07:34 PM
iPhone のデフォルトの地図は、Apple 独自の地理位置情報プロバイダーである Maps です。マップは改善されていますが、米国外ではうまく機能しません。 Googleマップと比べて何も提供するものはありません。この記事では、Google マップを iPhone のデフォルトの地図として使用するための実行可能な手順について説明します。 Google マップを iPhone のデフォルトの地図にする方法 Google マップを携帯電話のデフォルトの地図アプリとして設定するのは、思っているよりも簡単です。以下の手順に従ってください – 前提条件 – 携帯電話に Gmail がインストールされている必要があります。ステップ 1 – AppStore を開きます。ステップ 2 – 「Gmail」を検索します。ステップ 3 – Gmail アプリの横にある をクリックします
 CUDA の汎用行列乗算: 入門から習熟まで!
Mar 25, 2024 pm 12:30 PM
CUDA の汎用行列乗算: 入門から習熟まで!
Mar 25, 2024 pm 12:30 PM
General Matrix Multiplication (GEMM) は、多くのアプリケーションやアルゴリズムの重要な部分であり、コンピューター ハードウェアのパフォーマンスを評価するための重要な指標の 1 つでもあります。 GEMM の実装に関する徹底的な調査と最適化は、ハイ パフォーマンス コンピューティングとソフトウェア システムとハードウェア システムの関係をより深く理解するのに役立ちます。コンピューター サイエンスでは、GEMM を効果的に最適化すると、計算速度が向上し、リソースが節約されます。これは、コンピューター システムの全体的なパフォーマンスを向上させるために非常に重要です。 GEMM の動作原理と最適化方法を深く理解することは、最新のコンピューティング ハードウェアの可能性をより有効に活用し、さまざまな複雑なコンピューティング タスクに対してより効率的なソリューションを提供するのに役立ちます。 GEMMのパフォーマンスを最適化することで
 Word文書で足し算、引き算、掛け算、割り算を計算する方法
Mar 19, 2024 pm 08:13 PM
Word文書で足し算、引き算、掛け算、割り算を計算する方法
Mar 19, 2024 pm 08:13 PM
WORD は強力なワード プロセッサです。Word を使用してさまざまなテキストを編集できます。Excel の表では、足し算、引き算、乗算の計算方法をマスターしました。そのため、Word の表で数値の足し算を計算する必要がある場合は、乗数を引くにはどうすればよいですか? 計算には電卓しか使用できませんか?答えはもちろん「いいえ」です。WORD でも実行できます。今日は、Word文書の表で加算、減算、乗算、除算などの基本的な演算を数式を使って計算する方法を説明しますので、一緒に学びましょう。そこで、今日は、WORD 文書で加算、減算、乗算、除算を計算する方法を詳しく説明します。ステップ 1: WORD を開き、ツールバーの [挿入] の下にある [表] をクリックし、ドロップダウン メニューに表を挿入します。
 C++ で簡単なカウントダウン プログラムを作成するにはどうすればよいですか?
Nov 03, 2023 pm 01:39 PM
C++ で簡単なカウントダウン プログラムを作成するにはどうすればよいですか?
Nov 03, 2023 pm 01:39 PM
C++ は広く使用されているプログラミング言語で、カウントダウン プログラムを作成するのに非常に便利で実用的です。カウントダウン プログラムは、非常に正確な時間計算とカウントダウン機能を提供する一般的なアプリケーションです。この記事では、C++ を使用して簡単なカウントダウン プログラムを作成する方法を紹介します。カウントダウン プログラムを実装する鍵は、タイマーを使用して時間の経過を計算することです。 C++ では、time.h ヘッダー ファイル内の関数を使用してタイマー関数を実装できます。以下は、単純なカウントダウン プログラムのコードです。
 iPhoneに時計アプリがない:それを修正する方法
May 03, 2024 pm 09:19 PM
iPhoneに時計アプリがない:それを修正する方法
May 03, 2024 pm 09:19 PM
携帯電話に時計アプリがありませんか?日付と時刻は iPhone のステータス バーに引き続き表示されます。ただし、時計アプリがないと、世界時計、ストップウォッチ、目覚まし時計、その他多くの機能を使用できません。したがって、見つからない時計アプリを修正することは、やるべきことリストの一番上に置く必要があります。これらの解決策は、この問題の解決に役立ちます。解決策 1 – 時計アプリを配置する 誤って時計アプリをホーム画面から削除した場合は、時計アプリを元の場所に戻すことができます。ステップ 1 – iPhone のロックを解除し、App ライブラリ ページに到達するまで左にスワイプを開始します。ステップ 2 – 次に、検索ボックスで「時計」を検索します。ステップ 3 – 検索結果に以下の「時計」が表示されたら、それを長押しして、
 タスク スケジューラを使用して Web サイトを開く方法
Oct 02, 2023 pm 11:13 PM
タスク スケジューラを使用して Web サイトを開く方法
Oct 02, 2023 pm 11:13 PM
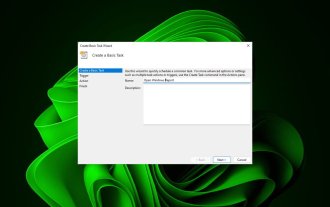
毎日ほぼ同じ時間に同じ Web サイトに頻繁にアクセスしますか?これにより、日常のタスクを実行する際に、複数のブラウザー タブを開いたまま長時間を費やし、ブラウザーが乱雑になる可能性があります。では、ブラウザを手動で起動せずに開いてみてはどうでしょうか?以下に示すように、これは非常にシンプルで、サードパーティのアプリをダウンロードする必要はありません。 Web サイトを開くためにタスク スケジューラを設定するにはどうすればよいですか?キーを押し、検索ボックスに「タスク スケジューラ」と入力し、[開く] をクリックします。 Windows 右側のサイドバーで、「基本タスクの作成」オプションをクリックします。 「名前」フィールドに、開きたい Web サイトの名前を入力し、「次へ」をクリックします。次に、「トリガー」で「時間頻度」をクリックし、「次へ」をクリックします。イベントを繰り返す時間を選択し、「次へ」をクリックします。有効を選択します
 Python の count() 関数を使用してリスト内の要素の数を数える方法
Nov 18, 2023 pm 02:53 PM
Python の count() 関数を使用してリスト内の要素の数を数える方法
Nov 18, 2023 pm 02:53 PM
Python の count() 関数を使用してリスト内の要素の数を計算する方法には、特定のコード サンプルが必要です。Python は強力で習得しやすいプログラミング言語として、さまざまなデータ構造を処理するための組み込み関数を多数提供しています。その 1 つは count() 関数で、リスト内の要素の数をカウントするために使用できます。この記事では、count()関数の使い方と具体的なコード例を詳しく説明します。 count() 関数は Python の組み込み関数であり、特定の値を計算するために使用されます。
 iOS 17: メッセージ内で iMessage アプリを整理する方法
Sep 18, 2023 pm 05:25 PM
iOS 17: メッセージ内で iMessage アプリを整理する方法
Sep 18, 2023 pm 05:25 PM
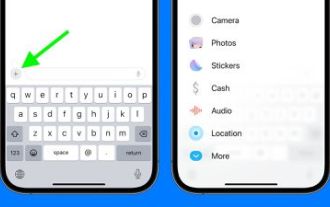
iOS 17 では、Apple はいくつかの新しいメッセージング機能を追加しただけでなく、メッセージ アプリのデザインを微調整して見た目をすっきりさせました。キーボードの上、テキスト入力フィールドの左側にある「+」ボタンをタップすることで、カメラや写真のオプションなど、すべての iMessage アプリとツールにアクセスできるようになりました。 「+」ボタンをクリックすると、デフォルトのオプション順序が記載されたメニュー列が表示されます。上から順に、カメラ、写真、ステッカー、現金 (利用可能な場合)、オーディオ、位置情報があります。一番下には「その他」ボタンがあり、これをタップすると、インストールされている他のメッセージング アプリが表示されます (上にスワイプして、この非表示のリストを表示することもできます)。 iMessage アプリを再編成する方法 以下で実行できます




