C++ でのプログラミング、m 個の奇数を持つ部分配列の数を求める

C を使用したことがある場合は、部分配列とは何か、そしてそれがどれほど役立つかを知っているはずです。誰もが知っているように、C では複数の数学的問題を簡単に解決できます。そこで、この記事では、これらの部分配列を使用して C で M 個の奇数の完全な情報を見つける方法を説明します。
この問題では、指定された配列と整数 m で構成されるサブ配列の数を見つける必要があります。ここで、各サブ配列には正確に m 個の奇数が含まれます。このアプローチの簡単な例を次に示します。
Input : array = { 6,3,5,8,9 }, m = 2
Output : 5
Explanation : Subarrays with exactly 2 odd numbers are
{ 3,5 }, { 6,3,5 }, { 3,5,8 }, { 5,8,9 }, { 6,3,5,8 }, { 3,5,8,9 }
Input : array = { 1,6,3,2,5,4 }, m = 2
Output : 6
Explanation : Subarrays with exactly 2 odd numbers are
{ 1,6,3 }, { 3,2,5 }, { 1,6,3,2 }, { 6,3,2,5 }, { 3,2,5,4 }, { 6,3,2,5,4 }最初のアプローチ
このアプローチでは、すべての可能なサブ配列が指定された配列から生成され、各サブ配列がチェックされます。 m の奇数。これは、時間計算量が O(n2) の単純な生成および検索方法です。
例
#include <bits/stdc++.h>
using namespace std;
int main (){
int a[] = { 1, 6, 3, 2, 5, 4 };
int n = 6, m = 2, count = 0; // n is size of array, m numbers to be find in subarrays,
// count is number of subarray with m odd numbers
for (int i = 0; i < n; i++){ // outer loop to process each element.
int odd = 0;
for (int j = i; j < n; j++) {// inner loop to find subarray with m number
if (a[j] % 2)
odd++;
if (odd == m) // if odd numbers become equals to m.
count++;
}
}
cout << "Number of subarrays with n numbers are: " << count;
return 0;
}出力
Number of subarrays with n numbers are: 6
上記のコードの説明
このコードでは、ネストされたループを使用して、m 個の奇数の部分配列 (外側のループ) を見つけます。 「i」をインクリメントするために使用され、配列内の各要素を処理するために使用されます。
内部ループは、サブ配列を検索し、奇数カウンタが m に達するまで要素を処理するために使用され、見つかった各サブ配列の結果カウンタ カウントをインクリメントし、最後に count
Second に格納された結果を出力します。 1 つのアプローチ
もう 1 つのアプローチは、「i」個の奇数プレフィックスを格納する配列を作成し、各要素を処理して、奇数が見つかるたびに奇数の数をインクリメントすることです。
奇数の数が m を超える場合は、プレフィックス配列の (奇数 - m) 位置の数値をそれに加えます。
奇数が m 以上になると、インデックスと「奇数 - m」の数値が count 変数に追加されるまで、形成された部分配列の数をカウントします。各要素が処理された後、結果は count 変数に格納されます。
例
#include <bits/stdc++.h>
using namespace std;
int main (){
int array[ ] = { 1, 6, 3, 2, 5, 4 };
int n = 6, m = 2, count = 0, odd = 0, i;
int prefix_array[n + 1] = { 0 };
// outer loop to process every element of array
for (i = 0; i < n; i++){
prefix_array[odd] = prefix_array[odd] + 1; // implementing value at odd index in prefix_array[ ]
// if array element is odd then increment odd variable
if (array[i] % 2 == 0)
odd++;
// if Number of odd element becomes equal or greater than m
// then find the number of possible subarrays that can be formed till the index.
if (odd >= m)
count += prefix_array[odd - m];
}
cout << "Number of subarrays with n numbers are: " << count;
return 0;
}出力
Number of subarrays with n numbers are: 6
上記のコードの説明
配列と変数を開始値で初期化する -
int array[ 6 ] = { 1, 6, 3, 2, 5, 4 };
int n = 6, m = 2, count = 0, odd = 0, i;
int prefix_array[n + 1] = { 0 };ここで、変数 n を配列のサイズで初期化し、m を検索する奇数の数で初期化し、可能性のある部分配列の数を保持するために count を 0 で初期化し、奇数を 0 で初期化し、変数 n 0 を prefix_array で初期化します。サイズ n 1 の .
ループについて
for (i = 0; i < n; i++){
prefix_array[odd] = prefix_array[odd] + 1;
if (array[i] % 2 == 0)
odd++;
if (odd >= m)
count += prefix_array[odd - m];
}このループでは、prefix_array[] の奇数インデックスに値を実装し、奇数が見つかった場合は奇数変数をインクリメントします。奇数変数が m 以上の場合、インデックスまでの数の部分配列を形成できることがわかります。
最後に、count 変数に格納されている m 個の奇数の部分配列番号を出力し、出力を取得します。
結論
この記事では、2 つの方法を通じて m 個の奇数部分配列の数を見つける方法について学びました。
各部分を生成する。配列配列を作成し、その中に m 個の奇数があるかどうかを確認し、見つかった各サブ配列のカウントをインクリメントします。このコードの時間計算量は O(n2) です。
効率的な方法は、配列の各要素を反復処理してプレフィックス配列を作成し、プレフィックス配列の助けを借ります。このコードの時間計算量は O(n) です。
この記事が問題と解決策の理解に役立つことを願っています。
以上がC++ でのプログラミング、m 個の奇数を持つ部分配列の数を求めるの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7554
7554
 15
15
 1382
1382
 52
52
 83
83
 11
11
 28
28
 96
96
 C++ を使用して N 番目の非平方数を見つけるコードを作成する
Aug 30, 2023 pm 10:41 PM
C++ を使用して N 番目の非平方数を見つけるコードを作成する
Aug 30, 2023 pm 10:41 PM
私たちは皆、2、3、5、7、8 など、数の 2 乗ではない数字を知っています。非正方形の数は N 個あり、すべての数を知ることは不可能です。そこで、この記事では、平方なしまたは非平方数と、C++ で N 番目の非平方数を見つける方法についてすべて説明します。 N 番目の非平方数 数値が整数の 2 乗である場合、その数値は完全平方と呼ばれます。完全平方数の例としては、-1issquareof14issquareof29issquareof316issquareof425issquareof5 などがあります。数値がどの整数の平方でもない場合、その数値は非正方形と呼ばれます。たとえば、最初の 15 個の非平方数は -2、3、5、6 です。
 Cプログラミングで円の面積を求める
Aug 25, 2023 pm 10:57 PM
Cプログラミングで円の面積を求める
Aug 25, 2023 pm 10:57 PM
円は閉じた図形です。円上のすべての点は、円内の点から等距離にあります。中心点を円の中心といいます。点から円の中心までの距離を半径といいます。面積は、閉じた図形の寸法の範囲を定量的に表現したものです。円の面積は、円の寸法内に囲まれた面積です。円の面積を計算する式、Area=π*r*r 面積を計算するには、円の半径を入力として与え、その式を使用して面積を計算します。アルゴリズム STEP1: stdinput を使用してユーザーからの入力として半径を取得します。STEP2 : area=( を使用して円の面積を計算します。
 C++で書かれた配列の右回転のための反転アルゴリズム
Sep 08, 2023 pm 08:17 PM
C++で書かれた配列の右回転のための反転アルゴリズム
Sep 08, 2023 pm 08:17 PM
この記事では、指定された配列を k 要素分右に回転する逆転アルゴリズムについて学びます。たとえば、−Input:arr[]={4,6,2,6,43,7,3,7}、 k= 4出力:{43,7,3,7,4,6,2,6}説明:配列の各要素を 4 要素ずつ右に回転すると、{43,7,3,7,4,6,2,6} が得られます。入力:arr[]= {8 ,5,8,2,1,4,9,3},k=3出力:{4,9,3,8,5,8,2,1} 解決策を見つける
 C++ を使用して配列内の一意のペアの数を見つける
Sep 07, 2023 am 11:53 AM
C++ を使用して配列内の一意のペアの数を見つける
Sep 07, 2023 am 11:53 AM
C++ の配列構文でいくつかの一意のペアを作成するには、適切な知識が必要です。一意のペアの数を見つけるときに、指定された配列内のすべての一意のペアを数えます。つまり、各ペアが一意である必要がある場所で、考えられるすべてのペアが形成される可能性があります。例: -Input:array[]={5,5,9}Output:4説明:すべての一意のペアの数は(5,5)、(5,9)、(9,5)、および(9,9)です。入力:array[] = {5,4,3,2,2}出力:解決策を見つける16の方法 この問題を解決するには2つの方法があります。
 C++ を使用して、同じ最小値と最大値を持つ部分配列の数を見つけるコードを作成します。
Aug 25, 2023 pm 11:33 PM
C++ を使用して、同じ最小値と最大値を持つ部分配列の数を見つけるコードを作成します。
Aug 25, 2023 pm 11:33 PM
この記事では、C++ を使用して、最大値と最小値が同じ部分配列の数を求める問題を解決します。以下は問題の例です。 -入力:array={2,3,6,6,2,4,4,4}出力:12説明:{2},{3},{6},{6}, {2 }、{4}、{4}、{4}、{6,6}、{4,4}、{4,4}、および {4,4,4} は、同じ最大要素と最小要素で形成できるサブ配列です。入力: 配列 = {3, 3、1、5、
 C++ で書かれており、セット上の再帰関係の数を見つけます。
Aug 26, 2023 pm 08:17 PM
C++ で書かれており、セット上の再帰関係の数を見つけます。
Aug 26, 2023 pm 08:17 PM
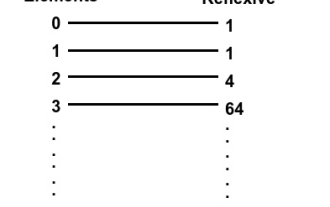
この記事では、セット上の再帰的関係を見つける方法を説明します。この問題では、数値 n と n 個の自然数のセットが与えられ、再帰関係の数を決定する必要があります。再帰的関係 - 集合 A 内のすべての 'a' について (a, a) が関係 R に属している場合、関係 R は集合 A 上の再帰的関係であると言われます。例: -Input:x=1Output:1説明:set={1},reflexiverelationsonA*A:{{1}}Input:x=2Output:4説明:set={1,2},reflexiverelationsonA*
 C++ を使用した指定サイズによる二重リンクリストのグループ化を逆にする
Sep 04, 2023 am 09:49 AM
C++ を使用した指定サイズによる二重リンクリストのグループ化を逆にする
Sep 04, 2023 am 09:49 AM
この問題では、リンクされたリストの先頭へのポインタと整数 k が与えられます。サイズ k のグループでは、リンクされたリストを逆にする必要があります。たとえば、-Input:1<->2<->3<->4<->5(doublelinkedlist),k=3Output:3<->2<->1<->5<->4 解決策を探します方法 この問題では、この問題を解決するための再帰的アルゴリズムを定式化します。この方法では再帰を使用し、再帰を使用して問題を解決します。例#include<iostream&
 C++ で書かれており、最初の 3 項が等差数列で最後の 3 項が等比数列である 4 倍体の数を求めます。
Aug 30, 2023 pm 02:09 PM
C++ で書かれており、最初の 3 項が等差数列で最後の 3 項が等比数列である 4 倍体の数を求めます。
Aug 30, 2023 pm 02:09 PM
この記事では、最初の 3 項に A.P. を使用し、最後の 3 項に G.P. を使用して、クォータニオンを見つけるすべての可能な方法について説明します。まずは等差数列(A.P.)と等比数列(G.P.)の基本的な定義について説明します。等差数列 (A.P.) - 公差 (d) が同じか一定である一連の数値であり、連続する 2 つの数値の差が一定であることを意味します。例: 1,3,5,7,9|d=2 幾何級数 (G.P.) - これは公比 (r) が同じ数列です。つまり、前の数値に固定の乗算ができることを意味します。番号。例: 3, 6, 12, 24, ....|r=2 この問題では、N 個の整数の配列 arr[] にいくつあるかを判断する必要があります。




