回転キャリパー法を使用して、座標平面上の 2 点間の最大距離を計算します。

C には、任意の数値の平方根を返す定義済み関数 sqrt があります。回転キャリパー法は、アルゴリズムまたは計算幾何学を解く際に使用される手法です。

回転キャリパー メソッドの視覚的表現

Hand Rotation は、回転キャリパー プロットの実際の例を示し、手が回転するたびに垂直方向の向きを示します。この概念は、ポリゴンを使用することでも理解できます。

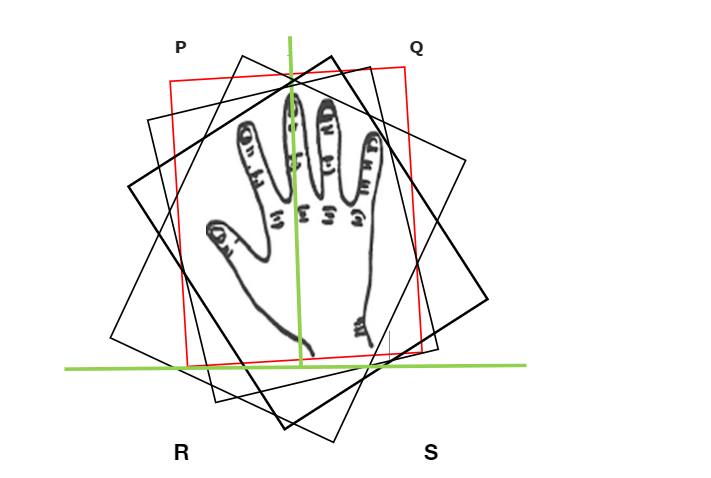
この記事では、回転キャリパー法を使用して 2 つの座標点間の最大距離を見つけます。 跨度>

＃＃＃文法＃＃＃

プログラムでは次の構文を使用します -

リーリー

パラメータ

• ベクトル

  - キーワード ベクトルから始めて、C でベクトルを初期化します。

• datatype

  - ベクトルによって表されるデータ要素のタイプ。

• name

  - ベクトルの名前。

  ＃＃＃アルゴリズム＃＃＃

ヘッダー ファイル

iostream、vector

、
• cmath を使用してプログラムを開始します。
  x
と
• y

  の座標を保存する構造名ポイントを作成しています。 2 つの座標点間の距離を計算するために、double データ型

  distance()
の関数定義を定義しています。ここで、
• Points p1

  と Point p2 は、座標値を受け入れ、事前定義された関数 sqrt と距離公式を使用して距離を返すパラメーターです。 ここでは、

  CP()
という関数定義を定義しています。この double データ型はパラメータ
• Point p1、Point p2、

  Point p3 の計算、外積ベクトルを受け入れます。つまり、x 座標と y 座標に関する p2-p1 および p3-p1 b> です。 今、引数を点ベクトルとして受け取り、任意の 2 つの座標面間の距離を最大化する倍精度データ型

  rotatingCaliper()
の関数定義を作成しています。

• 変数結果を

  0
に初期化します。これは、最大距離の計算を満たすために追跡されます。ポイントのサイズを見つけるには、size() という事前定義された関数を使用し、それを変数 n に保存します。

• 2 つの変数

  j
と
• k

  を 1 に初期化し、次の操作を実行します -

j
をポリゴン内の次の点に移動し、現在のエッジの外積
• 'points[i], Points[

  CP i 1] ] % n'そして、次のエッジ 'points[j]' は、現在のエッジ 'points[i]', Points[ (i 1) の外積 CP より小さいです。 % n]' と次の点 'point [(j 1) % n]' の後のエッジ。これにより、現在のエッジが次のエッジに対して垂直であることが検証されます。 現在の点

  'point[i]'
と次の点
• ' の間の距離まで、

  k を多角形内の次の点に移動します。距離 point[k]' は、現在のポイント 'point[i]' と次のポイント 'points[(k 1)%n]'# の間の距離より小さいです # ＃。これにより、次のポイントが現在のポイントから最も遠いことが確認されます。 今、点 j, k,

  と現在の点
'point[i]'
• の間の距離を計算し、これらすべての点を乗算します。

  result 変数の最大値を取得します。 main 関数を開始し、座標平面の値を

  "vector
point"
変数に適用します。

• 最後に、関数名 rotatingCaliper()

  を呼び出し、パラメータとして
'points'
• 値を渡し、回転キャリパー プロットの最大距離を取得します。

  ＃＃＃例＃＃＃ このプログラムでは、回転キャリパー法を使用して、座標平面内の 2 点間の最大距離を計算します。 リーリー ＃＃＃出力＃＃＃ リーリー ＃＃＃結論は＃＃＃

  2 つの座標点間の最大距離を計算することで、回転キャリパー法の概念を理解しました。この方法の実際の応用には、開口角の最適化、機械学習分類などが含まれます。

以上が回転キャリパー法を使用して、座標平面上の 2 点間の最大距離を計算します。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。