GPT-4は97回の対話を通じて地球規模の問題を調査し、P≠NPという結論に達する

科学研究の分野に携わっている人なら、多かれ少なかれ P/NP 問題について聞いたことがあるでしょう。この問題は、クレイ数学研究所によるミレニアム賞の問題に含まれていました。有名なポアンカレ予想やリーマン予想などの大きな問題。そしてこの組織は、問題を解決できる研究者に数百万ドルの賞金を提供しています。

P/NP 問題は、1971 年に Stephen A. Cook と Leonid Levin によってそれぞれ初めて提案されました。長年にわたり、多くの人がこの問題の研究に専念してきました。しかし、P=NP 問題を解決するには控えめに見積もっても 100 年かかるかもしれないと言う人もいます。

近年、P が次と等しいことを証明したと主張する人もいます。または NP に等しくありませんが、証明プロセスにエラーがあります。しかし、これまでのところ誰も明確な答えを与えることができていません。

人工知能技術の発展、特に過去 1 年間の大規模な言語モデルの急速な更新により、研究者たちは研究を始めています。人工知能テクノロジーを使用していくつかの世界的な問題を解決しようと試みます

Microsoft Research、北京大学、北杭大学、その他の機関の研究者は、大規模言語モデル (LLM) を使用して強化および加速することを提案しましたP 対 NP 問題の研究

この記事では、LLM に深く考えさせ、複雑な問題を解決するための一般的なフレームワークであるソクラテス的推論を提案します。このフレームワークに基づいて、LLM は問題を再帰的に発見、解決、統合すると同時に、自己評価と改善も行うことができます。

P 対 NP 問題に関するこの論文のパイロット研究GPT-4 は証明パターンの生成に成功し、97 回の対話ラウンドで厳密な推論を実行し、「P≠ NP」という結論に達したことを示しています。これは (Xu and Zhou, 2023) の結論と一致しています。

論文を表示するには、次のリンクをクリックしてください: https://arxiv.org/pdf/2309.05689.pdf

この記事の主な貢献は次のように要約できます:

• ## 人間との協力パートナーとして LLM を使用して、複雑な科学的課題に対処し、「LLM」を提案するfor Science (LLM4Science )」パラダイム。
• 「ソクラティック推論」と呼ばれるフレームワークを導入し、LLM が演繹、変換、分解、その他のモードを使用して批判的思考を刺激することを奨励します。
• GPT-4 とソクラテス推論フレームワークを使用してパイロット研究を実施し、理論コンピューター サイエンスにおける P 対 NP の問題を解決します。
• GPT-4 は証明パターンの生成に成功し、97 回の対話ターンで厳密な推論を実行し、P ≠ NP という結論に達しました。これは Xu and Zhou (2023 ) の最近の研究と一致しています。
• この研究は、GPT-4 のような LLM が人間と協力して新しい知識を推論し、専門家レベルの複雑な問題を探索する潜在的な能力を実証しています。
• この記事では、特定のタスクに合わせて調整されたこれまでの特化された AI モデルとは異なり、ドメイン全体にわたる一般的なイノベーション リーダーとしての LLM に焦点を当てます。
• LLM 自然言語と数学言語を流暢に使用できる能力は、学際的な発見に不可欠です。
• この研究では、さまざまな分野にわたる科学研究プロセスを強化および加速するパートナーとして LLM をどのように活用できるかを明らかにしています。

書き直された内容: この段落では、古代ギリシャの哲学者ソクラテスに触発されてフレームワークを「ソクラテス推論」と名付けたと述べています。ソクラテスはかつてこう言いました:「私は誰にも何も教えることはできません。私ができるのは彼らに考えさせることだけです。」フレームワークの全体的な設計思想は同じであり、LLM をさまざまな分野で使用できるようにする一般的な問題解決フレームワークです。幅広い解法空間をナビゲートし、効果的に答えに到達します。

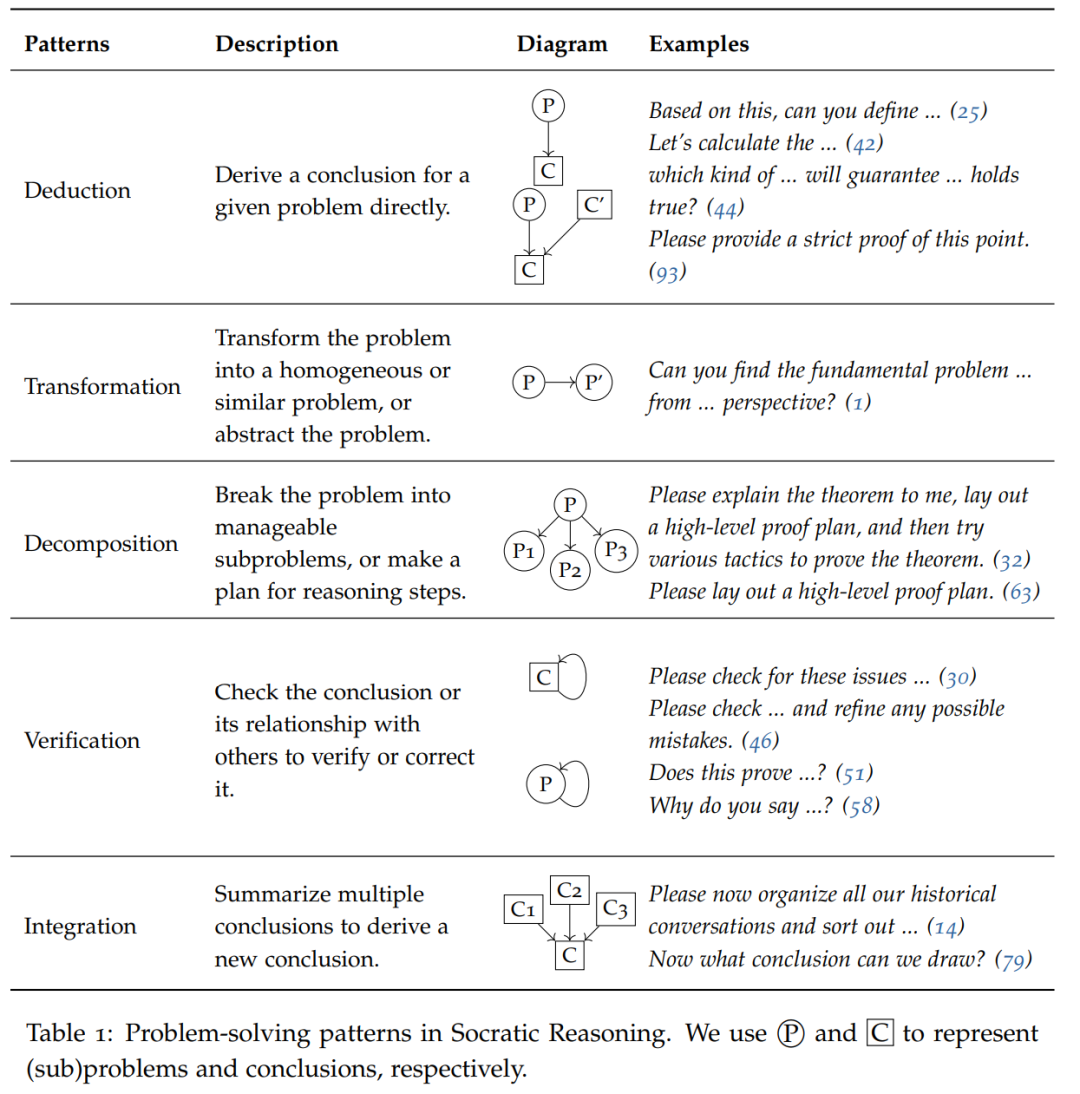
表 1 は、「ソクラテス推論」の 5 つのプロンプト モード (演繹、変換、分解、検証、融合) を示しています。これらのパターンは、新しい洞察や視点を発見し、複雑な問題をサブ質問や小さなステップに分割し、より小さな問題での答えに対する挑戦的な応答

によって自己改善に取り組むために使用されます (アトミックこのとき、LLM が直接結論を導くために、演繹的モード (たとえば、「ステップごとに考えさせます...」というプロンプト) が使用されます。

より複雑な問題の場合、この記事ではまず、LLM が問題を新しい問題に変換するか、いくつかの下位問題に分解する必要があります。これらのパターンは、アトミック ji 問題に到達するまで再帰的に実行されます。

新しい問題が発生したり、新しい結論が導き出された場合は、検証モードを採用し、LLM の自己評価機能を使用して検証および改善する必要があります。

最後に、融合モードでは、LLM がサブ問題の結果に基づいて結論を総合する必要があります。

一連の対話を通じて、LLM が再帰的に動機付けされて、問題を継続します。対象の問題が解決されるまで、上記のプロセスを繰り返します

この作品では、「ソクラテス的推論」は、難しい質問に対する体系的なプロンプト フレームワークを提供します

下の図は、「ソクラテス的推論」の P 対 NP 問題を解くために使用される対話の例です。ケーススタディでは GPT-4 API が使用されており、さらに記事ではラウンド インデックスに基づいてプロセスが分類されています。

#この記事では、探索の過程において、確率論に精通した数学者など、補助証明者としての 5 つの異なる役割を紹介します。実験では、対話前 14 ラウンドと後 83 ラウンドに分かれ、合計 97 ラウンドの対話が行われました。

たとえば、最初のラウンドのプロンプト: 「哲学的な観点から話せます」コンピュータ理論からではなく、P!=NP の観点から、P!=NP の背後にある根本的な問題を見つけることができるでしょうか?

#その他のヒントは次のとおりです:

対話は続き、最終ラウンドの対話は次のようになります。最終的に、P≠ NP

と結論付けられます。興味のある読者は、元の論文をチェックして詳細を確認してください。

以上がGPT-4は97回の対話を通じて地球規模の問題を調査し、P≠NPという結論に達するの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。