数字合わせゲーム？

Number Connect は、グリッド内の数字を接続するパスを見つけるロジック パズルです。

#Numberlink パズルの簡単な例 Numberlink パズルの解決策

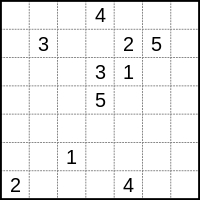
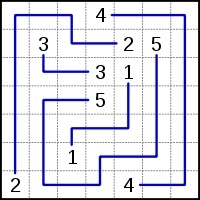
ルール - プレイヤーは次のことを行う必要があります。グリッド上の一致するすべての数値を 1 本の実線 (またはパス) で照合します。線が分岐したり交差したりすることはできず、数字は各線の末尾にある必要があります (つまり、真ん中ではありません)。 Numberlink 設計者の中にはこれを指定していない場合もありますが、問題が固有の解決策を持ち、グリッド内のすべてのセルが塗りつぶされている場合にのみ、問題は適切に設計されていると見なされます。

Game - ブロックの n×n 配列を考えてみましょう。いくつかの四角形は空であり、いくつかは実線であり、いくつかの非実線の四角形は整数 1、2、3、... でマークされています。各整数はボード上の 2 つの異なる正方形を占めます。プレイヤーのタスクは、水平方向と垂直方向の動きのみを使用して、ボード上の各整数の 2 つの出現を単純なパスで接続することです。 2 つの異なるパスが交差することはできません。どのパスにもソリッド ブロックを含めることはできません (どのパスにもソリッド ブロックは許可されません)。最後に、すべての非実線の正方形をパスで埋める必要があります。

アルゴリズム - ボード サイズ n×n の効率的なランダム パズルを準備するには、まずボード上にランダムで単純な素のパスを生成します。生成されたすべてのパスの外側に孤立したブロックがいくつか残っている場合は、これらの孤立したブロックをソリッド (禁止) としてマークします。次に、パスの終点と塗りつぶされた正方形のリストをパズルとして使用します。

したがって、最初に解を生成し、次にその解からパズルを解きます。パスと実線の四角形は、n×n のチェス盤を複数の部分に分割します。この分割を生成するには、union-lookup データ構造を使用します。このデータ構造は、チェス盤上の n^2 マスのサブセットを処理します。

説明

• 次のようなチェス盤上の正方形 (i, j) と (k, l) をランダムに見つけます: (a) (i, j) および (k) 、l) は互いに隣接しており、(b) (i, j) も (k, l) もこれまでに生成されたパスに属しません。ボード全体でそのような正方形のペアが見つからない場合は、失敗が返されます。 /* ここで、(i, j) と (k, l) は、構築される新しいパスの最初の 2 つの正方形です。 *

• (i, j) と (k, l) を含む 2 つの共用体検索ツリーをマージします。

• 現在のパスを拡張できなくなるまで、次の手順を繰り返します。 (i, j) の名前を (k, l) に変更します。 (a) (k, l) は、これまでに生成されたパス (現在のパスを含む) に属さない (b) 構築された現在のパス上一部 (i, j の唯一の近傍) は (k, l) です。

• そのような隣接する正方形 (k, l) が見つからない場合、パスをこれ以上拡張することはできないため、ループが飛び出すことになります。それ以外の場合は、(i, j) と (k, l) を含む 2 つの共用体検索ツリーをマージします。

• 新しいパスの開始ブロックと終了ブロックのフラグを設定します。

#正常に戻りました
• 入力

  | || || || || || || 4 |
  | || || || || || 3 || |
  | || || 2 || 2 || || || 3 |
  | || || || || X || || 1 |
  | || || 6 || || || 7 || 7 |
  | 5 || 4 || || X || || X || 1 |
  | || 5 || || 6 || || || |

出力

上記の表の解決策

| 4 || 4 || 4 || 4 || 4 || 4 || 4 |
| 4 || 1 || 1 || 1 || 1 || 3 || 3 |
| 4 || 1 || 2 || 2 || 1 || 1 || 3 |
| 4 || 1 || 1 || 1 || X || 1 || 1 |
| 4 || 4 || 6 || 1 || 1 || 7 || 7 |
| 5 || 4 || 6 || X || 1 || X || 1 |
| 5 || 5 || 6 || 6 || 1 || 1 || 1 |

Example

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
struct _node {
   struct _node *parent;
   int rank;
   int path_number;
   int endpoint;
};
typedef struct _node node;
/* Name: initboard()
Input: 2D-array of pointers, size of array row/column
Output: --void--
Description: Takes a table of pointers and initializes it. */
void initboard(node ***arr, int n) {
   int i, j;
   for (i=0;i<n;i++){
      for (j=0;j<n;j++){
         node *np;
         np = (node *)malloc(sizeof(node));
         np->rank = 0;
         np->parent = NULL;
         np->path_number = 0;
         np->endpoint = 0;
         arr[i][j] = np;
      }
   }
}
/*

Input:a node
Output:the set pointer of the set the node belongs to

説明

- ノードを取得し、ポインタを設定します。 */

node *findset(node *n) {
   if (n->parent != NULL)
      n = n->parent;
   return n;
}
void setunion(node *x, node *y) {
   x = findset(x);
   y = findset(y);
   if (x->rank > y->rank)
      y->parent = x;
   else {
      x->parent = y;
      if(x->rank == y->rank)
         y->rank++;
   }
}
int neighbour(int n, node ***arr) {
   int i1, i2, j1, j2, ct = 0, flag = 0, a, b,k2;
   int k = rand()%(n*n);
   while (ct < (n*n)) {
      k %= (n*n);
      i1 = k/n;
      j1 = k%n;
      if (arr[i1][j1]->path_number==0) {
         int kk = rand()%4;
         int cc = 0;
         switch (kk) {
            case 0: i2= i1-1;
               j2= j1-0;
            if(i2>=0 && i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 1: i2= i1-0;
               j2= j1-1;
            if(j2>=0 && i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 2: i2= i1+1;
            j2= j1-0;
            if(i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 3: i2= i1-0;
            j2= j1+1;
            if(i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 4: if(cc==4)
               break;
            i2= i1-1;
            j2= j1-0;
            if(i2>=0 && i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 5: if(cc==4)
               break;
            i2= i1-0;
            j2= j1-1;
            if(j2>=0 && i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 6: if(cc==4)
               break;
            i2= i1+1;
            j2= j1-0;
            if(i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 7: if(cc==4)
               break;
            i2= i1-0;
            j2= j1+1;
            if(i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
         }
      }
      if(flag==1)
         break;
         ct++;
         k++;
   }
   if(ct<n*n) {
      k2= (i2*n)+j2;
      return k*(n*n)+k2;
   } else {
      return -1;
   }
}
int checkneigh(int k1, int k2, int n, node ***arr) {
   int i= k2/n;
   int j= k2%n;
   int ii= k1/n;
   int jj= k1%n;
   int ct=0;
   if(i>0 && findset(arr[i-1][j])==findset(arr[ii][jj]))
      ct++;
   if(i<n-1 && findset(arr[i+1][j])==findset(arr[ii][jj]))
      ct++;
   if(j>0 && findset(arr[i][j-1])==findset(arr[ii][jj]))
      ct++;
   if(j<n-1 && findset(arr[i][j+1])==findset(arr[ii][jj]))
      ct++;
   if(ct>1)
      return 0;
   else
      return 1;
}
int valid_next(int k, int n, node ***arr) {
   int i1, i2, j1, j2, a, b, kk, stat,ct=0;
   int flag=0;
   i1= k/n;
   j1= k%n;
   kk= rand()%4;
   switch(kk) {
      case 0: i2= i1-1;
         j2= j1-0;
      if(i2>=0 && i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 1: i2= i1-0;
         j2= j1-1;
      if(j2>=0 && i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 2: i2= i1+1;
         j2= j1-0;
      if(i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 3: i2= i1-0;
         j2= j1+1;
      if(i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 4: if(ct==4)
         break;
      i2= i1-1;
      j2= j1-0;
      if(i2>=0 && i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 5: if(ct==4)
         break;
      i2= i1-0;
      j2= j1-1;
      if(j2>=0 && i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 6: if(ct==4)
         break;
      i2= i1+1;
      j2= j1-0;
      if(i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 7: if(ct==4)
         break;
      i2= i1-0;
      j2= j1+1;
      if(i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
   }
   //printf("flag- %d</p><p>",flag);
   if(flag==0)
      return -1;
   if(flag) {
      //printf("value sent- %d</p><p>", i2*n + j2);
      return (i2*n)+j2;
   }
}
int addpath(node ***arr, int n, int ptno) {
   int a,b,k1,k2;
   int i1,j1,i2,j2;
   k2= neighbour( n, arr);
   if(k2==-1) //no valid pair found to start with
      return 0;
   k1= k2/(n*n);
   k2= k2%(n*n);
   //printf("%d %d</p><p>",k1,k2);
   i1= k1/n;
   j1= k1%n;
   i2= k2/n;
   j2= k2%n;
   arr[i1][j1]->endpoint= 1;
   arr[i2][j2]->path_number= ptno;
   arr[i1][j1]->path_number= ptno;
   node *n1, *n2;
   n1= arr[i1][j1];
   n2= arr[i2][j2];
   n1= findset(n1);
   n2= findset(n2);
   setunion(n1, n2);
   while(1) {
      i1= i2;
      j1= j2;
      k1= (i1*n)+j1;
      k2= valid_next(k1,n,arr);
      if(k2==-1) {
         arr[i1][j1]->endpoint= 1;
         break;
      }
      i2=k2/n;
      j2=k2%n;
      arr[i2][j2]->path_number= ptno;
      node *n1, *n2;
      n1= arr[i1][j1];
      n2= arr[i2][j2];
      n1= findset(n1);
      n2= findset(n2);
      setunion(n1,n2);
   }
   return 1;
}
void printtable(node ***arr, int n) {
   int i,j;
   printf("Table to be solved:</p><p>");
   for(i=0;i<n;i++) {
      for(j=0;j<n;j++) {
         if(arr[i][j]->endpoint ==1){
            if(arr[i][j]->path_number/10==0)
               printf("| %d |",arr[i][j]->path_number);
            else
               printf("| %d|",arr[i][j]->path_number);
         } else if(arr[i][j]->path_number==0)
            printf("| X |");
         else
            printf("| |");
      }
      printf("</p><p>");
   }
   printf("</p><p></p><p>The solution to the above table:</p><p>");
   for(i=0;i<n;i++) {
      for(j=0;j<n;j++) {
         if(arr[i][j]->path_number != 0){
            if(arr[i][j]->path_number/10==0)
               printf("| %d |",arr[i][j]->path_number);
            else
               printf("| %d|",arr[i][j]->path_number);
         } else
            printf("| X |");
      }
      printf("</p><p>");
   }
}
int main(void) {
   srand((unsigned int) time (NULL));
   int i, j;
   int ct = 1;
   int n = 7;
   node*** pointers= (node ***)malloc(n*sizeof(node **));
   for (i=0; i<n; i++)
      pointers[i] = (node **)malloc(n*sizeof(node *));
   initboard(pointers, n);
   while(1) {
      i = addpath(pointers, n, ct);
      if (i==0) {
         break;
      } else {
         ct++;
      }
   }
   printtable(pointers,n);
   return 0;
}

以上が数字合わせゲーム？の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。