指定された二分探索ツリー内のより大きな値をすべて各ノードに追加します

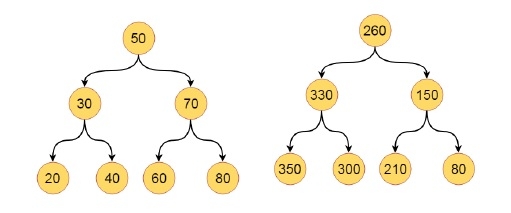
ここで興味深い問題がわかります。指定された二分探索ツリーの各ノードに、より大きな値を追加します。最初と最後のツリーは次のようになります -

##Algorithm

bstUpdate(root, sum) -

Begin
   if root is null, then stop
   bstUpdate(right of room, sum)
   sum := sum + value of root
   update root value using sum
   bstUpdate(left of room, sum)
End

例

#include<iostream>
using namespace std;
class Node {
   public:
      int data;
      Node *left, *right;
   };
   Node *getNode(int item) {
      Node *newNode = new Node();
      newNode->data = item;
      newNode->left = newNode->right = NULL;
      return newNode;
}
void updateBST(Node *root, int *sum) {
   if (root == NULL)
      return;
   updateBST(root->right, sum); //update right sub tree
   *sum = *sum + root->data;
   root->data = *sum; //update root data
   updateBST(root->left, sum); //update left sub tree
}
void BSTUpdate(Node *root) {
   int sum = 0;
   updateBST(root, &sum);
}
void inorder(Node *root) {
   if (root != NULL) {
      inorder(root->left);
      cout<<root->data<<" ";
      inorder(root->right);
   }
}
Node* insert(Node* node, int data) {
   if (node == NULL)
      return getNode(data);
   if (data <= node->data) //go to left
      node->left = insert(node->left, data);
   else //go to right
      node->right = insert(node->right, data);
   return node;
}
int main() {
   int data[] = {50, 30, 20, 40, 70, 60, 80};
   int n = sizeof(data)/sizeof(data[0]);
   Node *root = NULL;
   for(int i = 0; i < n; i++) {
      root = insert(root, data[i]);
   }
   BSTUpdate(root);
   inorder(root);
}

出力

350 330 300 260 210 150 80

以上が指定された二分探索ツリー内のより大きな値をすべて各ノードに追加しますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。